Definizioni statistiche >Modo Pearson Skewness
Il modo Pearson skewness, chiamato anche primo coefficiente di skewness di Pearson, è un modo per capire la skewness di una distribuzione.
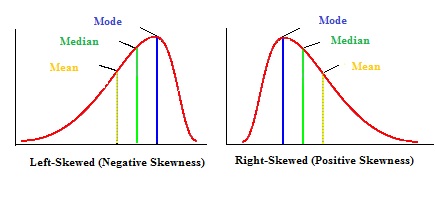
La media, il modo e la mediana possono essere usati per capire se si ha una distribuzione inclinata positivamente o negativamente.
- Se la media è maggiore della modalità, la distribuzione è inclinata positivamente.
- Se la media è minore della modalità, la distribuzione è inclinata negativamente.
- Se la media è maggiore della mediana, la distribuzione è inclinata positivamente.
- Se la media è minore della mediana, la distribuzione è inclinata negativamente.
Il modo Pearson di skewness
Il modo Pearson di skewness usa i fatti di cui sopra per aiutarvi a scoprire se avete uno skewness positivo o negativo. Se avete una distribuzione e conoscete la media, la modalità e la deviazione standard (σ), allora la formula della Pearson mode skewness è:
(media-modalità)/σ
Problema del campione: avete dati con una media di 19, una modalità di 20 e una deviazione standard di 25. Cosa ti dice la Pearson Mode Skewness sulla distribuzione?
(media-modalità)/σ = (19-20)/25 = -0.04.
C’è una leggerissima asimmetria negativa (-0.04). Nota: per la maggior parte degli intenti e degli scopi, questa conterebbe come una distribuzione simmetrica poiché l’asimmetria è così piccola.
Skewness del modo di Pearson: Formula alternativa.
Se non conoscete la modalità, non sarete in grado di usare l’asimmetria di Pearson. Tuttavia, la direzione dell’asimmetria può essere calcolata anche trovando dove sono la media e la mediana. Secondo Business Statistics, questo porta a una seconda formula equivalente:
3(Media – Mediana) / σ
Questa formula è anche chiamata secondo coefficiente di asimmetria di Pearson: Cosa significano i risultati.
La differenza tra la media e la modalità, o media e mediana, vi dirà quanto la distribuzione si allontana dalla simmetria. Una distribuzione simmetrica (per esempio, la distribuzione normale) ha un’asimmetria pari a zero.
Entrambe le equazioni danno risultati in deviazioni standard, che sono unità di misura senza dimensione dalla media.
Dodge, Y. (2008). L’enciclopedia concisa della statistica. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Klein, G. (2013). L’introduzione a fumetti alla statistica. Hill & Wamg.
Vogt, W.P. (2005). Dizionario di Statistica &Metodologia: A Nontechnical Guide for the Social Sciences. SAGE.
Stephanie Glen. “Pearson Mode Skewness” da StatisticsHowTo.com: Statistica elementare per il resto di noi! https://www.statisticshowto.com/pearson-mode-skewness/
——————————————————————————
Hai bisogno di aiuto per un compito a casa o per un test? Con Chegg Study, puoi ottenere soluzioni passo dopo passo alle tue domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!