Prima di iniziare dobbiamo fare alcuni presupposti.
In primo luogo, stiamo lavorando con fluidi newtoniani. Questo è il modo matematico più semplice per rendere conto della viscosità in un fluido. Non ci sono fluidi reali che rientrano perfettamente in questa categoria, ma nella maggior parte dei casi, l’aria e l’acqua possono essere trattati come un fluido newtoniano. L’altra ipotesi molto importante che facciamo è che il fluido sia incomprimibile. Questo significa che la sua densità, rho, è una costante.
Conservazione della massa

La prima equazione ci dice che la massa del fluido su cui stiamo lavorando si conserva. Il fluido può cambiare la sua forma ma questa equazione ci dice che la massa è la stessa dall’inizio alla fine.
Ora parliamo di matematica. La lettera u rappresenta la velocità del fluido ed è un vettore. Ha tre componenti, possiamo chiamarle u, v, w e rappresentano la velocità del fluido nelle direzioni x, y e z. La lettera greca nabla ∇ seguita da un punto è l’operatore di divergenza. Questo significa che dobbiamo differenziare le sue componenti in ogni direzione (in questo caso x, y, z).

La prima derivata ci dice come cambia la componente x della velocità mentre ci spostiamo nella direzione x. Lo stesso vale per le altre due derivate. Poiché questa equazione è uguale a zero, ci mostra che la massa è conservata.
Conservazione della quantità di moto

La seconda equazione è in realtà un insieme di tre equazioni differenziali. Questa è quella che può essere descritta come la seconda legge di Newton per i fluidi. Se espandiamo l’espressione otteniamo un sistema complesso.
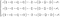
Siccome è molto più semplice da capire, ci concentreremo sulla conservazione della quantità di moto non espansa.
Quando lavoriamo con i fluidi possiamo dire che la massa e la densità sono la stessa cosa (purché il loro volume sia lo stesso). Se stiamo considerando due fluidi, possiamo dire che quello più denso è quello più “pesante” (ad esempio, mercurio e acqua). In questo caso, la lettera greca ρ (rho) è la densità del fluido.
Abbiamo la massa, ora per tornare alla seconda legge di Newton ci serve l’accelerazione. Che è esattamente il risultato della derivata temporale del vettore velocità.

Ora ci restano solo i termini a destra del segno di uguale, e quelli rappresentano tutte le forze che sono applicate al fluido.
Il primo termine ∇p è il gradiente della pressione. Rappresenta la differenza di pressione nello spazio in cui è contenuto il fluido. Per esempio, se c’è una zona con bassa pressione e un’altra con una pressione più alta, il fluido si sposterà dalla sezione ad alta pressione a quella più bassa. Il gradiente di p dice tutto questo.
Il secondo termine descrive la viscosità del fluido. Pensate a due liquidi diversi, come l’acqua e il miele. Quando versate un bicchiere d’acqua, questo cade rapidamente e facilmente. Quando fai la stessa cosa con il miele è appiccicoso e si versa molto lentamente. Questo è ciò che dice questa espressione.
L’ultimo termine, F, è il più semplice perché rappresenta tutte le forze esterne che possono essere applicate a quel fluido. Di solito, la forza che consideriamo qui è la gravità.
Ecco, tutti quei simboli e lettere fantasiose significano solo forza = massa x accelerazione.
Uso delle equazioni di Navier-Stokes
Siccome risolvere queste equazioni è così complicato, per usarle dobbiamo fare molte approssimazioni. Alcuni esempi sono il flusso di Poiseuille e Couette. Con un sacco di supposizioni, questi due scienziati sono stati in grado di trovare una soluzione alle equazioni di Navier-Stokes per un’applicazione molto specifica. Tuttavia, se vogliamo usarle per un compito più complicato, come le previsioni del tempo, dobbiamo fare qualcos’altro.
Il modo più comune di usare queste equazioni è trasformarle, con la media di Reynolds. Questo è un processo matematico avanzato e i risultati sono le equazioni di Reynolds. Di solito sono chiamate equazioni RANS (che significa equazioni di Navier-Stokes mediate da Reynolds).
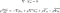
Queste equazioni sono usate quando il fluido è in un flusso turbolento. Assomigliano quasi esattamente alle equazioni di Navier-Stokes, tranne che per l’ultimo termine. Questo è chiamato tensore di stress di Reynolds. È la quantità che ci permette di tenere conto della turbolenza nel fluido.
Nelle equazioni RANS, le quantità che usiamo sono mediate su un intervallo di tempo. Questo intervallo deve essere abbastanza piccolo da permettere l’osservazione del fenomeno che stiamo studiando. Allo stesso tempo, deve essere abbastanza grande da far perdere importanza all’effetto della turbolenza.
Con i giusti presupposti, queste equazioni funzionano. Sappiamo come usarle per rendere le auto di F1 più veloci, per far andare un veicolo spaziale sulla ISS e per fare le previsioni del tempo. Quindi vi starete chiedendo perché la prova di queste equazioni vale un milione di dollari?
Un premio da un milione di dollari
Dal punto di vista della fisica, queste equazioni sono solo la seconda legge di Newton che funziona con i fluidi. Quando facciamo alcune ipotesi e alcune semplificazioni, possiamo fare cose sorprendenti con esse.
Il vero problema è questo. Risolvere queste equazioni senza approssimazioni è terribilmente complicato. È così difficile che non è stato dimostrato che le soluzioni esistano davvero. Ed è qui che entra in gioco il Millennium Prize.
La dichiarazione ufficiale del problema (la trovate qui) è:
Provare o dare un controesempio della seguente affermazione: in tre dimensioni spaziali e temporali, dato un campo di velocità iniziale, esistono un vettore velocità e un campo di pressione scalare, entrambi lisci e globalmente definiti, che risolvono le equazioni di Navier-Stokes.
Questo significa che per vincere il premio bisogna fare tre cose:
- Provare che esiste una soluzione
- La soluzione deve esistere in ogni punto dello spazio
- La soluzione deve essere regolare. Questo significa che un piccolo cambiamento nelle condizioni iniziali produce solo una piccola variazione del risultato.
Per un ingegnere di solito è sufficiente sapere che queste equazioni funzionano, anche se solo a qualche livello di approssimazione. Tuttavia, per un matematico è molto importante sapere se le soluzioni esistono e come si comportano.
Potreste ora pensare che se funzionano così come sono, spendere tempo ed energie per cercare una dimostrazione è una totale perdita di tempo. Beh, come molti progressi tecnologici nella storia dell’umanità, il risultato può non sembrare molto importante. Ciò che è importante è il percorso per arrivarci, che può portare nuove conoscenze e miglioramenti alla nostra vita.
Pensate alle missioni spaziali. Se l’uomo non avesse mai deciso di andare a camminare sulla luna, non avremmo molti oggetti che servono a migliorare la nostra vita. Le macchine per la risonanza magnetica e i pacemaker provengono da tecnologie sviluppate per l’esplorazione spaziale. Oggi i medici di tutto il mondo li usano ogni giorno per salvare vite. La stessa cosa si applica qui. Il percorso per scoprire la soluzione delle equazioni di Navier-Stokes ci aiuterà a migliorare la nostra comprensione dei fluidi e non solo. Può portarci a nuove scoperte e probabilmente richiederà l’invenzione di nuova matematica. Questa potrà poi essere usata per rispondere a molti altri problemi, per inventare nuove tecnologie per migliorare la nostra vita e renderci migliori.