Se ti piace bere, la bottiglia di Klein non è un recipiente raccomandabile. Può sembrare vagamente una bottiglia, ma non racchiude alcun volume, il che significa che non può effettivamente contenere alcun liquido. Qualunque cosa si versi “dentro” tornerà fuori di nuovo.
Come si costruisce una cosa così strana e perché si vorrebbe costruirla? Il matematico Felix Klein, che scoprì la bottiglia nel 1882, la descrisse come una superficie che “può essere visualizzata invertendo un pezzo di un tubo di gomma e facendolo passare attraverso se stesso in modo che esterno e interno si incontrino”.
Il tuo browser non supporta il tag video.Direct link
È ovvio che la bottiglia di Klein, proprio come la più familiare sfera, è una superficie chiusa: è finita nel senso che la si può inserire in una regione finita di spazio, ma una formica potrebbe camminarci sopra all’infinito senza mai incontrare un confine o cadere oltre un bordo. A differenza della sfera, che ha un interno e un esterno, la bottiglia di Klein è unilaterale: camminando, la nostra formica potrebbe raggiungere entrambi i lati di ogni punto della superficie. Questo è il motivo per cui la bottiglia non racchiude alcun volume, e risponde anche alla domanda “perché”: la bottiglia di Klein è interessante perché non incontriamo molte forme unilaterali in natura. (Vedi qui per un’altra immagine molto bella di una bottiglia di Klein.)

Il nastro di Möbius è unilaterale – guarda la versione animata. (Immagine e animazione di Konrad Polthier.)
Se questo è un po’ confuso, pensate a un esempio più semplice di superficie unilaterale: il famoso nastro di Möbius. Si può fare prendendo due estremità di una striscia di carta, dando alla striscia una torsione, e poi incollando le estremità insieme. Usando una striscia di carta i cui due lati hanno colori diversi, per esempio verde e arancione, è facile convincersi che il nastro di Möbius risultante è unilaterale. Una volta che hai attorcigliato e incollato, scoprirai che puoi raggiungere ogni punto arancione da ogni punto verde senza dover perforare la carta o scavalcare il suo bordo.
A differenza della bottiglia di Klein, il nastro di Möbius ha un confine – è costituito dai due bordi non incollati della striscia originale. Ma c’è un legame tra i due. Se si prendono due strisce di Möbius e si crea una forma chiusa unendo i loro confini usando una normale striscia a due lati, come mostrato sotto, ciò che si ottiene è esattamente la bottiglia di Klein.
Il tuo browser non supporta il tag video.Direct link
i cui lati posteriore e anteriore sono colorati rispettivamente in bianco e blu. Animazione di Konrad Polthier.
Questo fatto ispirò il matematico Leo Moser a comporre un limerick:
Un matematico chiamato KleinPensava che la banda di Möbius fosse divina.Disse: “Se incolli i bordi di due, otterrai una strana bottiglia come la mia.”
Alcuni matematici sono davvero multi-talenti!
Un’altra curiosa caratteristica della bottiglia di Klein è che si interseca da sola, il che significa che è difficile realizzarla da un singolo tubo di gomma come Klein ha suggerito. In senso stretto, l’oggetto auto-intersecante raffigurato sopra non è una bottiglia di Klein, ma (come indicato da Klein) solo una visualizzazione di una bottiglia. Per capire perché, pensate prima alla più familiare ciambella (nota matematicamente come toro). Si può fare un toro da un foglio quadrato di gomma incollando prima due lati opposti per formare un cilindro, e poi incollando le due componenti limite di quel cilindro per ottenere il toro.

Fare un toro: Prima incollate punti opposti su due lati opposti del quadrato per fare un cilindro e poi incollate i due cerchi di confine di quel cilindro (corrispondenti all’incollaggio di punti opposti sui due lati rimanenti del quadrato) per formare un toro.
Se non volete preoccuparvi dell’incollaggio, potete semplicemente pensare al toro come a un quadrato, tenendo presente che punti opposti su lati opposti sono considerati uguali. Quindi quando fai scorrere una forma disegnata sul “quadrato” attraverso il bordo superiore, riapparirà sul bordo inferiore e quando la fai scorrere sul bordo destro riapparirà sul bordo sinistro (e viceversa).
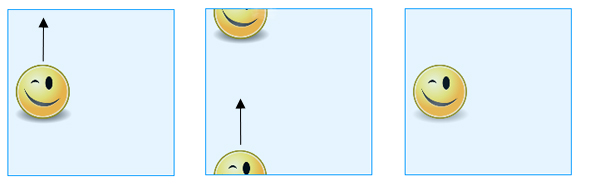
Quando fai scorrere una forma disegnata sul “quadrato” attraverso il bordo superiore, riapparirà sul bordo inferiore.
Per ottenere una vera bottiglia di Klein, inizia allo stesso modo, identificando punti opposti su una coppia di lati opposti di un quadrato. Per l’altra coppia di lati, però, non individuare punti direttamente opposti, ma punti diagonalmente opposti, come mostrato in figura.
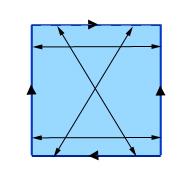
Facendo una bottiglia di Klein: individua i punti opposti di due lati opposti (quelli verticali in questa figura) e poi individua i punti diagonalmente opposti sui due lati rimanenti. (Se etichettate i punti sui lati superiore e inferiore da sinistra a destra con i numeri da 0 a 1, allora un punto con etichetta x sul lato superiore è identificato con il punto con etichetta 1-x sul lato inferiore.)
L’oggetto risultante è la bottiglia di Klein. Di nuovo, puoi pensarla come un quadrato, tenendo presente quali punti di confine sono considerati uguali. Se si fa scorrere una forma su uno dei bordi che aveva punti opposti identificati (verticale nella nostra immagine), essa riappare sul lato opposto, come prima. Se, invece, la fai scorrere su uno dei bordi i cui punti sono stati identificati in diagonale (orizzontale nella nostra immagine), essa riappare sul lato opposto, ma spostata e come immagine speculare del suo sé originale.
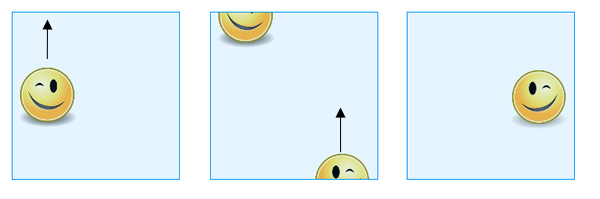
Se si fa scorrere una forma sul bordo superiore, essa appare attraverso il bordo inferiore, ma dall’altra parte e come un’immagine speculare del suo sé originale.
L’unico modo per costruire questa forma nello spazio tridimensionale incollando effettivamente i punti insieme è quello di permetterle di intersecarsi. Questo equivale a identificare coppie di punti all’interno del quadrato originale, quindi a rigore la forma risultante non è esattamente la stessa della bottiglia di Klein, che ha solo punti di confine identificati. È solo un modo di rappresentare la bottiglia nello spazio tridimensionale (ce ne sono anche altri).
Il tuo browser non supporta il tag video.Link diretto
Immagine speculare e orientabilità. Animazione di Konrad Polthier.
Curiosamente, i concetti di “dentro”, “fuori” e “unilateralità” dipendono dallo spazio ambientale in cui si trova un oggetto. Per esempio, un loop disegnato su un pezzo di carta (in uno spazio bidimensionale) ha un interno e un esterno ben definiti, ma un loop disegnato nello spazio tridimensionale no. Questo è il motivo per cui non possiamo parlare di unilateralità se prima non decidiamo come incorporare una superficie nello spazio tridimensionale. C’è, tuttavia, una proprietà strettamente correlata che è intrinseca a una forma e non dipende dallo spazio circostante. Una superficie è detta orientabile se non è possibile far scorrere una forma disegnata su di essa intorno e tornare al punto di partenza in modo che appaia come la sua stessa immagine speculare. Come potete vedere nell’animazione che accompagna l’immagine a destra, il nastro di Möbius non è orientabile. E come puoi vedere dall’immagine con la faccina sorridente qui sopra, nemmeno la bottiglia di Klein lo è. Per darne una descrizione matematica completa, la bottiglia di Klein è una superficie chiusa e non orientabile. Per saperne di più vedi l’articolo Dentro la bottiglia di Klein.
Informazioni sull’autore
Marianne Freiberger è redattrice di Plus.