Costruire un triangolo equilatero – MathBitsNotebook (Geo

Triangolo equilatero MathBitsNotebook.com Schema Topico | Schema di Geometria | MathBits’ Teacher Resources Termini di utilizzo Persona di contatto: Donna Roberts

Usa solo il compasso e la riga quando disegni una costruzione. Non disegnare a mano libera!

Faremo TRE costruzioni di un triangolo equilatero. La prima sarà costruire un triangolo equilatero data la lunghezza di un lato, e le altre due saranno costruire un triangolo equilatero inscritto in un cerchio.

Data: la lunghezza di un lato del triangolo Costruisci: un triangolo equilatero

PS:
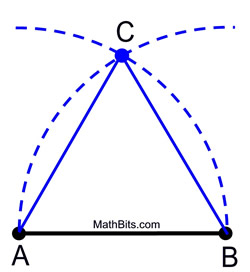
1. Posizionare il punto del compasso su A e misurare la distanza dal punto B. Far oscillare un arco di queste dimensioni sopra (o sotto) il segmento.
2. Senza cambiare l’arco sul compasso, posizionare il punto del compasso su B e far oscillare lo stesso arco, intersecando il primo arco.
3. Etichettare il punto di intersezione come terzo vertice del triangolo equilatero.

Vedere i cerchi completi al lavoro.

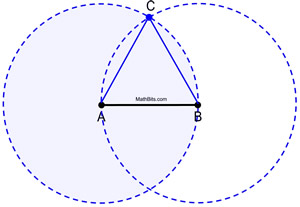Prova della costruzione: Il cerchio A è congruente al cerchio B, dal momento che sono stati formati usando la stessa lunghezza di raggio, AB. Poiché AB e AC sono lunghezze di raggi del cerchio A, sono uguali tra loro. Allo stesso modo, AB e BC sono raggi del cerchio B e sono uguali tra loro. Pertanto, AB = AC = BC per sostituzione (o proprietà transitiva). Poiché i segmenti congruenti hanno lunghezze uguali, e ΔABC è equilatero (avendo tre lati congruenti).

PS:
1. Posiziona la punta del tuo compasso sul foglio e disegna un cerchio. (Mantenere questa spanna di compasso!)
2. Mettere un punto, etichettato A, in qualsiasi punto della circonferenza del cerchio per agire come punto di partenza.
3. Senza cambiare la portata del compasso, mettete il punto del compasso su A e fate un piccolo arco che attraversa la circonferenza del cerchio.
4. Senza cambiare la portata del compasso, spostate il punto del compasso all’intersezione dell’arco precedente con la circonferenza e fate un altro piccolo arco sulla circonferenza del cerchio.
5. Continua a ripetere questo processo di “passo” intorno al cerchio fino a tornare al punto A.
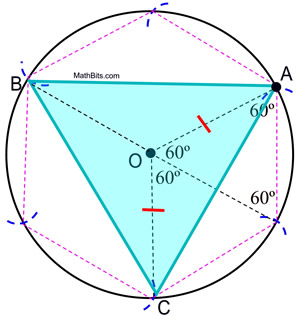
6. Partendo da A, collega ogni altro arco sul cerchio per formare il triangolo equilatero.

Fare riferimento alla dimostrazione di un esagono regolare inscritto per ulteriori informazioni relative alla dimostrazione di questa costruzione.

Prova della costruzione: La dimostrazione dell’esagono regolare inscritto mostra che gli angoli centrali di un esagono regolare contengono 60º. Gli angoli centrali del triangolo inscritto in questo cerchio contengono 120º. Poiché ΔAOC è isoscele (OA e OC sono lunghezze di raggio), m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC ΔCOB ΔBOA per SAS. Per CPCTC, ∠OCB ∠OCA e m∠OCB = 30º per sostituzione e m∠BCA = 60º. In modo simile, abbiamo m∠ACB = m∠CBA = m∠BAC = 60º e ΔABC equilatero.

PASSI:
1. Posizionare la punta del compasso sul foglio e disegnare un cerchio, O. (Mantenere questa spanna del compasso!)
2. Usando un righello, disegnare un diametro del cerchio, etichettando i punti finali P e B.
3. Senza cambiare la spanna del compasso, posizionare la punta del compasso su P e disegnare un cerchio completo.
4. Etichettare i punti di intersezione delle due circonferenze del cerchio con A e C.
5. Disegnare i segmenti da A a B, da B a C e da C ad A, per formare il triangolo equilatero.

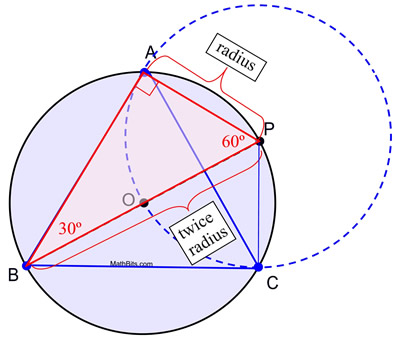
Prova della costruzione: Questa costruzione utilizza il fatto che un angolo inscritto in un semicerchio è un angolo retto, e che in un triangolo 30º-60º-90º, la lunghezza della gamba corta è la metà della lunghezza dell’ipotenusa. In questa costruzione, il cerchio O e il cerchio P sono congruenti poiché hanno lo stesso raggio. AP è una lunghezza di raggio del cerchio P e il raggio AP = OP. OP è anche una lunghezza di raggio del cerchio O (insieme a OB) e il diametro BP = BO + OP = 2 OP. Per sostituzione, BP = 2 AP, creando le condizioni necessarie per m∠ABP = 30º. Di conseguenza, m∠APB = 60º. Un argomento simile può essere usato per stabilire che per ΔPBC, m∠PBC = 30º e m∠BPC = 60º rendendo ΔPBC ΔPBA per ASA (con lato condiviso da B a P).
Ora, poiché sono i lati corrispondenti dei due triangoli congruenti, rendendo ΔABC isoscele. ∠BAC ∠BCA poiché gli angoli di base di un triangolo isoscele sono congruenti.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º per postulato di addizione degli angoli e sostituzione. m∠BAC + m∠BCA + m∠ABC = 180º perché la somma delle misure degli angoli in un triangolo è 180º. Poiché m∠BAC + m∠BAC + 60º = 180º per sostituzione, sappiamo che 2m∠BAC = 120º e m∠BAC = 60º. Di conseguenza, anche m∠BCA è uguale a 60º per sostituzione, rendendo ΔABC equilatero.