Qual è la permeabilità della membrana cellulare?
Modalità lettore
Una delle caratteristiche distintive di tutti gli organismi viventi è quella di contenere una particolare miscela di ioni e piccole molecole. La composizione non solo differisce dall’ambiente, ma può anche variare all’interno della cellula. Per esempio, la concentrazione di ioni idrogeno in alcuni compartimenti cellulari può essere 104 volte maggiore che in altri (i mitocondri raggiungono un pH fino a 8; i lisosomi un pH fino a 4, BNID 107521, 106074). Il rapporto tra le concentrazioni di ioni Ca2+ nei compartimenti fluidi extra e intracellulari può essere ancora una volta di 104 volte (BNID 104083). Questa differenza di concentrazione è così grande che il trasporto di uno ione Ca2+ attraverso la membrana, dal compartimento intra- a quello extracellulare, richiede l’energia di più di un protone o di uno ione sodio che scorre lungo il gradiente di forza protonica. Per vedere questo, il lettore dovrebbe ricordare la regola empirica della nostra lista di trucchi del mestiere che per stabilire una differenza di potenziale di un ordine di grandezza richiede 6 kJ/mol (≈2 kBT). Questa energia può essere ottenuta per esempio trasportando una carica elettrica attraverso una differenza di potenziale di 60 mV. Per ottenere un rapporto di concentrazione di quattro ordini di grandezza richiederebbe quindi il trasporto di una carica attraverso circa 240 mV di forza motrice degli elettroni (in realtà anche di più a causa della doppia carica dello ione calcio). Questo è molto vicino alla tensione di rottura della membrana come discusso nella vignetta su “Cos’è la differenza di potenziale elettrico attraverso le membrane? Infatti l’alto rapporto di concentrazione di Ca2+ è solitamente ottenuto accoppiandosi al trasporto di tre ioni sodio o all’idrolisi dell’ATP, che aiuta a raggiungere la differenza di densità richiesta senza eccitare pericolosamente la membrana.
La seconda legge della termodinamica ci insegna che, in generale, la presenza di gradienti di concentrazione alla fine sarà dissipata dai processi di trasporto di massa, che portano costantemente i sistemi a uno stato di equilibrio. Tuttavia, anche se la seconda legge della termodinamica ci dice la natura dello stato finale di un sistema (ad esempio, concentrazioni uniformi), non ci dice quanto tempo ci vorrà per raggiungere quello stato. Le membrane si sono evolute per formare una barriera molto efficace al trasferimento spontaneo di molte specie ioniche e molecolari. Per stimare la scala temporale per l’equalizzazione delle concentrazioni, abbiamo bisogno di conoscere i tassi di trasporto di massa, che dipendono da proprietà chiave del materiale come le costanti di diffusione e le permeabilità.
Una classe di “leggi” di grande successo, che descrive il comportamento dei sistemi che hanno subito qualche piccolo allontanamento dall’equilibrio, sono le leggi del trasporto lineare. Queste leggi postulano una semplice relazione lineare tra la velocità di trasporto di qualche quantità di interesse e la forza motrice associata. Per il trasporto di massa, c’è una relazione lineare tra il flusso (cioè il numero di molecole che attraversano un’area per unità di tempo) e la differenza di concentrazione (che serve come forza motrice pertinente). Per il trasporto attraverso le membrane, queste idee sono state codificate nella semplice equazione (per il soluto neutro) j= – p-(cin-cout), dove j è il flusso netto nella cellula, cin e cout si riferiscono alle concentrazioni all’interno e all’esterno della regione legata alla membrana, e p è un parametro materiale noto come permeabilità. Le unità di p possono essere dedotte notando che il flusso ha unità di numero/(area x tempo) e la concentrazione ha unità di numero/volume, il che implica che le unità di p stesso sono lunghezza/tempo. Come molte grandezze di trasporto (per esempio le conducibilità elettriche dei materiali che vanno oltre 30 ordini di grandezza), la permeabilità ha una gamma dinamica molto ampia come illustrato nella figura 1. Come si vede nella figura, i bilayer lipidici hanno una gamma di permeabilità di quasi 1010 volte.
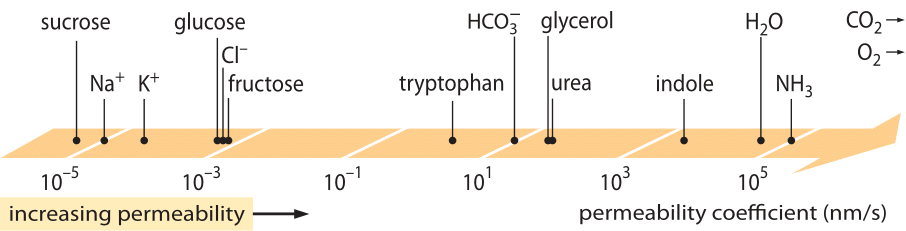
Figura 1: La vasta gamma di permeabilità di membrana di diversi composti nella cellula. Le membrane sono più permeabili ai composti non carichi e meno permeabili agli ioni carichi. Si noti che l’esistenza di canali ionici renderà la permeabilità apparente quando sono aperti diversi ordini di grandezza più alta. Le unità sono scelte come nm/s e diversi nm è la larghezza caratteristica della membrana. Figura adattata da R. N. Robertson, The Lively Membranes, Cambridge University Press, 1983. Il valore per il glucosio è più piccolo che in Robertson basato su diverse fonti come BNID 110830, 110807. Altre fonti di dati: BNID 110729, 110731, 110816, 110824, 110806.
Quali parametri fisico-chimici guidano la posizione di un composto su questa scala di permeabilità? Una regola empirica è che le molecole piccole hanno una permeabilità più alta delle molecole più grandi. Un’altra regola generale è che i composti neutri possono attraversare la membrana molti ordini di grandezza più velocemente dei composti carichi simili. Tra i composti carichi, i composti negativi (anionici) tendono ad avere permeabilità molto più alte dei composti positivi (cationici). La cosiddetta regola di Overton afferma che la permeabilità della membrana aumenta con l’idrofobicità, dove l’idrofobicità è la tendenza di un composto a preferire un solvente non polare a un solvente polare (acquoso). La regola di Overton prevede che le molecole cariche (non idrofobiche), come gli ioni, tenderanno ad avere una bassa permeabilità in quanto incorrono in una penalità energetica associata alla penetrazione della membrana, mentre i gas dissolti come O2 e CO2, che sono idrofobici (in quanto non caricati e simmetrici), avranno un’alta permeabilità. Infatti, la permeabilità delle membrane lipidiche a bilayer alla CO2 danno valori che sono 0,01-1 cm/s (sì, le misure di permeabilità hanno incertezze molto alte tra diversi laboratori, BNID 110004, 110617, 102624), superiori a tutti gli altri valori mostrati nella Figura 1. Questo valore mostra che la barriera creata dalla membrana cellulare è in realtà meno di un ostacolo rispetto alla barriera causata dallo strato non agitato di acqua che inghiotte la membrana cellulare dall’esterno. Tale deduzione può essere derivata dall’equazione per il coefficiente di permeabilità di un ostacolo, dato da p=K x D/l dove l è la larghezza, D il coefficiente di diffusione e K il coefficiente di partizione tra i media e il materiale dell’ostacolo. Questo è anche conosciuto come il modello “solubilità-diffusione” per la permeabilità dove questi denotano gli effetti K e D che sono due passi che influenzano la permeabilità. Per uno strato non agitato di acqua K=1 in quanto è molto simile ai media, ma per la membrana il valore per tutti i materiali, tranne i più idrofobici, è di solito diversi ordini di grandezza inferiore a 1. Questa dipendenza da K è il cuore della regola di Overton menzionata sopra. L’alta permeabilità per la CO2 suggerisce anche che i canali come le acquaporine che sono stati suggeriti per servire per il trasporto di gas nella cellula non sono necessari perché la membrana è abbastanza permeabile. Per vedere come le proprietà della membrana influenzano la composizione chimica dei metaboliti, passiamo a calcolare il tempo di perdita per diversi composti
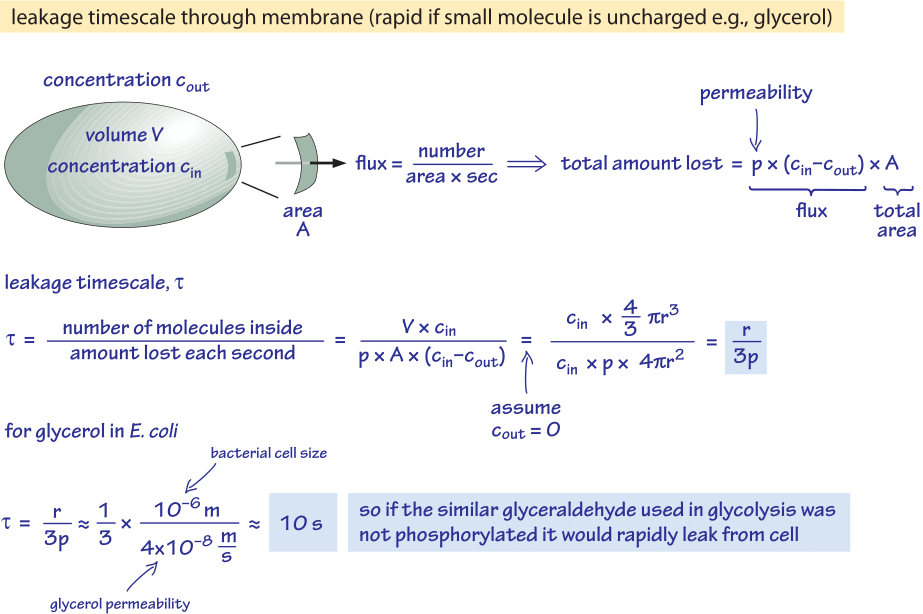
Figura 2: Calcolo a ritroso del tempo di diffusione passiva di una molecola di glucosio non fosforilato fuori da una cellula batterica. Le implicazioni funzionali sono poi considerate per le cellule in rapida crescita dove l’effetto è trascurabile e per le cellule in stato stazionario dove può causare una perdita apprezzabile di risorse.
Consideriamo il glicerolo, per esempio. L’analisi mostrata nella figura 2 fornisce una stima del tempo della sua fuoriuscita dalla cellula se la molecola non viene fosforilata o altrimenti convertita in una forma più idrofila. La permeabilità della membrana cellulare al glicerolo è p≈10-100 nm/s (BNID 110824) come si può leggere dalla Figura 1. La scala temporale per una molecola di glicerolo all’interno della cellula per sfuggire di nuovo al mezzo circostante, assumendo nessun flusso di ritorno nella cellula (cout=0), può essere grossolanamente stimata notando che l’efflusso dalla cellula è p-A-cin dove A è l’area della superficie cellulare. La scala temporale si trova prendendo la quantità totale nella cellula, V-cin (dove V è il volume della cellula o più precisamente il volume dell’acqua della cellula), e dividendo per questo flusso che risulta per una cellula batterica (r≈1 μm) in una scala temporale:
t =V-cin/p-A-cin =(4πr3/3)/(4πr2-3×10-6 cm/s) ≈ 10 s.
Questa è una stima grezza perché non abbiamo tenuto conto della concentrazione decrescente di cin con il tempo che darà un fattore di correzione di 1/ln(2), cioè meno di 2 volte di aumento. Quello che impariamo da queste stime è che se gli intermedi glicolitici gliceraldeide o diidrossiacetone che sono molto simili al glicerolo non fossero fosforilati, con conseguente aggiunta di una carica, sarebbero persi nel mezzo per diffusione attraverso la membrana cellulare. Nei mezzi di laboratorio, dove una fonte di carbonio è fornita in abbondanza, questo non è un grosso problema, ma in un ambiente naturale dove le cellule sono spesso in attesa in fase stazionaria per un impulso fortunato di nutrienti (E. coli si crede che passi mesi senza crescita dopo la sua espulsione dal corpo prima che trovi un nuovo ospite), la cellula può frenare le sue perdite assicurandosi che gli intermedi metabolici siano etichettati con una carica che impedirà loro di riattraversare la barriera presentata dal bilayer lipidico.




