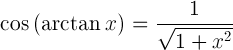Tabella dell’arctangente
| y | x = arctan(y) | |
|---|---|---|
| gradi | radiani | |
| -1.732050808 | -60° | -π/3 |
| -1 | -45° | -π/4 |
| -0.577350269 | -30° | -π/6 |
| 0 | 0° | 0 |
| 0.577350269 | 30° | π/6 |
| 1 | 45° | π/4 |
| 1.732050808 | 60° | π/3 |
Qual è la rettangente di 0?
arctan 0 = ?
La rettangente è la funzione tangente inversa.
Siccome, tan 0 = tan 0º = 0
L’ottangente di 0 è uguale alla funzione tangente inversa di 0, che è uguale a 0 radianti o 0 gradi:
arctan 0 = tan-1 0 = 0 rad = 0º
Qual è l’ottangente di 1 ?
arctan 1 = ?
L’arctangente è la funzione tangente inversa.
Siccome, tan π/4 = tan 45º = 1
L’ottangente di 1 è uguale alla funzione tangente inversa di 1, che è uguale a π/4 radianti o 45 gradi:
arctan 1 = tan-1 1 = π/4 rad = 45º
Qual è l’ottangente di 2 ?
arctan 2 = ?
L’arctangente è la funzione tangente inversa.
Siccome, tan 1,107 = tan 63,435º = 2
L’arctangente di 2 è uguale alla funzione tangente inversa di 2, che è uguale a 1.107 radianti o 63,435 gradi:
arctan 2 = tan-1 2 = 1,107 rad = 63,435º
Arctano dell’infinito
Qual è l’arctangente di infinito e meno infinito?
Arctano(∞) = ?
L’ottangente è la funzione tangente inversa.
Il limite dell’ottangente di x quando x si avvicina all’infinito è uguale a pi/2 radianti o 90 gradi:
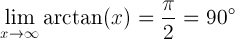
Il limite dell’ottangente di x quando x si avvicina a meno infinito è uguale a -pi/2 radianti o -90 gradi: 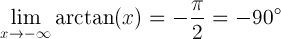
Derivata di arctan
Qual è la derivata della funzione ottangente di x?
La derivata della funzione arctangente di x è uguale a 1 diviso (1+x2)
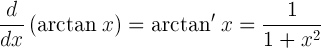
Integrale di arctan
Qual è l’integrale della funzione arctangente di x?
L’integrale indefinito della funzione arctangente di x è:

Grafico di arctan
Grafico di arctangente di x:
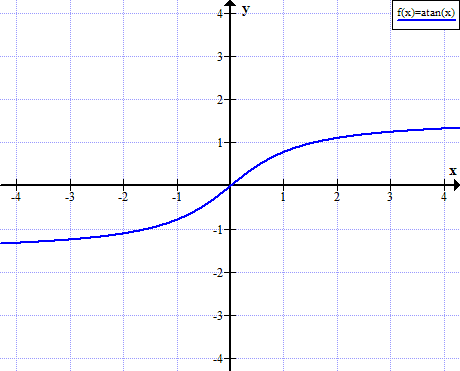
Qual è il seno di arctan(x)
sin( arctan(x) ) = ?
Il seno dell’arctangente di x è:
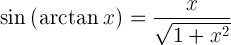
Qual è il coseno di arctan(x)
cos( arctan(x) ) = ?
Il coseno dell’arctangente di x è: