Descriveremo tre esempi dalle scienze della vita: uno dalla fisica, uno relativo alla genetica e uno da un esperimento sui topi. Sono molto diversi, eppure finiamo per usare la stessa tecnica statistica: l’adattamento di modelli lineari. I modelli lineari sono tipicamente insegnati e descritti nel linguaggio dell’algebra matriciale.
Esempi motivanti
Oggetti in caduta
Immaginate di essere Galileo nel XVI secolo che cerca di descrivere la velocità di un oggetto in caduta. Un assistente sale sulla Torre di Pisa e lascia cadere una palla, mentre diversi altri assistenti registrano la posizione in momenti diversi. Simuliamo alcuni dati usando le equazioni che conosciamo oggi e aggiungendo qualche errore di misura:
set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##metersGli assistenti consegnano i dati a Galileo e questo è ciò che vede:
mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")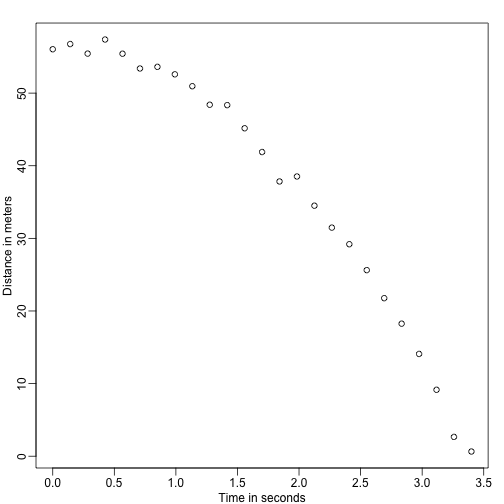
Non conosce l’equazione esatta, ma guardando il grafico qui sopra deduce che la posizione dovrebbe seguire una parabola. Quindi modella i dati con:
Con che rappresenta la posizione, che rappresenta il tempo e che tiene conto dell’errore di misurazione. Questo è un modello lineare perché è una combinazione lineare di quantità note (th s) chiamate predittori o covariate e parametri sconosciuti (the s).
Padre &altezze figlio
Ora immaginate di essere Francis Galton nel XIX secolo e di raccogliere dati di altezza appaiati da padri e figli. Sospettate che l’altezza sia ereditaria. I vostri dati:
library(UsingR)x=father.son$fheighty=father.son$sheightsembrano così:
plot(x,y,xlab="Father's height",ylab="Son's height")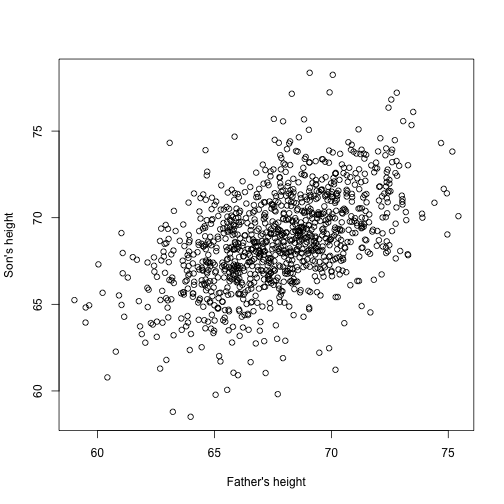
Le altezze dei figli sembrano aumentare linearmente con quelle dei padri. In questo caso, un modello che descrive i dati è il seguente:
Anche questo è un modello lineare con e , le altezze di padre e figlio rispettivamente, per la -esima coppia e un termine per tenere conto della variabilità extra. Qui pensiamo che l’altezza dei padri sia il fattore predittivo e che sia fisso (non casuale), quindi usiamo le minuscole. L’errore di misurazione da solo non può spiegare tutta la variabilità vista in . Questo ha senso perché ci sono altre variabili non presenti nel modello, per esempio l’altezza delle madri, la casualità genetica e i fattori ambientali.
Campioni casuali da popolazioni multiple
Qui leggiamo i dati sul peso corporeo dei topi che sono stati alimentati con due diete diverse: ad alto contenuto di grassi e di controllo (chow). Abbiamo un campione casuale di 12 topi per ciascuno. Siamo interessati a determinare se la dieta ha un effetto sul peso. Ecco i dati:
dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")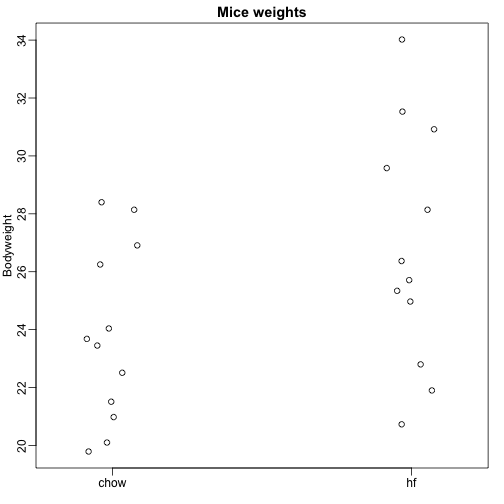
Vogliamo stimare la differenza di peso medio tra le popolazioni. Abbiamo dimostrato come farlo usando i test t e gli intervalli di confidenza, basati sulla differenza nelle medie dei campioni. Possiamo ottenere gli stessi esatti risultati usando un modello lineare:
con il peso medio della dieta chow, la differenza tra le medie, quando il topo riceve la dieta high fat (hf), quando riceve la dieta chow, e spiega le differenze tra i topi della stessa popolazione.
Modelli lineari in generale
Abbiamo visto tre esempi molto diversi in cui si possono usare modelli lineari. Un modello generale che comprende tutti gli esempi di cui sopra è il seguente:
Nota che abbiamo un numero generale di predittori. L’algebra matriciale fornisce un linguaggio compatto e un quadro matematico per calcolare e fare derivazioni con qualsiasi modello lineare che rientri nel quadro di cui sopra.
Stimare i parametri
Perché i modelli di cui sopra siano utili dobbiamo stimare l’incognita s. Nel primo esempio, vogliamo descrivere un processo fisico per il quale non possiamo avere parametri sconosciuti. Nel secondo esempio, comprendiamo meglio l’ereditarietà stimando quanto, in media, l’altezza del padre influenzi l’altezza del figlio. Nell’ultimo esempio, vogliamo determinare se c’è effettivamente una differenza: se .
L’approccio standard nella scienza è quello di trovare i valori che minimizzano la distanza del modello montato dai dati. La seguente è chiamata equazione dei minimi quadrati (LS) e la vedremo spesso in questo capitolo:
Una volta trovato il minimo, chiameremo i valori le stime dei minimi quadrati (LSE) e li denoteremo con . La quantità ottenuta valutando l’equazione dei minimi quadrati alle stime è chiamata somma residua dei quadrati (RSS). Poiché tutte queste quantità dipendono da , sono variabili casuali. Le s sono variabili casuali e alla fine eseguiremo l’inferenza su di esse.
Esempio di oggetto in caduta rivisitato
Grazie al mio insegnante di fisica del liceo, so che l’equazione della traiettoria di un oggetto in caduta è:
con e l’altezza e la velocità di partenza rispettivamente. I dati che abbiamo simulato sopra hanno seguito questa equazione e aggiunto l’errore di misurazione per simulare nle osservazioni per la caduta della palla dalla torre di Pisa. Ecco perché abbiamo usato questo codice per simulare i dati:
g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)Ecco come appaiono i dati con la linea continua che rappresenta la vera traiettoria:
plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)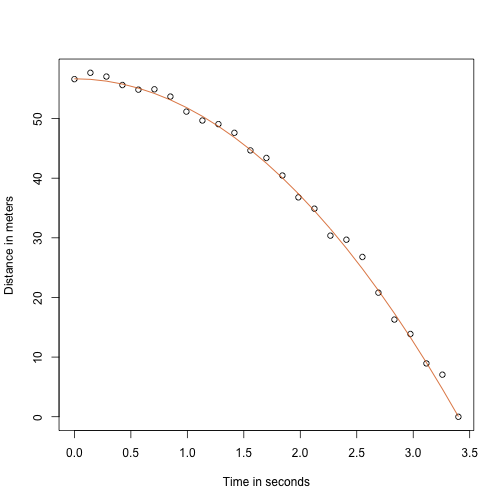
Ma stavamo facendo finta di essere Galileo e quindi non sappiamo i parametri del modello. I dati suggeriscono che è una parabola, quindi la modelliamo come tale:
Come troviamo la LSE?
La funzione lm
In R possiamo adattare questo modello semplicemente usando la funzione lm. Descriveremo questa funzione in dettaglio più tardi, ma ecco un’anteprima:
tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17Ci dà il LSE, così come gli errori standard e i valori p.
Parte di ciò che facciamo in questa sezione è spiegare la matematica dietro questa funzione.
La stima dei minimi quadrati (LSE)
Scriviamo una funzione che calcola l’RSS per qualsiasi vettore :
rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}Quindi per qualsiasi vettore tridimensionale otteniamo un RSS. Ecco un grafico dell’RSS in funzione di quando manteniamo fissi gli altri due:
Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)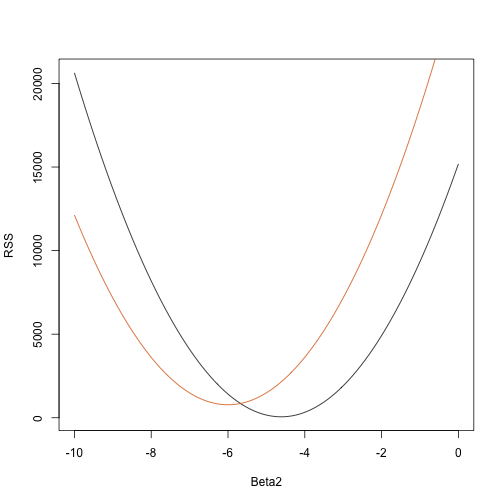
I tentativi ed errori qui non funzionano. Invece, possiamo usare il calcolo: prendere le derivate parziali, metterle a 0 e risolvere. Naturalmente, se abbiamo molti parametri, queste equazioni possono diventare piuttosto complesse. L’algebra lineare fornisce un modo compatto e generale di risolvere questo problema.
Più su Galton (Avanzato)
Studiando i dati padre-figlio, Galton fece un’affascinante scoperta usando l’analisi esplorativa.
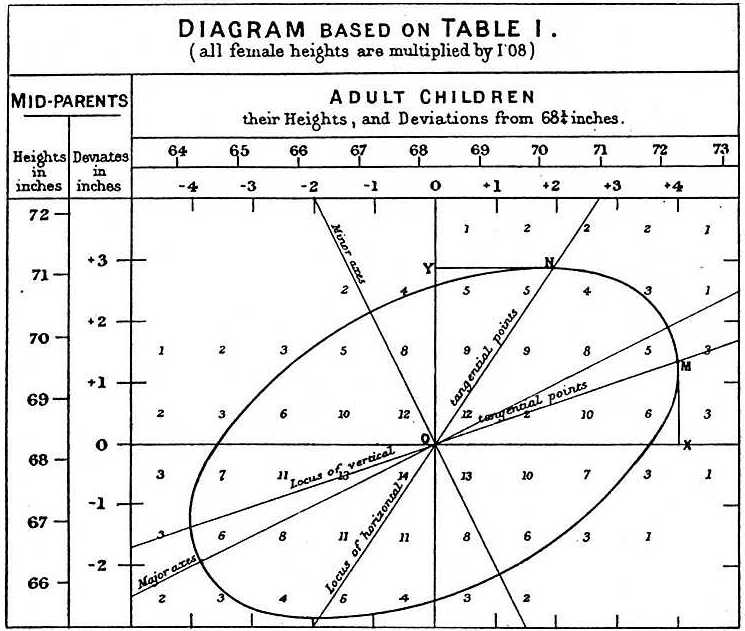
Ha notato che se tabulava il numero di coppie di altezza padre-figlio e seguiva tutti i valori x,y con gli stessi totali nella tabella, essi formavano un’ellissi. Nel grafico qui sopra, fatto da Galton, si vede l’ellissi formata dalle coppie che hanno 3 casi. Questo ha poi portato a modellare questi dati come normali bivariate correlate che abbiamo descritto prima:
Abbiamo descritto come possiamo usare la matematica per mostrare che se si mantiene fissa (condizione di essere ) la distribuzione di è normalmente distribuita con media: e deviazione standard . Si noti che è la correlazione tra e , il che implica che se fissiamo , segue di fatto un modello lineare. I parametri e nel nostro semplice modello lineare possono essere espressi in termini di , e .
.