Possiamo usare Gibbs-Helmholtz per ottenere la dipendenza dalla temperatura di \(K\)
}{∂T} \destra)_P = \dfrac{-Δ_rH^o}{T^2}]
All’equilibrio, possiamo equiparare \(Δ_rG^o\) a \(-RT\ln K\) così otteniamo:
\}{∂T} \destra)_P = \dfrac{Δ_rH^o}{RT^2}
Vediamo che se \(K\) aumenta o diminuisce con la temperatura è legato al fatto che l’entalpia di reazione sia positiva o negativa. Se la temperatura è cambiata abbastanza poco che \(Δ_rH^o\) può essere considerato costante, possiamo tradurre un valore di \(K\) ad una temperatura in un altro integrando l’espressione precedente, otteniamo una derivazione simile a quella della depressione del punto di fusione:
\
Se è richiesta più precisione potremmo correggere le variazioni di temperatura di ΔrHo usando i dati della capacità termica.
Come \(K\) aumenta o diminuisce con la temperatura è legato al fatto che l’entalpia di reazione sia positiva o negativa.
L’espressione per \(K\) è una funzione piuttosto sensibile della temperatura data la sua dipendenza esponenziale dalla differenza dei coefficienti stechiometrici Un modo per vedere la sensibile dipendenza dalla temperatura delle costanti di equilibrio è di ricordare che
Tuttavia, dato che a pressione e temperatura costanti
‖
L’equazione ‗(‗ref{18}} diventa
‗
Prendendo il log naturale di entrambi i lati, si ottiene una relazione lineare tra ‗(‗ln K ‖) e le entalpie ed entropie standard:
che è conosciuta come l’equazione di van’t Hoff. Mostra che un grafico di \(\ln K\) contro \(1/T\) dovrebbe essere una linea con pendenza \(-\Delta_r{H^o}/R\) e intercetta \(\Delta_r{S^o}/R\).
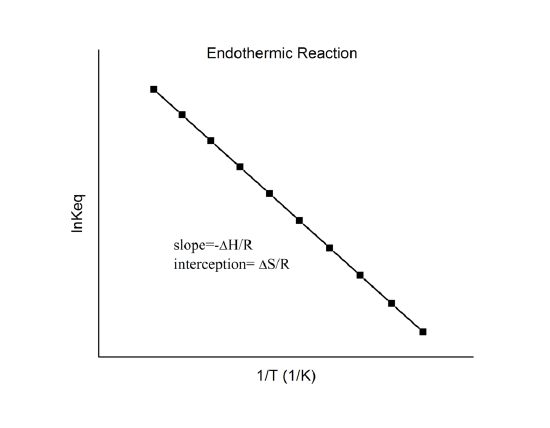
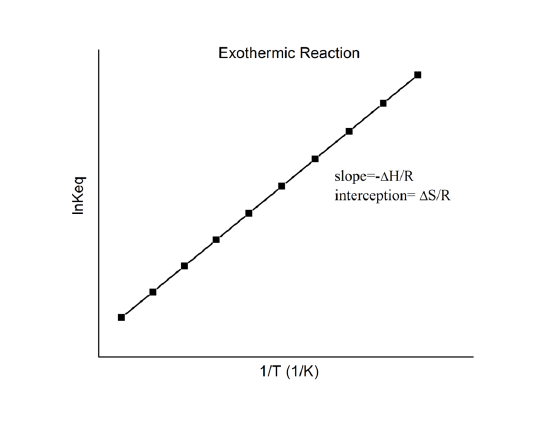
Quindi, queste quantità possono essere determinate dai dati \(\ln K\) vs. \(1/T\) senza fare calorimetria. Naturalmente, il presupposto principale qui è che \(\Delta_r{H^o}}) e \(\Delta_r{S^o}) siano solo debolmente dipendenti da \(T\), che di solito è valido.