Understanding LSTM Networks

Recurrent Neural Networks

Az emberek nem kezdik minden másodpercben elölről a gondolkodásukat. Ahogy ezt az esszét olvasod, minden egyes szót az előző szavak megértése alapján értesz meg. Nem dobsz el mindent, és nem kezded elölről a gondolkodást. A gondolatai állandósággal rendelkeznek.

A hagyományos neurális hálózatok erre nem képesek, és ez nagy hiányosságnak tűnik. Képzeljük el például, hogy egy film minden egyes pontján azt akarjuk osztályozni, hogy milyen esemény történik. Nem világos, hogy egy hagyományos neurális hálózat hogyan tudná a film korábbi eseményeire vonatkozó következtetéseit felhasználni a későbbi eseményekhez.

A rekurrens neurális hálózatok megoldják ezt a problémát. Ezek olyan hálózatok, amelyekben hurkokat tartalmaznak, lehetővé téve az információ fennmaradását.

A fenti ábrán a neurális hálózat egy darabja, \(A\), megvizsgál egy \(x_t\) bemenetet, és kiad egy \(h_t\) értéket. Egy hurok lehetővé teszi az információ átadását a hálózat egyik lépéséből a következőbe.

Ezek a hurkok teszik a rekurrens neurális hálózatokat kissé titokzatossá. Ha azonban egy kicsit jobban belegondolunk, kiderül, hogy nem sokban különböznek a normál neurális hálózatoktól. A rekurrens neurális hálózatot úgy lehet elképzelni, mint ugyanazon hálózat több példányát, amelyek mindegyike üzenetet továbbít egy utódnak. Nézzük meg, mi történik, ha feltekerjük a hurkot:

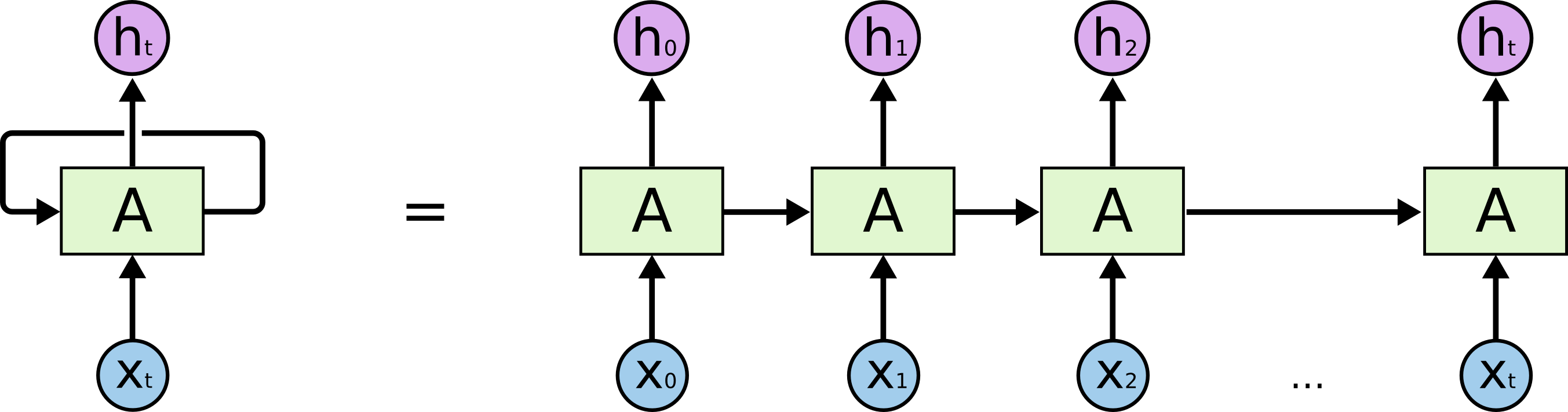
Ez a láncszerűség megmutatja, hogy a rekurrens neurális hálózatok szoros kapcsolatban állnak a sorozatokkal és a listákkal. Ezek a neurális hálózatok természetes architektúrája az ilyen adatokhoz.

És bizony használják is őket! Az elmúlt néhány évben hihetetlen sikereket értek el az RNN-ek alkalmazásával a legkülönbözőbb problémákra: beszédfelismerés, nyelvi modellezés, fordítás, képfeliratozás… A lista folytatható. Az RNN-ekkel elérhető elképesztő eredmények megvitatását Andrej Karpathy kiváló blogbejegyzésére hagyom: The Unreasonable Effectiveness of Recurrent Neural Networks. De tényleg eléggé elképesztőek.

Ezeknek a sikereknek a lényege az “LSTM-ek” használata, a rekurrens neurális hálózatok egy nagyon speciális fajtája, amely sok feladatban sokkal, de sokkal jobban működik, mint a hagyományos változat. Szinte minden izgalmas, rekurrens neurális hálózaton alapuló eredményt velük értek el. Ez a dolgozat ezeket az LSTM-eket fogja megvizsgálni.

A hosszú távú függőségek problémája

Az RNN-ek egyik vonzereje az az elképzelés, hogy képesek lehetnek összekapcsolni a korábbi információkat a jelenlegi feladattal, például a korábbi videóképek felhasználásával a jelenlegi képkocka megértését. Ha az RNN-ek képesek lennének erre, rendkívül hasznosak lennének. De vajon képesek-e? Ez attól függ.

Néha csak a közelmúltbeli információkra van szükségünk a jelenlegi feladat elvégzéséhez. Vegyünk például egy nyelvi modellt, amely a következő szót próbálja megjósolni az előzőek alapján. Ha a “felhők az égen” utolsó szavát próbáljuk megjósolni, nincs szükségünk további kontextusra – elég nyilvánvaló, hogy a következő szó az ég lesz. Ilyen esetekben, amikor a releváns információ és a szükséges hely között kicsi a különbség, az RNN-ek megtanulhatják használni a múltbeli információt.

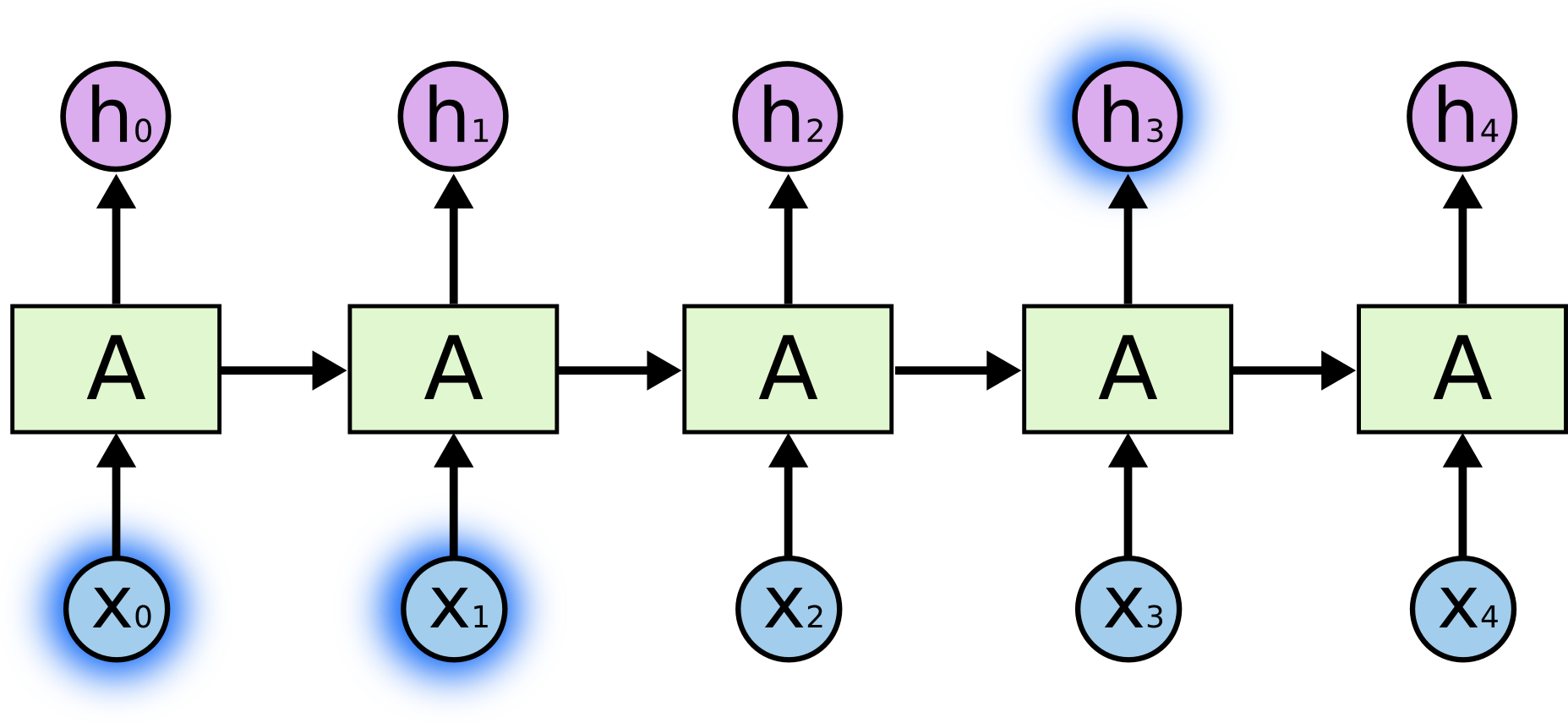
De vannak olyan esetek is, amikor több kontextusra van szükségünk. Gondoljunk arra, hogy megpróbáljuk megjósolni az utolsó szót a “Franciaországban nőttem fel… Folyékonyan beszélek franciául” szövegben. A legújabb információk szerint a következő szó valószínűleg egy nyelv neve, de ha le akarjuk szűkíteni, hogy melyik nyelvről van szó, akkor szükségünk van a franciaországi kontextusra, még régebbről. Teljesen lehetséges, hogy a releváns információ és az a pont, ahol szükség van rá, közötti rés nagyon nagyra nő.

Sajnos, ahogy ez a rés nő, az RNN-ek képtelenné válnak arra, hogy megtanulják összekapcsolni az információt.

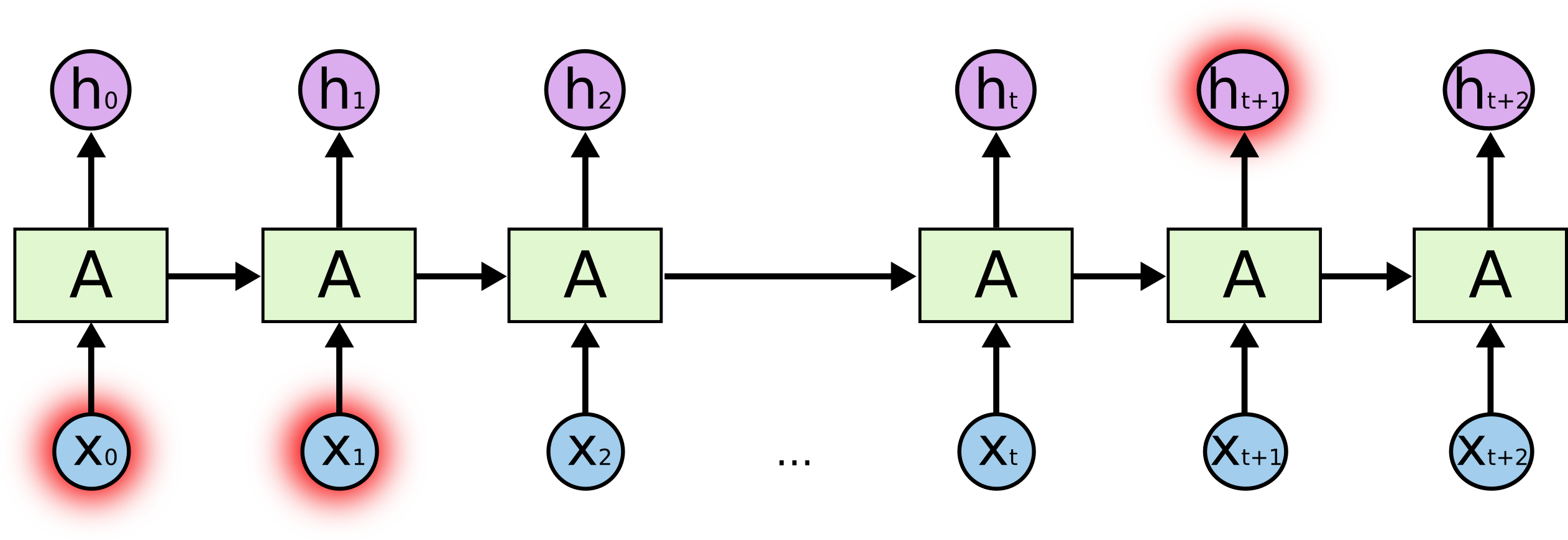
Elméletben az RNN-ek abszolút képesek az ilyen “hosszú távú függőségek” kezelésére. Egy ember gondosan kiválaszthatná számukra a paramétereket, hogy ilyen formájú játékproblémákat oldjanak meg. Sajnos a gyakorlatban úgy tűnik, hogy az RNN-ek nem képesek megtanulni ezeket. A problémát Hochreiter (1991) és Bengio, et al. (1994) vizsgálta alaposan, és találtak néhány elég alapvető okot, amiért ez nehéz lehet.

Az LSTM-eknek szerencsére nincs ilyen problémájuk!

LSTM hálózatok

A hosszú rövid távú memóriájú hálózatok – általában csak “LSTM-nek” nevezik őket – az RNN-ek egy speciális fajtája, amely képes hosszú távú függőségek tanulására. Hochreiter & Schmidhuber (1997) vezette be őket, majd az ezt követő munkákban sokan finomították és népszerűsítették.1 Rendkívül jól működnek a problémák széles skáláján, és ma már széles körben használják őket.

Az LSTM-eket kifejezetten úgy tervezték, hogy elkerüljék a hosszú távú függőségi problémát. Az információ hosszú időn keresztül történő megjegyzése gyakorlatilag az alapértelmezett viselkedésük, nem pedig olyasmi, amit nehezen tanulnak meg!

Minden rekurrens neurális hálózat az ismétlődő neurális hálózati modulok láncolatának formája. A standard RNN-ekben ez az ismétlődő modul nagyon egyszerű felépítésű lesz, például egyetlen tanh réteggel.

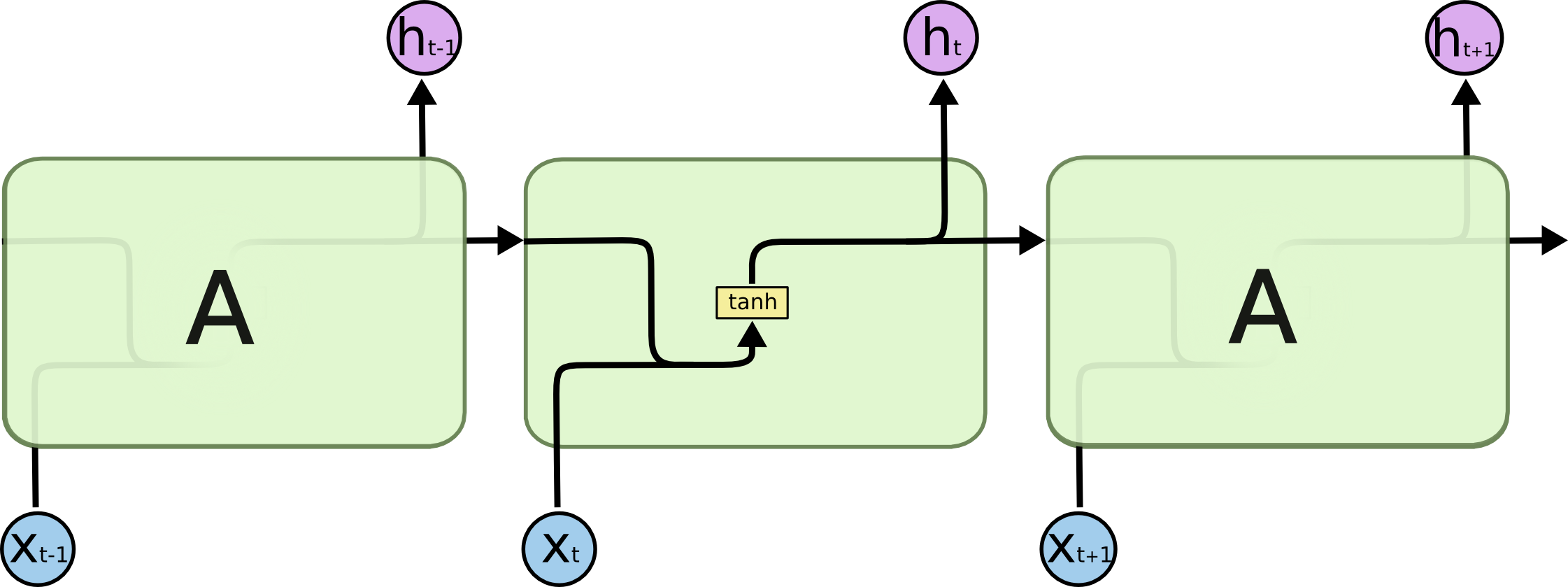
A LSTM-ek is ilyen láncszerű felépítésűek, de az ismétlődő modul más szerkezetű. Ahelyett, hogy egyetlen neurális hálózati réteg lenne, négy van, amelyek különleges módon kölcsönhatásba lépnek egymással.

Ne törődjünk a részletekkel. Később lépésről lépésre végigmegyünk az LSTM-diagramon. Egyelőre csak próbáljunk megbarátkozni az általunk használt jelöléssel.

A fenti diagramon minden egyes vonal egy teljes vektort hordoz, az egyik csomópont kimenetétől a többi bemenetéig. A rózsaszín körök a pontszerű műveleteket, például a vektorok összeadását jelképezik, míg a sárga dobozok a tanult neurális hálózat rétegeit. Az összefutó vonalak az összefűzést jelölik, míg az elágazó vonalak azt jelentik, hogy a vonal tartalma másolásra kerül, és a másolatok különböző helyekre kerülnek.

Az LSTM-ek alapötlete

Az LSTM-ek kulcsa a sejtállapot, az ábra tetején futó vízszintes vonal.

A sejtállapot olyan, mint egy futószalag. Egyenesen végigfut az egész láncon, csak néhány kisebb lineáris kölcsönhatással. Nagyon könnyű, hogy az információ csak úgy, változatlanul végigfolyjon rajta.

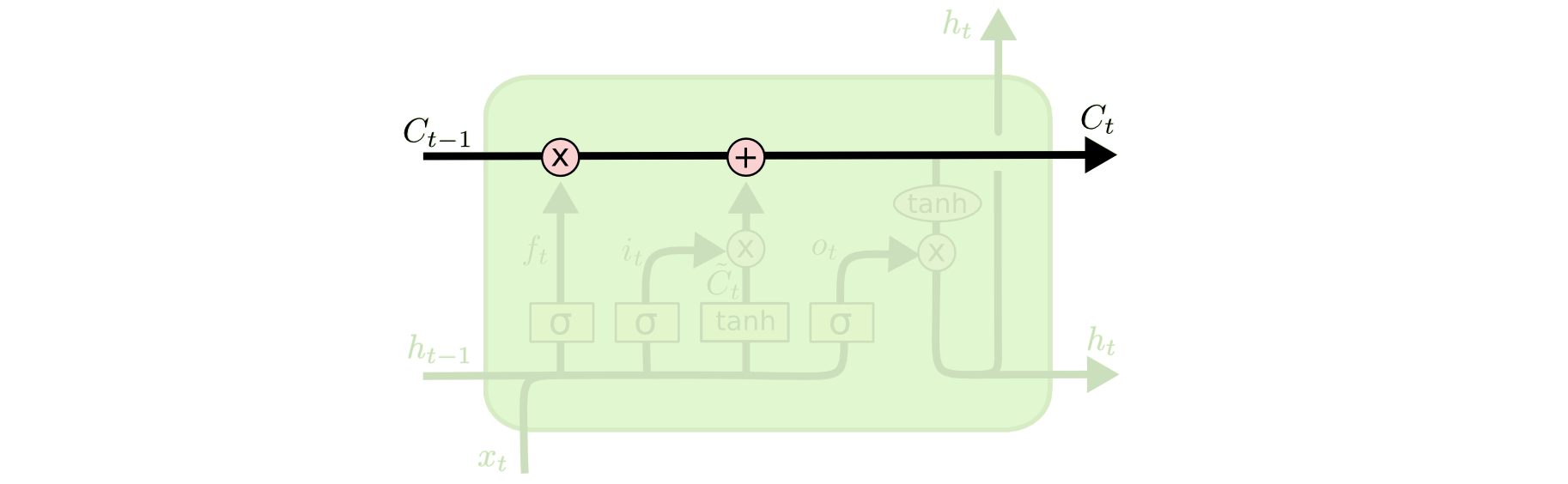
Az LSTM-nek megvan a képessége arra, hogy információt távolítson el vagy adjon hozzá a sejtállapothoz, amit gondosan szabályoznak a kapuknak nevezett struktúrák.

A kapuk egy módja annak, hogy opcionálisan átengedjük az információt. Ezek egy sigmoid neurális háló rétegből és egy pontszerű szorzási műveletből állnak.

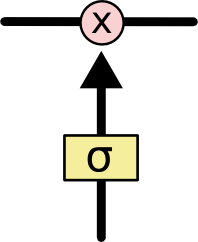
A sigmoid réteg nulla és egy közötti számokat ad ki, amelyek leírják, hogy az egyes összetevőkből mennyit kell átengedni. A nulla érték azt jelenti, hogy “ne engedjünk át semmit”, míg az egyes érték azt jelenti, hogy “engedjünk át mindent!”

Egy LSTM három ilyen kapuval rendelkezik, hogy védje és ellenőrizze a sejt állapotát.

Lépésről lépésre LSTM végigjárás

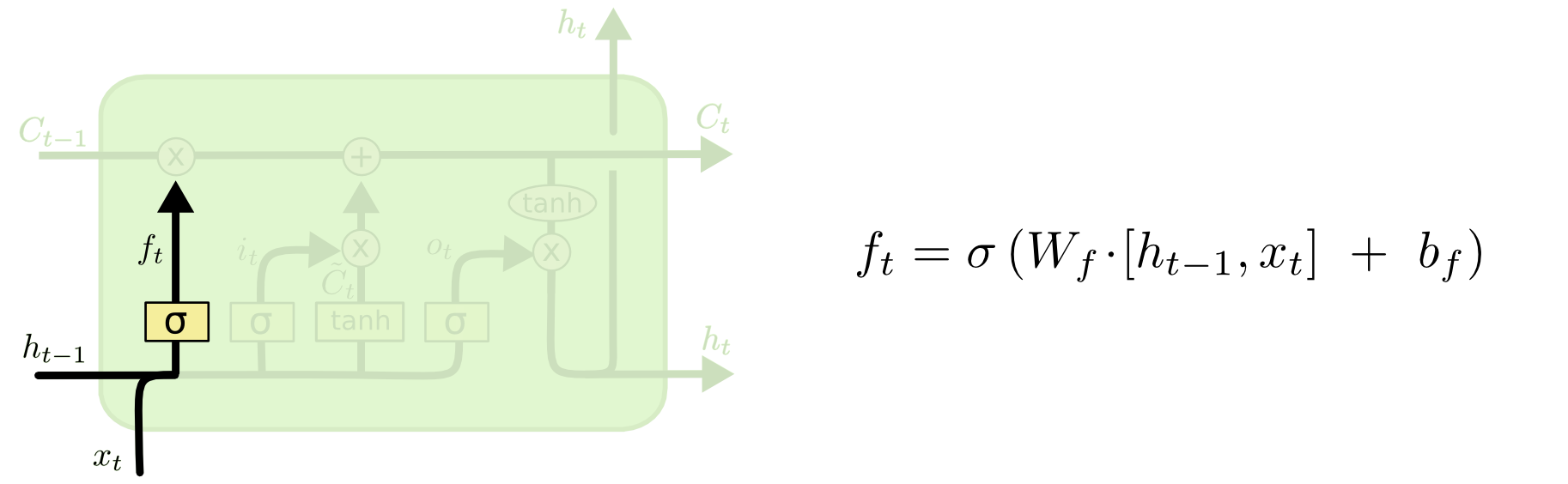
LSTM-ünk első lépése, hogy eldöntsük, milyen információt dobunk ki a sejt állapotából. Ezt a döntést egy szigmoid réteg, az úgynevezett “felejtsd el a kaput réteg” hozza meg. Megnézi az \(h_{t-1}\) és \(x_t\) értékeket, és az \(0\) és \(1\) közötti számot adja ki a cella \(C_{t-1}\) állapotának minden egyes számához. Az \(1\) azt jelenti, hogy “ezt teljesen tartsd meg”, míg az \(0\) azt jelenti, hogy “ettől teljesen szabadulj meg.”

Visszatérjünk vissza a példánkhoz, amikor egy nyelvi modell megpróbálja megjósolni a következő szót az összes előző alapján. Egy ilyen problémában a cella állapota tartalmazhatja az aktuális alany nemét, hogy a megfelelő névmásokat használhassuk. Amikor egy új alanyt látunk, szeretnénk elfelejteni a régi alany nemét.

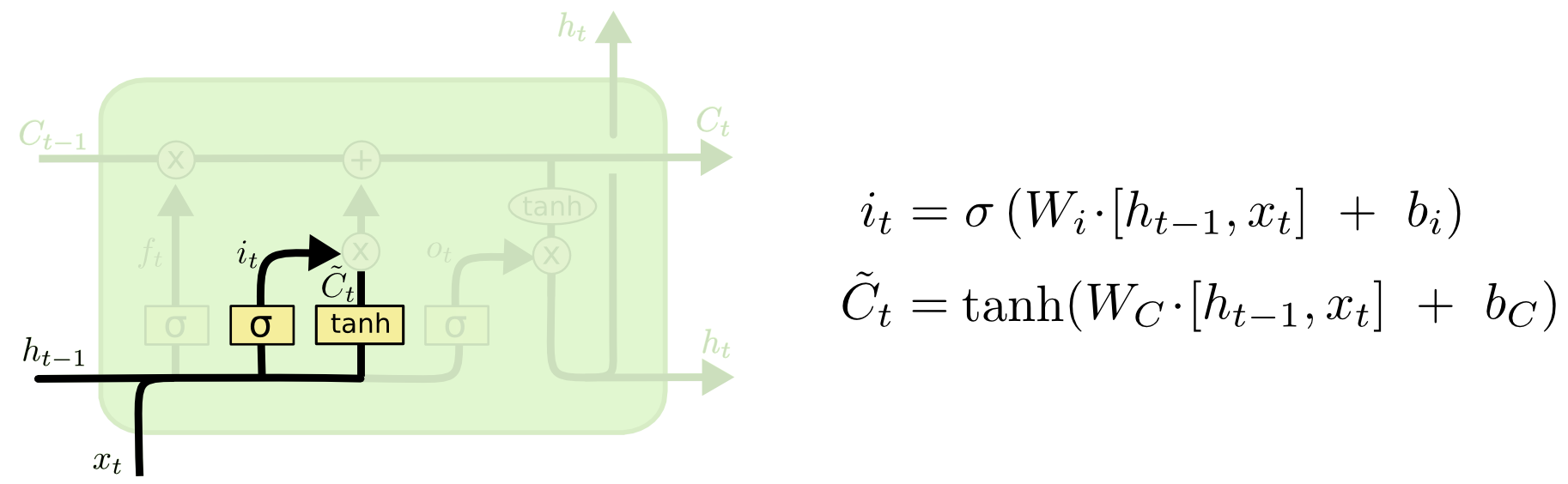
A következő lépés az, hogy eldöntjük, milyen új információt fogunk tárolni a sejtállapotban. Ennek két része van. Először egy “bemeneti kapurétegnek” nevezett szigmoid réteg dönt arról, hogy mely értékeket frissítjük. Ezután egy tanh réteg létrehoz egy vektort az új jelölt értékekből, \(\tilde{C}_t\), amelyeket hozzáadhatunk az állapothoz. A következő lépésben ezt a kettőt kombináljuk, hogy létrehozzuk az állapot frissítését.

A nyelvi modellünk példájában az új alany nemét szeretnénk hozzáadni a sejt állapotához, hogy a régi, elfelejtett nem helyébe lépjen.

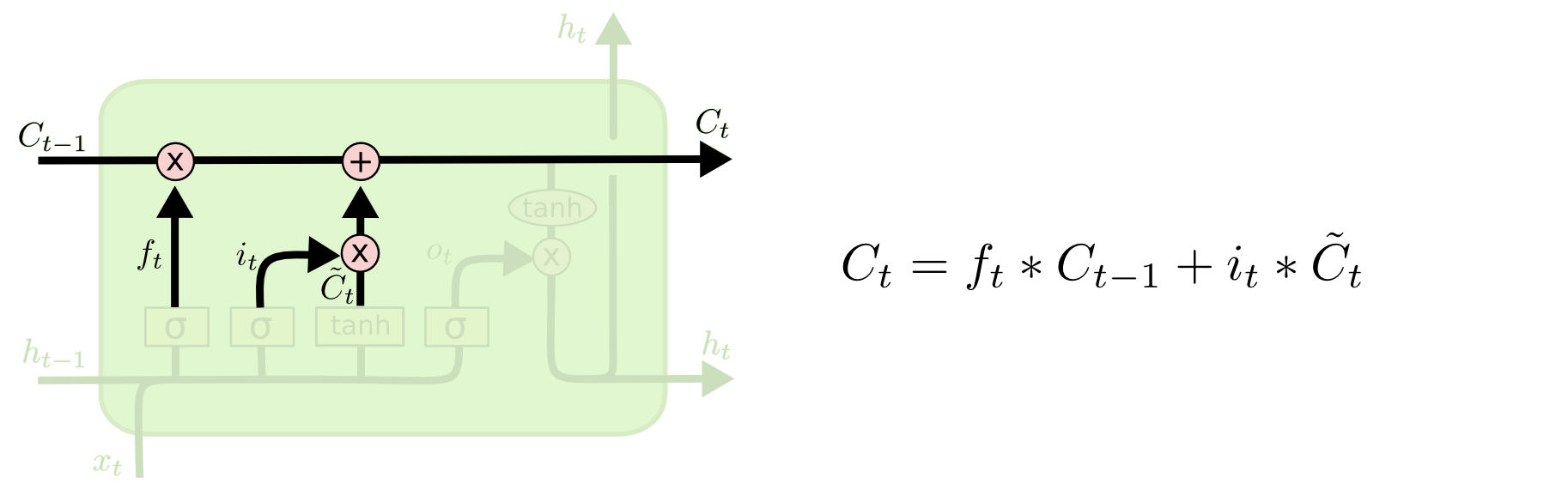
Most itt az ideje, hogy a régi sejt állapotot, \(C_{t-1}\), az új sejt állapotba \(C_t\) frissítsük. Az előző lépések már eldöntötték, hogy mit kell tennünk, már csak ténylegesen meg kell tennünk.

Megszorozzuk a régi állapotot \(f_t\) értékkel, elfelejtve azokat a dolgokat, amelyekről korábban úgy döntöttünk, hogy elfelejtjük. Ezután hozzáadjuk \(i_t*\tilde{C}_t\). Ez az új jelölt értékek, azzal skálázva, hogy mennyivel döntöttünk az egyes állapotértékek frissítéséről.

A nyelvi modell esetében ez az a pont, ahol tulajdonképpen elhagynánk a régi alany nemére vonatkozó információt, és hozzáadnánk az új információt, ahogy az előző lépésekben döntöttünk.

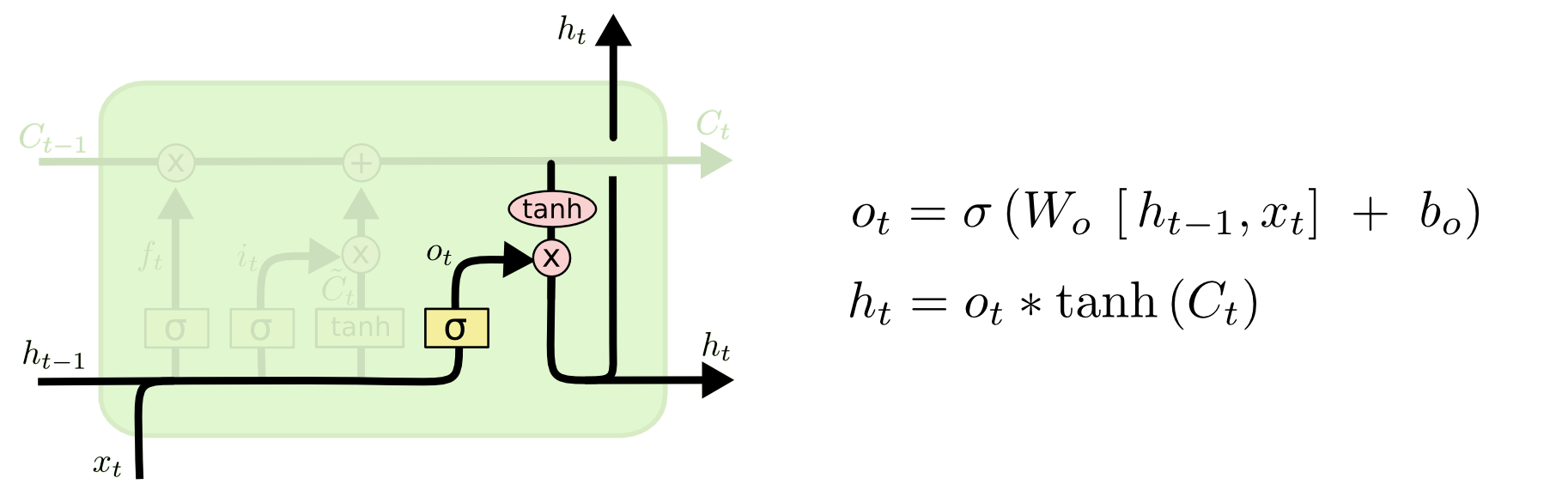
Végül el kell döntenünk, hogy mit fogunk kiadni. Ez a kimenet a cellánk állapotán fog alapulni, de egy szűrt változat lesz. Először lefuttatunk egy szigmoid réteget, amely eldönti, hogy a sejtállapot mely részeit fogjuk kiadni. Ezután a sejtállapotot \(\tanh\) keresztülvisszük (hogy az értékek \(-1\) és \(1\) közé kerüljenek), és megszorozzuk a szigmoid kapu kimenetével, így csak azokat a részeket adjuk ki, amelyekről döntöttünk.

A nyelvi modell példájában, mivel most látott egy alanyt, lehet, hogy egy igére vonatkozó információt akar kiadni, arra az esetre, ha az következik. Például kiadhatja, hogy az alany egyes vagy többes számban van-e, hogy tudjuk, milyen alakban kell az igét ragozni, ha ez következik.

Variációk a hosszú rövid távú memóriára

Az, amit eddig leírtam, egy eléggé átlagos LSTM. De nem minden LSTM azonos a fentiekkel. Valójában úgy tűnik, hogy szinte minden LSTM-ekkel foglalkozó cikk egy kissé eltérő változatot használ. A különbségek apróak, de érdemes megemlíteni néhányat közülük.

Az egyik népszerű LSTM-változat, amelyet Gers & Schmidhuber (2000) vezetett be, a “kukucskáló kapcsolatok” hozzáadása. Ez azt jelenti, hogy hagyjuk, hogy a kapurétegek belenézzenek a cella állapotába.

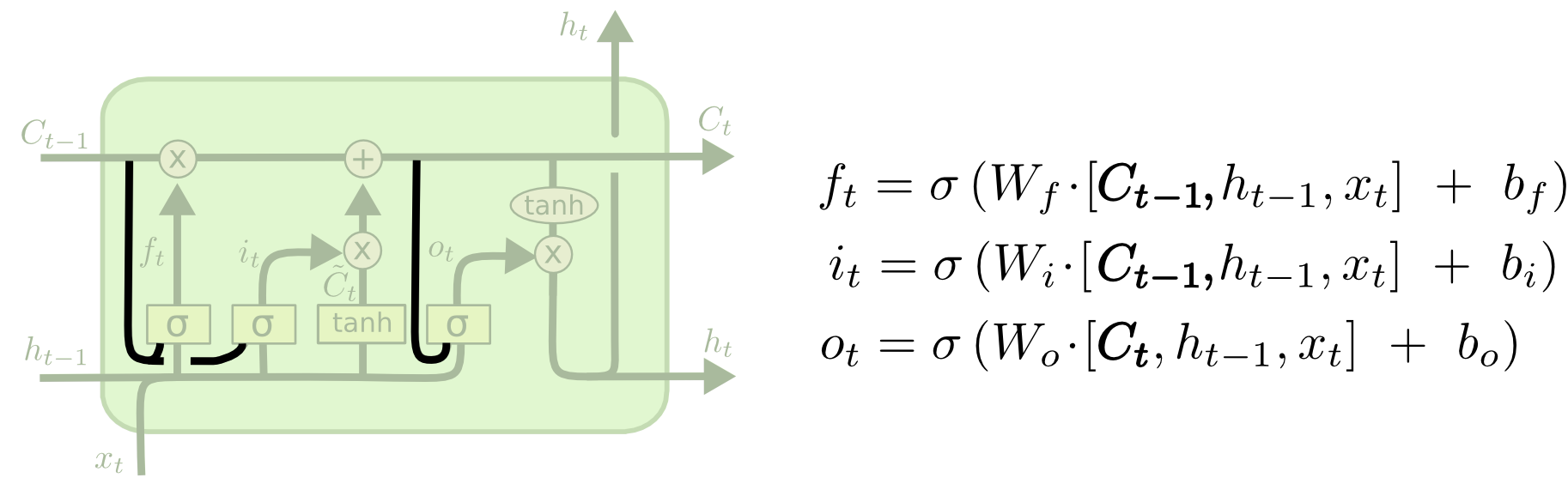
A fenti ábra minden kapuhoz kukucskálókat ad, de sok dolgozatban néhány kukucskálót megadnak, másokat nem.

Egy másik variáció a kapcsolt felejtés és bemeneti kapuk használata. Ahelyett, hogy külön-külön döntenénk arról, hogy mit felejtsünk el, és mihez adjunk új információt, ezeket a döntéseket együtt hozzuk meg. Csak akkor felejtünk, ha valamit be fogunk adni helyette. Csak akkor adunk be új értékeket az állapotba, amikor elfelejtünk valami régebbit.

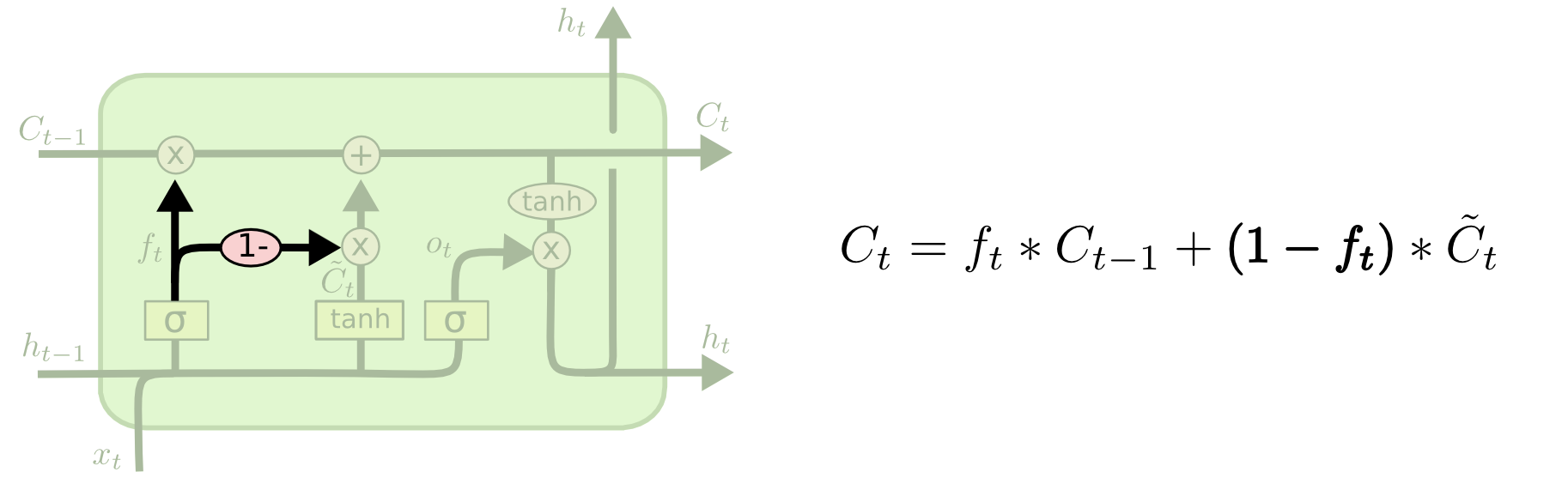
Az LSTM kissé drámaibb változata a Cho, et al. (2014) által bemutatott Gated Recurrent Unit, azaz GRU. Ez a felejtési és bemeneti kapukat egyetlen “frissítési kapuvá” egyesíti. Összevonja továbbá a cella állapotát és a rejtett állapotot, és néhány más változtatást is végrehajt. Az így kapott modell egyszerűbb, mint a standard LSTM modellek, és egyre népszerűbbé válik.

Ez csak néhány a legjelentősebb LSTM-változatok közül. Rengeteg más is van, mint például a Depth Gated RNN-ek Yao, et al. (2015) által. Van néhány teljesen más megközelítés is a hosszú távú függőségek kezelésére, mint például a Clockwork RNNs by Koutnik, et al. (2014).

Melyik változat a legjobb? Számítanak a különbségek? Greff, et al. (2015) egy szép összehasonlítást végez a népszerű változatokról, és megállapítja, hogy mindegyik nagyjából ugyanolyan. Jozefowicz, et al. (2015) több mint tízezer RNN architektúrát teszteltek, és találtak néhányat, amelyek bizonyos feladatokban jobban működtek, mint az LSTM-ek.

Következtetés

Már korábban említettem, hogy az emberek milyen figyelemre méltó eredményeket érnek el az RNN-ekkel. Lényegében ezeket mind az LSTM-ekkel érik el. Ezek tényleg sokkal jobban működnek a legtöbb feladathoz!

Egyenletek halmazaként leírva az LSTM-ek elég ijesztőnek tűnnek. Remélhetőleg azáltal, hogy ebben az esszében lépésről lépésre végigjártuk őket, egy kicsit megközelíthetőbbé váltak.

A LSTM-ek nagy lépést jelentettek abban, amit az RNN-ekkel elérhetünk. Természetes, hogy elgondolkodunk: van még egy nagy lépés? A kutatók körében elterjedt vélemény az: “Igen! Van egy következő lépés, és ez a figyelem!” Az ötlet lényege, hogy az RNN minden egyes lépése egy nagyobb információgyűjteményből választja ki a vizsgálandó információt. Ha például egy RNN-t arra használunk, hogy egy képet leíró feliratot készítsen, akkor az RNN minden egyes kimeneti szóhoz kiválaszthatja a kép egy részét, amelyet meg kell néznie. Valójában Xu, et al. (2015) pontosan ezt teszi – ez egy szórakoztató kiindulópont lehet, ha a figyelmet szeretné felfedezni! Számos igazán izgalmas eredmény született a figyelem felhasználásával, és úgy tűnik, hogy még sokkal több van a sarkon…

A figyelem nem az egyetlen izgalmas szál az RNN-kutatásban. Például a Kalchbrenner, et al. (2015) által készített Grid LSTM-ek rendkívül ígéretesnek tűnnek. Az RNN-eket generatív modellekben használó munkák – például Gregor, et al. (2015), Chung, et al. (2015) vagy Bayer & Osendorfer (2015) – szintén nagyon érdekesnek tűnnek. Az elmúlt néhány év izgalmas időszak volt a rekurrens neurális hálózatok számára, és az elkövetkezők csak még izgalmasabbnak ígérkeznek!

Köszönet

Hálás vagyok számos embernek, akik segítettek jobban megérteni az LSTM-eket, kommentálták a vizualizációkat, és visszajelzést adtak ehhez a bejegyzéshez.

Hálás vagyok a Google-nál dolgozó kollégáimnak a hasznos visszajelzésekért, különösen Oriol Vinyalsnak, Greg Corradónak, Jon Shlensnek, Luke Vilnisnek és Ilya Sutskevernek. Hálás vagyok sok más barátomnak és kollégámnak is, amiért időt szakítottak rám, köztük Dario Amodeinak és Jacob Steinhardtnak. Különösen hálás vagyok Kyunghyun Chónak az ábráimmal kapcsolatos rendkívül figyelmes levelezésért.

Ezt a bejegyzést megelőzően az LSTM-ek magyarázatát két szemináriumsorozat során gyakoroltam, amelyet a neurális hálózatokról tartottam. Köszönöm mindenkinek, aki ezeken részt vett, az irántam tanúsított türelmét és a visszajelzéseket.

1. A modern LSTM-hez az eredeti szerzőkön kívül sokan hozzájárultak. A nem teljes körű lista a következő: Felix Gers, Fred Cummins, Santiago Fernandez, Justin Bayer, Daan Wierstra, Julian Togelius, Faustino Gomez, Matteo Gagliolo és Alex Graves.

Még több hozzászólás