Most frissítve: 2020. augusztus 18.
Az adatkészletek tartalmazhatnak hiányzó értékeket, és ez számos gépi tanulási algoritmus számára problémát okozhat.
Az előrejelzési feladat modellezése előtt jó gyakorlat a hiányzó értékek azonosítása és pótlása a bemeneti adatok minden oszlopában. Ezt nevezzük hiányzó adatok imputálásának, vagy röviden imputálásnak.
Az adatimputálás népszerű megközelítése az, hogy minden oszlopra kiszámítunk egy statisztikai értéket (például egy átlagot), és az adott oszlop összes hiányzó értékét a statisztikával helyettesítjük. Ez azért népszerű megközelítés, mert a statisztika könnyen kiszámítható a képzési adathalmaz segítségével, és mert gyakran jó teljesítményt eredményez.
Ezzel a bemutatóval felfedezheti, hogyan használhatja a hiányzó adatok statisztikai imputálási stratégiáit a gépi tanulásban.
A bemutató elvégzése után tudni fogja:
- A hiányzó értékeket NaN értékekkel kell jelölni, és statisztikai mértékekkel lehet helyettesíteni az értékek oszlopának kiszámításához.
- Hogyan tölthet be egy hiányzó értékeket tartalmazó CSV-értéket, és jelölheti a hiányzó értékeket NaN-értékekkel, valamint jelentheti a hiányzó értékek számát és százalékos arányát az egyes oszlopokhoz.
- Hogyan imputálhatja a hiányzó értékeket statisztikával, mint adatelőkészítési módszerrel a modellek kiértékelésekor és a végleges modell illesztésekor az új adatokra történő előrejelzésekhez.
Kezdje el projektjét az új könyvemmel Data Preparation for Machine Learning, amely lépésről lépésre bemutató útmutatókat és az összes példa Python forráskódfájlját tartalmazza.
Kezdjük el.
- Frissítve: Jun/2020:

Statistic Imputation for Missing Values in Machine Learning
Photo by Bernal Saborio, some rights reserved.
Tutorial Overview
Ez a tutorial három részre oszlik; ezek a következők:
- Statisztikai imputáció
- Lovak kólikája adathalmaz
- Statisztikai imputáció SimpleImputerrel
- SimpleImputer adattranszformáció
- SimpleImputer és modellértékelés
- A különböző imputált statisztikák összehasonlítása
- SimpleImputer transzformáció előrejelzés készítésekor
.
Statisztikai imputálás
Egy adathalmazban lehetnek hiányzó értékek.
Ezek olyan adatsorok, amelyekben egy vagy több érték vagy oszlop nincs jelen az adott sorban. Az értékek hiányozhatnak teljesen, vagy egy speciális karakterrel vagy értékkel, például egy kérdőjellel “?” jelölve lehetnek.
Ezek az értékek többféleképpen is kifejezhetők. Láttam már őket többek között semmiként , üres karakterláncként , a kifejezett NULL vagy undefined vagy N/A vagy NaN karakterláncként és a 0-ás számként is megjelenni. Nem számít, hogyan jelennek meg az adatkészletében, ha tudja, mire számíthat, és ellenőrzi, hogy az adatok megfelelnek-e ennek az elvárásnak, csökkentheti a problémákat, amikor elkezdi használni az adatokat.
– Page 10, Bad Data Handbook, 2012.
Az értékek számos, gyakran a problématerületre jellemző okból hiányozhatnak, és olyan okok lehetnek, mint a hibás mérések vagy az adatok elérhetetlensége.
Ezek számos okból előfordulhatnak, például a mérőberendezések meghibásodása, a kísérleti elrendezés megváltozása az adatgyűjtés során, valamint több hasonló, de nem azonos adatkészlet összevetése.
– 63. oldal, Adatbányászat: Practical Machine Learning Tools and Techniques, 2016.
A legtöbb gépi tanulási algoritmus numerikus bemeneti értékeket igényel, és az adathalmaz minden sora és oszlopa számára egy értéket. Mint ilyen, a hiányzó értékek problémákat okozhatnak a gépi tanulási algoritmusok számára.
Az adathalmazban a hiányzó értékek azonosítása és numerikus értékkel való helyettesítése gyakori. Ezt nevezzük adatimputálásnak, vagy hiányzó adatok imputálásának.
Az adatimputálás egyszerű és népszerű megközelítése azt jelenti, hogy statisztikai módszerekkel becslünk egy értéket egy oszlopra a jelenlévő értékekből, majd a kiszámított statisztikával helyettesítjük az oszlop összes hiányzó értékét.
Ez azért egyszerű, mert a statisztika gyorsan kiszámítható, és azért népszerű, mert gyakran nagyon hatékonynak bizonyul.
A kiszámított statisztikák közé tartoznak:
- az oszlop átlagértéke.
- az oszlop mediánértéke.
- az oszlop móduszértéke.
- egy konstans érték.
Most, hogy már ismerjük a hiányzó értékek imputálásának statisztikai módszereit, nézzünk meg egy hiányzó értékeket tartalmazó adathalmazt.
Meg akarja kezdeni az adatelőkészítést?
Vegye fel most a 7 napos ingyenes e-mailes gyorstalpaló tanfolyamomat (mintakóddal).
Kattintson a feliratkozáshoz, és kapja meg a tanfolyam ingyenes PDF Ebook változatát is.
Töltse le az INGYENES minitanfolyamát
Lovak kólikája adatállomány
A lovak kólikája adatállomány a kólikás lovak orvosi jellemzőit írja le, valamint azt, hogy éltek-e vagy elpusztultak.
300 sor és 26 input változó van egy output változóval. Ez egy bináris osztályozási előrejelzési feladat, amelynek során azt kell megjósolni, hogy 1, ha a ló élt, és 2, ha a ló meghalt.
Ez az adathalmaz számos olyan mezőt tartalmaz, amelyet kiválaszthatunk az előrejelzéshez. Ebben az esetben azt fogjuk megjósolni, hogy a probléma sebészeti volt-e vagy sem (23-as oszlopindex), így ez egy bináris osztályozási feladat.
Az adathalmaz számos hiányzó értéket tartalmaz számos oszlop esetében, ahol minden hiányzó értéket egy kérdőjel karakterrel (“?”) jelölünk.
Az alábbiakban egy példát mutatunk az adathalmaz soraira, amelyekben megjelölt hiányzó értékek vannak.
|
1
2
3
4
5
|
2,1,530101,38.50,66,28,3,3,?,2,5,4,4,?,?,?,3,5,45.00,8.40,?,?,2,2,11300,00000,00000,2
1,1,534817,39.2,88,20,?,?,4,1,3,4,2,?,?,?,4,2,50,85,2,2,3,2,02208,00000,00000,2
2,1,530334,38.30,40,24,1,1,3,1,3,3,1,?,?,?,1,1,33.00,6.70,?,?,1,2,00000,00000,00000,1
1,9,5290409,39.10,164,84,4,1,6,2,2,4,4,1,2,5.00,3,?,48.00,7.20,3,5.30,2,1,02208,00000,00000,1
…
|
Az adatkészletről itt tudhat meg többet:
- Horse Colic Dataset
- Horse Colic Dataset Description
Nem kell letölteni az adatkészletet, mert a kidolgozott példákban automatikusan letöltjük.
A hiányzó értékek NaN (nem szám) értékkel való jelölése a Python segítségével betöltött adatállományban a legjobb gyakorlat.
Az adatállományt a read_csv() Pandas függvénnyel tölthetjük be, és megadhatjuk a “na_values” értékek betöltéséhez a ‘?’ hiányzóként, NaN értékkel jelölve.
|
1
2
3
4
|
…
# load dataset
url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv’
dataframe = read_csv(url, header=None, na_values=’?’)
|
A betöltés után felülvizsgálhatjuk a betöltött adatokat, hogy megerősítsük, hogy “?” értékek NaN-ként vannak jelölve.
|
1
2
3
|
…
# az első néhány sor összegzése
print(dataframe.head())
|
Ezután felsorolhatjuk az egyes oszlopokat, és jelenthetjük a hiányzó értékeket tartalmazó sorok számát az adott oszlophoz.
|
1
2
3
4
5
6
7
|
…
# összegezze a hiányzó értékeket tartalmazó sorok számát minden oszlopra vonatkozóan
for i in range(dataframe.shape):
# számolja meg a hiányzó értékeket tartalmazó sorok számát
n_miss = dataframe].isnull().sum()
perc = n_miss / dataframe.shape * 100
print(‘> %d, Hiányzó: %d (%.1f%%%)’ % (i, n_miss, perc))
|
Az adatállomány betöltésének és összegzésének teljes példája az alábbiakban található.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
# összefoglalja a lókólika adatállományt
from pandas import read_csv
# load dataset
url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv’
dataframe = read_csv(url, header=None, na_values=’?’)
# összefoglalja az első néhány sort
print(dataframe.head())
# összegezze a hiányzó értékeket tartalmazó sorok számát az egyes oszlopokhoz
for i in range(dataframe.shape):
# számolja meg a hiányzó értékeket tartalmazó sorok számát
n_miss = dataframe].isnull().sum()
perc = n_miss / dataframe.shape * 100
print(‘> %d, Hiányzó: %d (%.1f%%%)’ % (i, n_miss, perc))
|
A példa futtatása először betölti az adatállományt, és összegzi az első öt sort.
Láthatjuk, hogy a “?” karakterrel jelölt hiányzó értékeket NaN értékekkel helyettesítettük.
A következőkben láthatjuk az adatállomány összes oszlopának listáját, valamint a hiányzó értékek számát és százalékos arányát.
Láthatjuk, hogy egyes oszlopokban (pl. az 1. és 2. oszlopindexben) nincs hiányzó érték, míg más oszlopokban (pl. a 15. és 21. oszlopindexben) sok vagy akár a legtöbb hiányzó érték van.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
> 0, Hiányzik:
> 1, Hiányzik: 0 (0,0%)
> 3, Hiányzik: 60 (20,0%)
> 4, Hiányzik: (8,0%)
> 5, Hiányzik: (19,3%)
> 6, Hiányzik: (18,7%)
> 7, Hiányzik: (23,0%)
> 8, Hiányzik: (15,7%)
> 9, Hiányzik: (10,7%)
> 10, Hiányzik: (18,3%)
> 11, Hiányzik: (14,7%)
> 12, Hiányzik: (18,7%)
> 13, Hiányzik: (34,7%)
> 14, Hiányzik: (35,3%)
> 15, Hiányzik: (82,3%)
> 16, Hiányzik: (34,0%)
> 17, Hiányzik: (39,3%)
> 18, Hiányzik: (9,7%)
> 19, Hiányzik: (11,0%)
> 20, Hiányzik: (55,0%)
> 21, Hiányzik: (66,0%)
> 22, Hiányzik: (0 (0,0%)
> 24, Hiányzik: 0 (0,0%)
> 26, Hiányzik: 0 (0.0%)
|
Most, hogy megismerkedtünk a lovak kólikája adathalmazzal, amely hiányzó értékeket tartalmaz, nézzük meg, hogyan használhatjuk a statisztikai imputációt.
Statisztikai imputáció a SimpleImputerrel
A scikit-learn gépi tanulási könyvtár biztosítja a SimpleImputer osztályt, amely támogatja a statisztikai imputációt.
Ebben a részben azt vizsgáljuk meg, hogyan használhatjuk hatékonyan a SimpleImputer osztályt.
SimpleImputer adattranszformáció
A SimpleImputer egy adattranszformáció, amelyet először az egyes oszlopokra kiszámítandó statisztika típusa alapján konfigurálunk, e.pl. mean.
|
1
2
3
|
…
# define imputer
imputer = SimpleImputer(strategy=’mean’)
|
Az imputert ezután illesztjük az adathalmazra, hogy minden oszlopra kiszámítsuk a statisztikát.
|
1
2
3
|
…
# fit az adathalmazon
imputer.fit(X)
|
A fit imputert ezután az adathalmazra alkalmazzuk, hogy létrehozzuk az adathalmaz egy olyan másolatát, amelyben az egyes oszlopok hiányzó értékeit statisztikai értékkel helyettesítjük.
|
1
2
3
|
…
# transzformáljuk az adathalmazt
Xtrans = imputer.transform(X)
|
A használatát a lókólika adathalmazon demonstrálhatjuk, és megerősíthetjük a működését azzal, hogy összegezzük a hiányzó értékek teljes számát az adathalmazban a transzformáció előtt és után.
A teljes példa az alábbiakban található.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
# statisztikai imputáció. transzformáció a lókólika adathalmazhoz
from numpy import isnan
from pandas import read_csv
from sklearn.impute import SimpleImputer
# load dataset
url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv’
dataframe = read_csv(url, header=None, na_values=’?’)
# split into input and output elements
data = dataframe.values
ix = ) if i != 23]
X, y = data, data
# print total missing
print(‘Missing: %d’ % sum(isnan(X).flatten())))
# define imputer
imputer = SimpleImputer(strategy=’mean’)
# fit on the dataset
imputer.fit(X)
# transzformáljuk az adathalmazt
Xtrans = imputer.transform(X)
# nyomtassuk ki a teljes hiányzó mennyiséget
print(‘Missing: %d’ % sum(isnan(Xtrans).flatten())))
|
A példa futtatása először betölti az adatállományt, és az adatállományban a hiányzó értékek teljes számát 1605-nek jelzi.
A transzformáció beállítása, illesztése és végrehajtása megtörtént, és az így kapott új adatállományban nincsenek hiányzó értékek, ami megerősíti, hogy a transzformáció a várt módon történt.
Minden hiányzó értéket az oszlopának átlagértékével helyettesítettünk.
|
1
2
|
Missing: 1605
Missing: 0
|
SimpleImputer and Model Evaluation
Egy jó gyakorlat a gépi tanulási modellek kiértékelése egy adathalmazon k-szoros keresztvalidálással.
A hiányzó adatok statisztikai imputálásának helyes alkalmazásához és az adatszivárgás elkerülése érdekében szükséges, hogy az egyes oszlopokra számított statisztikákat csak a képzési adathalmazon számítsuk ki, majd az adathalmaz minden egyes hajtására alkalmazzuk a képzési és teszthalmazon.
Ha újramintavételezést használunk a hangolási paraméterértékek kiválasztására vagy a teljesítmény becslésére, az imputálást az újramintavételezésbe kell beépíteni.
– Page 42, Applied Predictive Modeling, 2013.
Ez egy olyan modellezési csővezeték létrehozásával érhető el, ahol az első lépés a statisztikai imputálás, majd a második lépés a modell. Ez a Pipeline osztály használatával érhető el.
A lenti Pipeline például egy SimpleImputer “mean” stratégiával, majd egy random forest modellel dolgozik.
|
1
2
3
4
5
|
…
# define modeling pipeline
model = RandomForestClassifier()
imputer = SimpleImputer(strategy=’mean’)
pipeline = Pipeline(steps=)
|
Az átlagot kiértékelhetjük-imputált adathalmazt és a random forest modellező csővezetéket a lókólika-adathalmazra ismételt 10-szeres keresztvalidálással.
A teljes példa az alábbiakban található.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
# evaluate mean imputation and random forestet a lókólika adathalmazra
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.pipeline import Pipeline
# load dataset
url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv’
dataframe = read_csv(url, header=None, na_values=’?’)
# felosztás input és output elemekre
data = dataframe.values
ix = ) if i != 23]
X, y = data, data
# define modeling pipeline
model = RandomForestClassifier()
imputer = SimpleImputer(strategy=’mean’)
pipeline = Pipeline(steps=)
# define model evaluation
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# modell kiértékelése
scores = cross_val_score(pipeline, X, y, scoring=’accuracy’, cv=cv, n_jobs=-1)
print(‘Mean Accuracy: %.3f (%.3f)’ % (mean(scores), std(scores))))
|
A példa futtatása helyesen alkalmazza az adatimputációt a keresztvalidálási eljárás minden egyes hajtására.
Megjegyzés: Az algoritmus vagy az értékelési eljárás sztochasztikus jellege, illetve a numerikus pontosság eltérései miatt az Ön eredményei eltérhetnek. Fontolja meg a példa többszöri futtatását, és hasonlítsa össze az átlagos eredményt.
A csővezeték kiértékelése a 10-szeres kereszt-validálás háromszori ismétlésével történik, és az átlagos osztályozási pontosságot az adathalmazon körülbelül 86-nak jelenti.3 százalékot, ami jó eredmény.
|
1
|
Szintű pontosság: 0,863 (0.054)
|
A különböző imputált statisztikák összehasonlítása
Honnan tudjuk, hogy az “átlagos” statisztikai stratégia használata jó vagy legjobb erre az adathalmazra?
A válasz az, hogy nem tudjuk, és hogy önkényesen választottuk.
Tervezhetünk egy kísérletet az egyes statisztikai stratégiák tesztelésére, és kideríthetjük, hogy melyik működik a legjobban ennél az adathalmaznál, összehasonlítva az átlag, a medián, a módusz (leggyakoribb) és az állandó (0) stratégiákat. Ezután összehasonlíthatjuk az egyes megközelítések átlagos pontosságát.
A teljes példa az alábbiakban található.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
# összehasonlít. statisztikai imputációs stratégiák a lókólika adathalmazhoz
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.pipeline import Pipeline
from matplotlib import pyplot
# load dataset
url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv’
dataframe = read_csv(url, header=None, na_values=’?’)
# felosztás input és output elemekre
data = dataframe.values
ix = ) if i != 23]
X, y = data, data
# értékeljük ki az egyes stratégiákat az adathalmazon
results = list()
strategies =
for s in strategies:
# hozzuk létre a modellező csővezetéket
pipeline = Pipeline(steps=)
# értékeljük ki a modellt
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(pipeline, X, y, scoring=’accuracy’, cv=cv, n_jobs=-1)
# eredmények tárolása
results.append(scores)
print(‘>%s %.3f (%.3f)’ % (s, mean(scores), std(scores))))
# ábrázolja a modell teljesítményét az összehasonlításhoz
pyplot.boxplot(results, labels=strategies, showmeans=True)
pyplot.show()
|
A példa futtatása az egyes statisztikai imputációs stratégiákat értékeli a lókólika adathalmazon ismételt keresztvalidálással.
Figyelem: Az algoritmus vagy az értékelési eljárás sztochasztikus jellege, illetve a numerikus pontosságban mutatkozó különbségek miatt az Ön eredményei eltérhetnek. Fontolja meg a példa többszöri futtatását, és hasonlítsa össze az átlagos eredményt.
Az egyes stratégiák átlagos pontosságát útközben közöljük. Az eredmények azt mutatják, hogy egy konstans érték, például 0 használata a legjobb teljesítményt, körülbelül 88,1 százalékot eredményez, ami kiemelkedő eredmény.
|
1
2
3
4
|
>átlag 0.860 (0.054)
>medián 0.862 (0.065)
>most_frequent 0,872 (0,052)
>constant 0,881 (0,047)
|
A futtatás végén minden eredménykészlethez elkészül egy box and whisker plot, amely lehetővé teszi az eredmények eloszlásának összehasonlítását.
Jól látható, hogy az állandó stratégia pontossági eredményeinek eloszlása jobb, mint a többi stratégiáé.
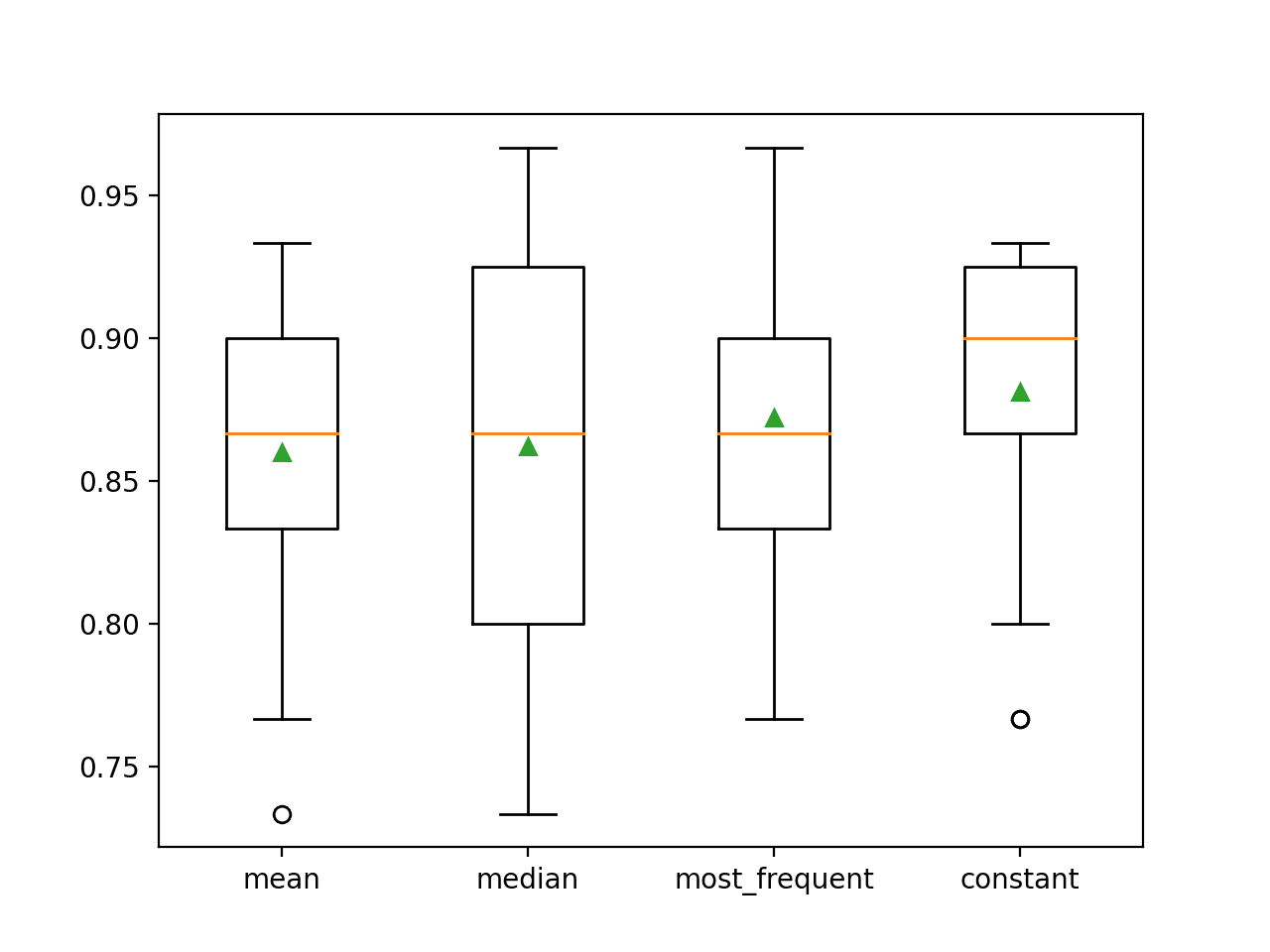
Box and Whisker Plot of Statistical Imputation Strategies Applied to the Horse Colic Dataset
SimpleImputer Transform When Making a Prediction
Elképzelhető, hogy a konstans imputációs stratégiával és a random forest algoritmussal létrehozunk egy végleges modellező csővezetéket, majd új adatokra készítünk előrejelzést.
Ezt úgy érhetjük el, hogy definiáljuk a csővezetéket és illesztjük az összes rendelkezésre álló adatra, majd az új adatokat argumentumként átadva meghívjuk a predict() függvényt.
Fontos, hogy az új adatok sorában a hiányzó értékeket NaN értékkel kell jelölni.
|
1
2
3
|
…
# define new data
row =
|
A teljes példa az alábbiakban található.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
# konstans imputáció. stratégia és predikció a tömlőkólika adathalmazhoz
from numpy import nan
from pandas import read_csv
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.pipeline import Pipeline
# load dataset
url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv’
dataframe = read_csv(url, header=None, na_values=’?’)
# split into input and output elements
data = dataframe.values
ix = ) if i != 23]
X, y = data, data
# hozzuk létre a modellező csővezetéket
pipeline = Pipeline(steps=)
# illesszük a modellt
pipeline.fit(X, y)
# új adatok definiálása
row =
# előrejelzés készítése
yhat = pipeline.predict()
# összegezze az előrejelzést
print(‘Predicted Class: %d’ % yhat)
|
A példa futtatása illeszkedik a modellező csővezetékhez az összes rendelkezésre álló adaton.
Egy új adatsort definiál a hiányzó értékeket NaN-nal jelölve, és osztályozási előrejelzést készít.
|
1
|
Predicted Class: 2
|
További olvasmányok
Ez a rész további forrásokat tartalmaz a témában, ha mélyebben szeretnél elmélyülni.
Related Tutorials
- Results for Standard Classification and Regression Machine Learning Datasets
- How to Handle Missing Data with Python
Books
- Bad Data Handbook, 2012.
- Data Mining: Practical Machine Learning Tools and Techniques, 2016.
- Applied Predictive Modeling, 2013.
APIs
- Imputation of missing values, scikit-learn Documentation.
- sklearn.impute.SimpleImputer API.
Dataset
- Horse Colic Dataset
- Horse Colic Dataset Description
Summary
Ebben a bemutatóban felfedezte, hogyan használhatunk statisztikai imputációs stratégiákat hiányzó adatokra a gépi tanulásban.
Közelebbről megtanulta:
- A hiányzó értékeket NaN értékekkel kell jelölni, és statisztikai mértékekkel lehet helyettesíteni az értékek oszlopának kiszámításához.
- Hogyan töltsön be egy hiányzó értékeket tartalmazó CSV-értéket, és jelölje a hiányzó értékeket NaN értékekkel, valamint jelentse a hiányzó értékek számát és százalékos arányát minden oszlophoz.
- Hogyan imputálja a hiányzó értékeket statisztikával mint adatelőkészítési módszerrel a modellek kiértékelésekor és a végleges modell illesztésekor az új adatokra vonatkozó előrejelzések készítéséhez.
Kérdése van?
Tegye fel kérdéseit az alábbi megjegyzésekben, és igyekszem a lehető legjobban válaszolni.
Kezdje meg a modern adatelőkészítést!

Prepare your machine learning data in minutes
….mindössze néhány sor python kóddal
Fedezze fel, hogyan az új Ebookomban:
Adatelőkészítés a gépi tanuláshoz
Elhelyezi az önképző tananyagot teljes működő kóddal:
Feature Selection, RFE, Data Cleaning, Data Transforms, Scaling, Dimensionality Reduction, és még sok más…
Modern adatelőkészítési technikák alkalmazása
a gépi tanulási projektjeiben
Nézze meg, mi van benne
.