Pont-szimmetria akkor áll fenn, ha az ábrát egyetlen pont köré rajzoljuk.

Ezt a pontot az ábra középpontjának vagy a szimmetria középpontjának nevezzük. A mellékelt ábrán megfigyelhetjük, hogy az ábrán lévő X pontnak megfelelően létezik egy X’ pont a középpont másik oldalán, amely közvetlenül szemben van X-szel, és az ábrán fekszik. Azt mondjuk, hogy az ábra a középpont körül szimmetrikus.
Megjegyzés:
Ha egy ábrát 180°-kal elforgatunk, és visszanyeri eredeti alakját,akkor azt mondjuk, hogy az ábrán pont-szimmetria van.
Példák a pont-szimmetriát mutató ábrákra:
● Az angol ábécé összes betűje.
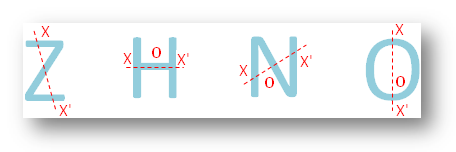
● Különböző geometriai alakzatok.
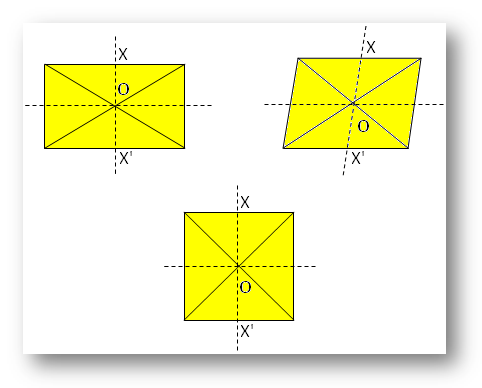
Jegyzet:
Itt O a szimmetriaközpont.
X tekintetében létezik olyan X’, hogy X’ közvetlenül szemben van X-szel az O másik oldalán.
Melyek azok a feltételek, amelyeknek egy alakzat vagy egy ábra megfelel a pontszimmetriához?
A feltételek, amelyeknek egy alakzat vagy egy ábra megfelel a pontszimmetriához, azaz minden résznek legyen egy megfelelő része
– a távolságnak egyenlőnek kell lennie a középponttól
– de ellentétes irányúnak kell lennie.
● Kapcsolódó fogalmak
● Lineáris szimmetria
● Szimmetriavonalak
● Forgásszimmetria
● Forgásszimmetria rendje
● A szimmetria típusai
● Tükrözés
● Egy pont tükrözése az x-tengelyen
● Egy pont tükrözése az y- tengelyen
● Egy pont tükrözése az y-tengelyen
● Egy pont tükrözése az origóban
● Forgatás
● 90 fokos forgatás az óramutató járásával megegyező irányban
● 90 fokos forgatás az óramutató járásával ellentétes irányban
● 180 fokos forgatás
.
7. osztályos matematika feladatok
8. osztályos matematika gyakorlat
Pontszimmetriától a HOME PAGE-ig