Bevezetés
Képzelje el – Önt a következő iPhone árának előrejelzésével bízták meg, és történelmi adatokkal látták el. Ezek olyan jellemzőket tartalmaznak, mint a negyedéves eladások, a havi kiadások és egy sor olyan dolog, ami az Apple mérlegéhez tartozik. Mint adattudós, milyen típusú problémának minősítenéd ezt? Természetesen az idősor-modellezéshez.
A termékeladások előrejelzésétől kezdve a háztartások villamosenergia-felhasználásának becsléséig az idősor-előrejelzés az egyik alapvető készség, amelyet minden adattudósnak ismernie, ha nem is elsajátítania kell. Rengeteg különböző technika létezik, amelyeket használhat, és ebben a cikkben az egyik leghatékonyabbat, az Auto ARIMA nevű technikát fogjuk tárgyalni.

Megértjük először az ARIMA fogalmát, ami elvezet minket a fő témánkhoz – az Auto ARIMA-hoz. Hogy megszilárdítsuk a fogalmainkat, felveszünk egy adatkészletet, és implementáljuk azt Pythonban és R-ben egyaránt.
Tartalomjegyzék
- Mi az idősor?
- Az idősoros előrejelzés módszerei
- Elvezetés az ARIMA-hoz
- Lépések az ARIMA megvalósításához
- Miért van szükségünk AutoARIMA-ra?
- Auto ARIMA megvalósítása (légi utasok adathalmazán)
- Hogyan választja ki az auto ARIMA a paramétereket?
Ha már ismeri az idősorokat és azok technikáit (mint a mozgóátlag, az exponenciális simítás és az ARIMA), akkor közvetlenül a 4. szakaszra ugorhat. Kezdők számára az alábbi szakaszt ajánljuk, amely röviden bemutatja az idősorokat és a különböző előrejelzési technikákat.
Mi az idősor?
Mielőtt megismernénk az idősoros adatokkal való munka technikáit, először is meg kell értenünk, mi is valójában az idősor, és miben különbözik bármely más adattípustól. Íme az idősor hivatalos definíciója: – Az idősor következetes időközönként mért adatpontok sorozata. Ez egyszerűen azt jelenti, hogy bizonyos értékeket állandó időközönként rögzítenek, ami lehet óránkénti, napi, heti, 10 naponkénti és így tovább. Az idősorokat az különbözteti meg, hogy a sorozat minden egyes adatpontja függ az előző adatpontoktól. Értsük meg a különbséget világosabban néhány példán keresztül.
1. példa:
Tegyük fel, hogy van egy adathalmazunk azokról az emberekről, akik hitelt vettek fel egy adott cégtől (az alábbi táblázatban látható módon). Gondolja, hogy az egyes sorok kapcsolódnak az előző sorokhoz? Biztosan nem! A személy által felvett hitel az anyagi körülményein és igényein alapul (lehetnek más tényezők is, mint például a család mérete stb., de az egyszerűség kedvéért csak a jövedelmet és a hiteltípust vesszük figyelembe) . Emellett az adatokat nem egy adott időintervallumban gyűjtötték. Attól függ, hogy a vállalat mikor kapott kölcsönkérelmet.

2. példa:
Vegyünk egy másik példát. Tegyük fel, hogy van egy adatkészletünk, amely a levegő CO2-szintjét tartalmazza naponta (alábbi képernyőkép). Képes lesz megjósolni a következő nap megközelítő CO2-mennyiségét az elmúlt napok értékei alapján? Hát persze. Ha megfigyeled, az adatokat naponta rögzítették, vagyis az időintervallum állandó (24 óra).

Mostanra már biztosan van egy megérzésed erről – az első eset egy egyszerű regressziós probléma, a második pedig egy idősoros probléma. Bár az idősoros feladvány itt is megoldható lineáris regresszióval, de ez nem igazán a legjobb megközelítés, mivel elhanyagolja az értékeknek az összes relatív múltbeli értékkel való kapcsolatát. Most nézzük meg az idősoros problémák megoldására használt néhány gyakori technikát.
Az idősoros előrejelzés módszerei
Az idősoros előrejelzésnek számos módszere van, és ebben a részben röviden foglalkozunk velük. Az alább említett technikák részletes magyarázata és python kódjai megtalálhatók ebben a cikkben:
- Naiv megközelítés: Ebben az előrejelzési technikában az új adatpont értékét az előző adatponttal megegyezőnek jósoljuk. Az eredmény egy lapos vonal lenne, mivel minden új érték az előző értékeket veszi át.
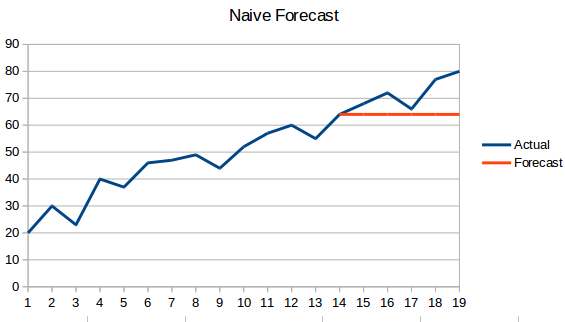
- Egyszerű átlag: A következő értéket az összes korábbi érték átlagaként vesszük. Az előrejelzések itt jobbak, mint a “naiv megközelítés”, mivel nem eredményez lapos vonalat, de itt az összes korábbi értéket figyelembe veszi, ami nem mindig hasznos. Például, ha a mai hőmérsékletet kell megjósolni, akkor az elmúlt 7 nap hőmérsékletét kell figyelembe venni, nem pedig az egy hónappal ezelőtti hőmérsékletet.

- Mozgóátlag : Ez egy előrelépés az előző technikához képest. Ahelyett, hogy az összes korábbi pont átlagát vennénk, az ‘n’ korábbi pont átlagát vesszük az előre jelzett értéknek.

- Súlyozott mozgóátlag : A súlyozott mozgóátlag olyan mozgóátlag, ahol a múltbeli ‘n’ értéket különböző súlyokkal súlyozzuk.

- Egyszerű exponenciális simítás : Ebben a technikában a közelmúltbeli megfigyelésekhez nagyobb súlyokat rendelünk, mint a távoli múltbeli megfigyelésekhez.

- Holt lineáris trendmodellje: Ez a módszer figyelembe veszi az adathalmaz trendjét. Trend alatt a sorozatok növekvő vagy csökkenő jellegét értjük. Tegyük fel, hogy egy szállodában a foglalások száma minden évben növekszik, akkor azt mondhatjuk, hogy a foglalások száma növekvő trendet mutat. Az előrejelzési függvény ebben a módszerben a szint és a trend függvénye.

- Holt Winters módszer: Ez az algoritmus figyelembe veszi a sorozat trendjét és szezonalitását is. Például – egy szállodában a foglalások száma hétvégén magas & hétköznapokon alacsony, és minden évben növekszik; létezik egy heti szezonalitás és egy növekvő trend.

- ARIMA: Az ARIMA egy nagyon népszerű technika az idősorok modellezésére. Az adatpontok közötti korrelációt írja le, és figyelembe veszi az értékek különbségét. Az ARIMA továbbfejlesztése a SARIMA (vagy szezonális ARIMA). Az ARIMA-t a következő részben egy kicsit részletesebben fogjuk megvizsgálni.
Elvezetés az ARIMA-ba
Ebben a részben egy gyors bevezetést fogunk tenni az ARIMA-ba, ami hasznos lesz az Auto Arima megértéséhez. Az Arima, a paraméterek (p,q,d), a plotok (ACF PACF) és a végrehajtás részletes magyarázatát tartalmazza ez a cikk : Teljes útmutató az idősorokhoz.
Az ARIMA egy nagyon népszerű statisztikai módszer az idősoros előrejelzéshez. Az ARIMA az Auto-Regresszív Integrált Mozgó Átlagok rövidítése. Az ARIMA modellek a következő feltételezések alapján működnek –
- Az adatsor stacionárius, ami azt jelenti, hogy az átlag és a variancia nem változhat az idővel. A sorozatot log-transzformációval vagy a sorozat differenciálásával lehet stacionáriussá tenni.
- A bemenetként megadott adatoknak egyváltozós sorozatoknak kell lenniük, mivel az arima a múltbeli értékeket használja a jövőbeli értékek előrejelzésére.
Az ARIMA három összetevőből áll: AR (autoregresszív kifejezés), I (differenciáló kifejezés) és MA (mozgóátlag kifejezés). Értsük meg az egyes komponenseket –
- Az AR kifejezés a múltbeli értékekre utal, amelyeket a következő érték előrejelzésére használunk. Az AR-termet az arima ‘p’ paramétere határozza meg. A ‘p’ értékét a PACF-diagram segítségével határozzuk meg.
- MA kifejezés a jövőbeli értékek előrejelzéséhez használt múltbeli előrejelzési hibák számának meghatározására szolgál. Az arima “q” paramétere az MA-termet jelöli. Az ACF-diagramot a helyes ‘q’ érték meghatározására használják.
- A differenciálás sorrendje megadja, hogy a differenciálási műveletet hányszor kell elvégezni a sorozatokon, hogy azok stacionáriussá váljanak. Az olyan tesztek, mint az ADF és a KPSS használhatók annak meghatározására, hogy a sorozat stacionárius-e, és segítenek a d érték azonosításában.
Lépések az ARIMA megvalósításához
Az ARIMA modell megvalósításának általános lépései: –
- Az adatok betöltése: A modellépítés első lépése természetesen az adatállomány betöltése
- Előfeldolgozás: Az adatkészlettől függően kerülnek meghatározásra az előfeldolgozás lépései. Ez magában foglalja az időbélyegek létrehozását, a dátum/idő oszlop dtípusának átalakítását, a sorozatok egyváltozóssá tételét stb.
- Sorozatok állandósítása: A feltételezés teljesítése érdekében a sorozatot stacionáriussá kell tenni. Ez magában foglalja a sorozat stacionaritásának ellenőrzését és a szükséges transzformációk elvégzését
- A d értékének meghatározása: A sorozat stacionáriussá tételéhez a különbségművelet elvégzésének számát vesszük d értéknek
- ACF és PACF ábrák készítése: Ez a legfontosabb lépés az ARIMA megvalósításában. Az ACF PACF ábrákat az ARIMA modellünk bemeneti paramétereinek meghatározására használjuk
- Meghatározzuk a p és q értékeket: Olvassuk be a p és q értékeit az előző lépés ábráiból
- Fit ARIMA model: A feldolgozott adatok és az előző lépésekből kiszámított paraméterértékek felhasználásával illessze az ARIMA-modellt
- Jósolja meg az értékeket a validációs halmazon: A jövőbeli értékek előrejelzése
- RMSE kiszámítása: A modell teljesítményének ellenőrzéséhez ellenőrizze az RMSE értékét a validációs készlet előrejelzéseinek és tényleges értékeinek felhasználásával
Miért van szükségünk Auto ARIMA-ra?
Bár az ARIMA egy nagyon hatékony modell az idősoros adatok előrejelzésére, az adatelőkészítési és paraméterhangolási folyamatok végül nagyon időigényesek. Az ARIMA megvalósítása előtt stacionáriussá kell tennünk a sorozatot, és a fentebb tárgyalt ábrák segítségével meg kell határoznunk a p és q értékeit. Az Auto ARIMA igazán egyszerűvé teszi számunkra ezt a feladatot, mivel kiküszöböli az előző részben látott 3-6. lépést. Az alábbiakban az auto ARIMA végrehajtásához szükséges lépéseket kell követnie:
- Töltse be az adatokat: Ez a lépés ugyanaz lesz. Töltse be az adatokat a notebookjába
- Az adatok előfeldolgozása: A bemenetnek egyváltozósnak kell lennie, ezért dobja el a többi oszlopot
- Fit Auto ARIMA: Fit the model on the univariate series
- Predict values on validation set: Előrejelzések készítése a validációs halmazon
- RMSE kiszámítása: A modell teljesítményének ellenőrzése az előre jelzett értékek és a tényleges értékek összehasonlításával
A p és q jellemző kiválasztását, mint látható, teljesen megkerültük. Micsoda megkönnyebbülés! A következő részben az auto ARIMA-t egy játékadatkészlet segítségével fogjuk megvalósítani.
Implementáció Pythonban és R-ben
Az International-Air-Passage adatkészletet fogjuk használni. Ez az adatkészlet az utasok számának havi összegét tartalmazza (ezerben). Két oszlopa van – a hónap és az utasok száma. Az adatkészlet letölthető erről a linkről.
#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)
output -76.51355764316357
Az alábbiakban az R kód ugyanerre a problémára:
# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)
Hogyan választja ki az Auto Arima a legjobb paramétereket
A fenti kódban egyszerűen a .fit() parancsot a modell illesztésére anélkül, hogy ki kellett volna választanunk a p, q, d kombinációt. De hogyan találta ki a modell e paraméterek legjobb kombinációját? Az Auto ARIMA a paraméterek legjobb kombinációjának meghatározásához figyelembe veszi a generált AIC- és BIC-értékeket (ahogy a kódban is látható). Az AIC (Akaike Information Criterion) és a BIC (Bayesian Information Criterion) értékek a modellek összehasonlítására szolgáló becslők. Minél alacsonyabbak ezek az értékek, annál jobb a modell.
Nézze meg ezeket a linkeket, ha érdekli az AIC és BIC mögötti matematika.
Végjegyzetek és további olvasnivalók
Az auto ARIMA-t találtam a legegyszerűbb technikának az idősor-előrejelzés elvégzésére. Egy rövidítés ismerete jó, de a mögötte álló matematika ismerete is fontos. Ebben a cikkben átfutottam az ARIMA működésének részleteit, de mindenképpen nézze át a cikkben megadott linkeket. A könnyű hivatkozás érdekében itt vannak a linkek ismét:
- A Comprehensive Guide for beginners to Time Series Forecast in Python
- Complete Tutorial to Time series in R
- 7 techniques for time series forecasting (with python codes)
Az itt tanultakat ezen a gyakorlati problémán javasolnám gyakorolni: Time Series Practice Problem. Ugyanerre a gyakorlati problémára létrehozott tanfolyamunkat is elvégezheted: Idősoros előrejelzés, hogy előnyt biztosítsunk számodra.