Három példát ismertetünk az élettudományokból: egyet a fizikából, egyet a genetikával kapcsolatban, egyet pedig egy egérkísérletből. Ezek nagyon különbözőek, mégis végül ugyanazt a statisztikai technikát használjuk: lineáris modellek illesztését. A lineáris modelleket jellemzően a mátrixalgebra nyelvén tanítják és írják le.
Motiváló példák
Zuhanó tárgyak
Képzeljük el, hogy a 16. században Galilei helyében egy zuhanó tárgy sebességét próbáljuk leírni. Egy asszisztens felmászik a pisai toronyra, és elejt egy golyót, miközben több másik asszisztens különböző időpontokban rögzíti a helyzetet. Szimuláljunk néhány adatot a ma ismert egyenletekkel és némi mérési hiba hozzáadásával:
set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##metersA segédek átadják az adatokat Galileinek, és ő ezt látja:
mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")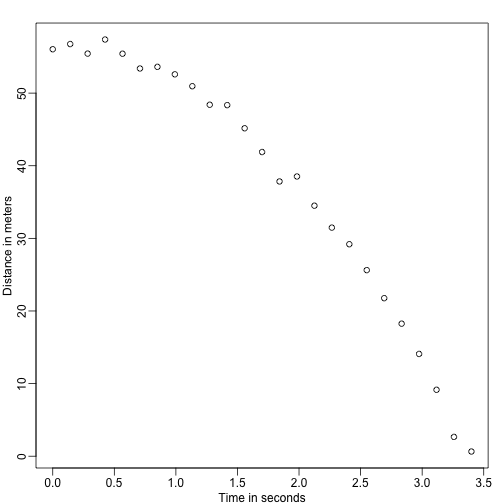
A pontos egyenletet nem tudja, de a fenti ábrát nézve arra következtet, hogy a helyzetnek egy parabolát kell követnie. Így modellezi az adatokat:
Mivel reprezentálja a helyet, reprezentálja az időt, és figyelembe veszi a mérési hibát. Ez egy lineáris modell, mert ismert mennyiségek (th s), amelyeket prediktoroknak vagy kovariánsoknak nevezünk, és ismeretlen paraméterek (az s) lineáris kombinációja.
Apa & fiú magassága
Tegyük fel, hogy Ön Francis Galton a 19. században, és párosított magassági adatokat gyűjt apákról és fiúkról. Azt gyanítja, hogy a magasság öröklődik. Az adataid:
library(UsingR)x=father.son$fheighty=father.son$sheighta következőképpen néznek ki:
plot(x,y,xlab="Father's height",ylab="Son's height")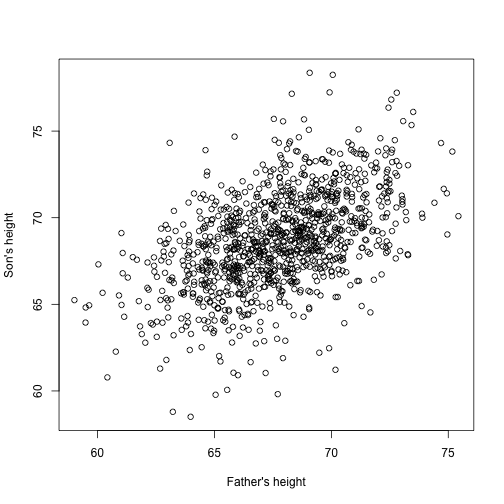
A fiúk magassága valóban lineárisan növekszik az apák magasságával. Ebben az esetben az adatokat leíró modell a következő:
Ez is egy lineáris modell, amelyben a és , az apa, illetve a fiú magassága a -ik párra vonatkozóan, valamint egy, az extra változékonyságot figyelembe vevő kifejezés szerepel. Itt úgy gondoljuk, hogy az apák magassága a prediktor, és fix (nem véletlenszerű), ezért kisbetűket használunk. A mérési hiba önmagában nem tudja megmagyarázni a . Ennek van értelme, mivel vannak más változók is, amelyek nem szerepelnek a modellben, például az anyák magassága, genetikai véletlenszerűség és környezeti tényezők.
Véletlen minták több populációból
Itt olyan egerek testsúlyadatait olvassuk be, amelyeket két különböző étrenddel tápláltak: magas zsírtartalmú és kontroll (chow) étrenddel. Mindkettőből 12 egérből álló véletlen mintánk van. Arra vagyunk kíváncsiak, hogy az étrendnek van-e hatása a testsúlyra. Íme az adatok:
dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")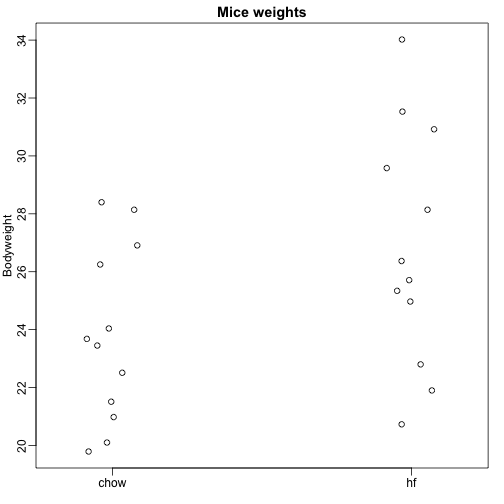
A populációk közötti átlagos súlykülönbséget szeretnénk megbecsülni. Bemutattuk, hogyan tehetjük ezt t-próbák és konfidenciaintervallumok segítségével, a mintaátlagok különbsége alapján. Ugyanezeket a pontos eredményeket kaphatjuk lineáris modellel:
a chow-diéta átlagsúlyával, az átlagok közötti különbséggel, ha az egér magas zsírtartalmú (hf) étrendet kap, ha chow-diétát, és magyarázza az azonos populációhoz tartozó egerek közötti különbségeket.
Lineáris modellek általában
Három nagyon különböző példát láttunk, amelyekben lineáris modelleket használhatunk. Egy általános modell, amely magában foglalja az összes fenti példát, a következő:
Megjegyezzük, hogy a prediktorok általános száma . A mátrixalgebra kompakt nyelvet és matematikai keretet biztosít a fenti keretbe illeszkedő bármely lineáris modellel való számításhoz és levezetéshez.
Paraméterek becslése
A fenti modellek hasznosságához meg kell becsülnünk az ismeretlen s-t. Az első példában egy olyan fizikai folyamatot szeretnénk leírni, amelyre nem lehetnek ismeretlen paramétereink. A második példában az öröklődést értjük meg jobban, ha megbecsüljük, hogy az apa magassága átlagosan mennyire befolyásolja a fiú magasságát. Az utolsó példában azt akarjuk meghatározni, hogy valóban van-e különbség: ha .
A tudományban szokásos megközelítés az, hogy megkeressük azokat az értékeket, amelyek minimalizálják az illesztett modell és az adatok távolságát. A következőt a legkisebb négyzetek (LS) egyenletének nevezzük, és ebben a fejezetben gyakran találkozunk majd vele:
Ha megtaláltuk a minimumot, az értékeket a legkisebb négyzetek becsléseinek (LSE) nevezzük, és a . A becsléseknél a legkisebb négyzet egyenlet kiértékelésekor kapott mennyiséget a maradék négyzetek összegének (RSS) nevezzük. Mivel mindezek a mennyiségek függnek a , ezek véletlen változók. Az s véletlen változók, és végül következtetést fogunk végezni rajtuk.
A zuhanó tárgy példája újra
A középiskolai fizikatanáromnak köszönhetően tudom, hogy egy zuhanó tárgy röppályájának egyenlete:
mivel és a kezdő magasság és sebesség. A fent szimulált adatok ezt az egyenletet követték, és hozzáadtuk a mérési hibát, hogy szimuláljuk a n megfigyeléseket a labda leejtésére a pisai toronyból . Ezért ezt a kódot használtuk az adatok szimulálásához:
g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)Íme, így néznek ki az adatok, ahol a folytonos vonal a valódi pályát jelöli:
plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)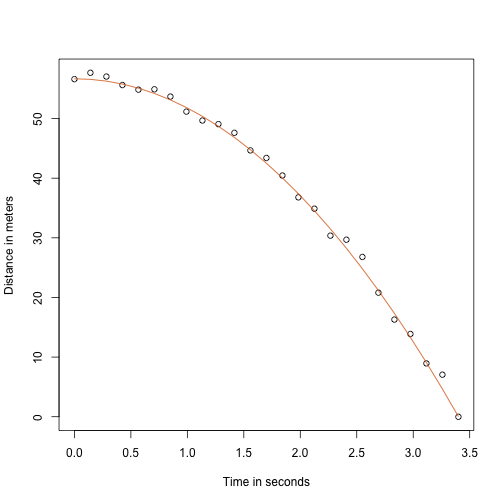
De mi Galileinek tettettük magunkat, ezért nem ismerjük a modell paramétereit. Az adatok azonban arra utalnak, hogy ez egy parabola, így ekként modellezzük:
Hogyan találjuk meg az LSE-t?
A lm függvénnyel
Az R-ben egyszerűen a lm függvény segítségével illeszthetjük ezt a modellt. Ezt a függvényt később részletesen ismertetni fogjuk, de íme egy előzetes:
tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17Az LSE-t, valamint a standard hibákat és a p-értékeket adja meg nekünk.
Az ebben a fejezetben részben elmagyarázzuk a függvény mögötti matematikát.
A legkisebb négyzetek becslése (LSE)
Írjunk egy függvényt, amely kiszámítja az RSS-t bármely vektorra :
rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}Így bármely háromdimenziós vektorra megkapjuk az RSS-t. Íme egy grafikon az RSS függvényében, amikor a másik kettőt fixen tartjuk:
Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)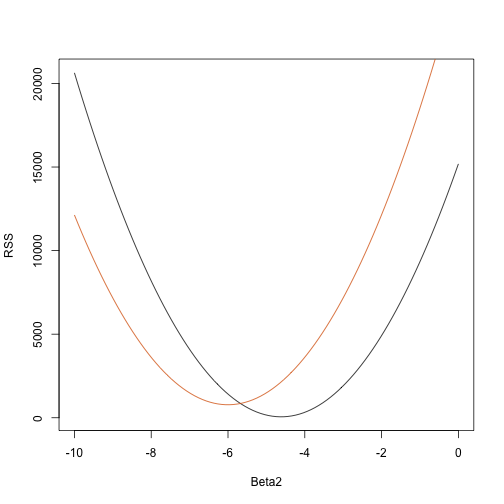
A próbálkozás és hiba itt nem fog működni. Ehelyett használhatjuk a számítást: vegyük a parciális deriváltakat, állítsuk őket 0-ra és oldjuk meg. Természetesen, ha sok paraméterünk van, ezek az egyenletek meglehetősen bonyolulttá válhatnak. A lineáris algebra kompakt és általános megoldást kínál erre a problémára.
Még több Galtonról (haladó)
Az apa-fiú adatok tanulmányozása során Galton egy lenyűgöző felfedezést tett a feltáró elemzés segítségével.
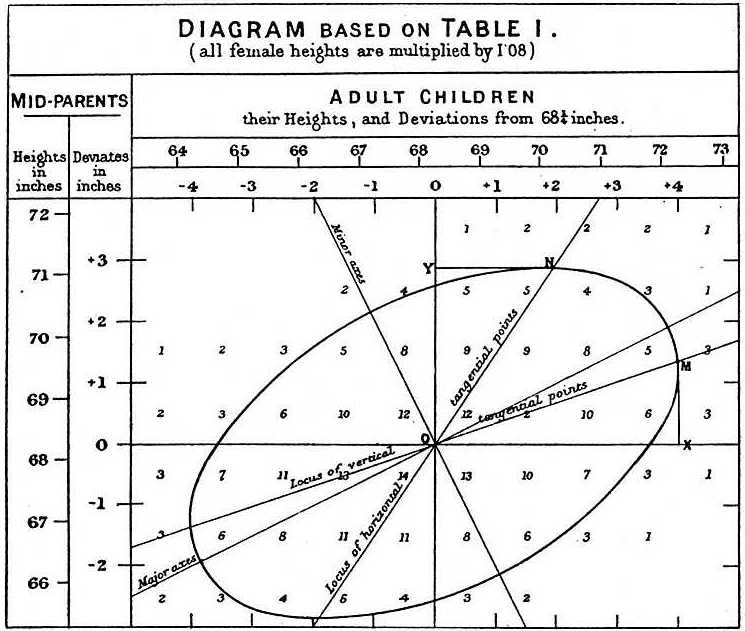
Megfigyelte, hogy ha táblázatba írja az apa-fiú magasságpárok számát, és a táblázatban az azonos összegekkel rendelkező x,y értékeket követi, azok ellipszist alkotnak. A fenti, Galton által készített ábrán látható a 3 esettel rendelkező párok által alkotott ellipszis. Ez aztán ahhoz vezetett, hogy modellezzük ezeket az adatokat korrelált kétváltozós normálisként, amelyet korábban leírtunk:
Elmondtuk, hogyan használhatjuk a matematikát, hogy megmutassuk, hogy ha fixen tartjuk (feltétel, hogy ) az eloszlása normális eloszlású, átlaggal: és szórással . Megjegyezzük, hogy a és közötti korreláció , ami azt jelenti, hogy ha rögzítjük , valójában egy lineáris modellt követ. Az és paraméterek a mi egyszerű lineáris modellünkben kifejezhetők a , és .
kifejezésekkel.