Erősítéses tanulás 101

A megerősítéses tanulás (RL) az egyik legforróbb kutatási téma a modern mesterséges intelligencia területén, és népszerűsége egyre csak növekszik. Lássunk 5 hasznos dolgot, amit tudnunk kell ahhoz, hogy belevágjunk az RL-be.

A megerősítéses tanulás(RL) egyfajta gépi tanulási technika, amely lehetővé teszi egy ágens számára, hogy egy interaktív környezetben próbálgatással tanuljon a saját cselekvéseiből és tapasztalataiból származó visszajelzések felhasználásával.

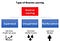
Noha mind a felügyelt, mind a megerősítéses tanulás a bemenet és a kimenet közötti leképezést használja, a felügyelt tanulástól eltérően, ahol az ágensnek adott visszajelzés a feladat végrehajtásához szükséges helyes cselekvéssorozat, a megerősítéses tanulás jutalmakat és büntetéseket használ a pozitív és negatív viselkedés jeleként.

A felügyelet nélküli tanuláshoz képest a megerősítéses tanulás a célok tekintetében különbözik. Míg a felügyelet nélküli tanulásnál a cél az adatpontok közötti hasonlóságok és különbségek megtalálása, addig a megerősítéses tanulás esetében a cél a megfelelő cselekvési modell megtalálása, amely maximalizálja az ágens összesített kumulatív jutalmát. Az alábbi ábra egy általános RL modell akció-visszatérítési hurokját szemlélteti.

Hogyan fogalmazzunk meg egy alapvető megerősítéses tanulási problémát?

Az RL-probléma alapvető elemeit leíró néhány kulcsfogalom a következő:

1. Környezet – Fizikai világ, amelyben az ágens működik
2. Állapot – Az ágens aktuális helyzete
3. Jutalom – Visszajelzés a környezetből
4. Szabályzat – Az ágens állapotát cselekvésekhez leképező módszer
5. Érték – Az a jövőbeli jutalom, amelyet az ágens egy adott állapotban végrehajtott cselekvésért kapna

Egy RL-probléma leginkább játékokon keresztül magyarázható. Vegyük a PacMan játékot, ahol az ágens(PacMan) célja, hogy a rácson lévő ételt megegye, miközben elkerüli az útjába kerülő szellemeket. Ebben az esetben a rácsvilág az ágens interaktív környezete, ahol cselekszik. Az ágens jutalmat kap az étel elfogyasztásáért, és büntetést, ha a szellem megöli (elveszíti a játékot). Az állapotok az ágens helyét jelentik a rácsvilágban, az összesített kumulatív jutalom pedig az, hogy az ágens megnyeri a játékot.

Az optimális politika kialakításához az ágensnek azzal a dilemmával kell szembenéznie, hogy új állapotokat fedezzen fel, ugyanakkor maximalizálja az összesített jutalmát. Ezt nevezzük felfedezés vs. kihasználás kompromisszumnak. A kettő egyensúlyának megteremtése érdekében a legjobb átfogó stratégia rövid távú áldozatokkal járhat. Ezért az ágensnek elegendő információt kell gyűjtenie ahhoz, hogy a jövőben a legjobb átfogó döntést hozza meg.

A Markov-döntési folyamatok (MDP-k) matematikai keretrendszerek a környezet leírására az RL-ben, és szinte minden RL-probléma megfogalmazható MDP-k segítségével. Egy MDP a környezet S véges állapotainak halmazából, az egyes állapotokban lehetséges A(s) cselekvések halmazából, egy valós értékű R(s) jutalomfüggvényből és egy P(s’, s | a) átmeneti modellből áll. A valós környezetben azonban nagyobb valószínűséggel nincs előzetes tudás a környezet dinamikájáról. Ilyen esetekben jól jönnek a modellmentes RL módszerek.

A Q-tanulás egy általánosan használt modellmentes megközelítés, amely egy önjátszó PacMan-ügynök létrehozására használható. A Q-értékek frissítésének fogalma körül forog, amely az a cselekvés elvégzésének értékét jelöli az s állapotban. A következő értékfrissítési szabály a Q-tanulási algoritmus lényege.

Itt egy videó bemutató egy PacMan-ügynökről, amely mély megerősítéses tanulást használ.

Melyek a leggyakrabban használt megerősítéses tanulási algoritmusok?

A Q-tanulás és a SARSA (State-Action-Reward-State-Action) két gyakran használt modellmentes RL algoritmus. Feltárási stratégiáikban különböznek, míg kihasználási stratégiáik hasonlóak. Míg a Q-learning egy off-policy módszer, amelyben az ágens a másik politikából származtatott a* akció alapján tanulja meg az értéket, addig a SARSA egy on-policy módszer, amelyben az aktuális politikából származtatott a aktuális akció alapján tanulja meg az értéket. Ez a két módszer egyszerűen megvalósítható, de hiányzik belőlük az általánosság, mivel nem képesek a nem látott állapotokra vonatkozó értékek becslésére.

Ezt fejlettebb algoritmusokkal, például a Deep Q-Networks(DQNs) algoritmusokkal lehet kiküszöbölni, amelyek neurális hálózatokat használnak a Q-értékek becslésére. A DQN-ek azonban csak diszkrét, alacsony dimenziós akciótereket tudnak kezelni.

A Deep Deterministic Policy Gradient(DDPG) egy modellmentes, politikán kívüli, szereplő-kritikus algoritmus, amely ezt a problémát úgy kezeli, hogy nagy dimenziós, folytonos akcióterekben tanul politikákat. Az alábbi ábra a szereplő-kritikus architektúra ábrázolása.

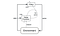
Melyek a megerősítéses tanulás gyakorlati alkalmazásai?

Mivel az RL sok adatot igényel, ezért leginkább olyan területeken alkalmazható, ahol a szimulált adatok könnyen rendelkezésre állnak, mint például a játék, robotika.

1. Az RL-t elég széles körben használják a számítógépes játékokat játszó AI építésében. Az AlphaGo Zero az első számítógépes program, amely legyőzte a világbajnokot az ősi kínai Go játékban. Mások közé tartoznak az ATARI játékok, Backgammon ,stb
2. A robotikában és az ipari automatizálásban az RL-t arra használják, hogy a robot hatékony adaptív vezérlőrendszert hozzon létre magának, amely tanul a saját tapasztalataiból és viselkedéséből. A DeepMind Deep Reinforcement Learning for Robotic Manipulation with Asynchronous Policy updates című munkája jó példa erre. Nézze meg ezt az érdekes bemutató videót.

Az RL további alkalmazásai közé tartoznak az absztrakt szövegösszefoglaló motorok, a felhasználói interakciókból tanulni képes és idővel javuló párbeszéd-ügynökök (szöveg, beszéd), az optimális kezelési irányelvek tanulása az egészségügyben és az RL-alapú ügynökök az online részvénykereskedelemben.

Hogyan kezdhetek bele a megerősítéses tanulásba?

Az RL alapfogalmainak megértéséhez a következő forrásokra támaszkodhatunk:

1. Reinforcement Learning-An Introduction, a megerősítéses tanulás atyjának, Richard Suttonnak és doktori tanácsadójának, Andrew Bartónak a könyve. A könyv online vázlata itt érhető el.
2. David Silver tananyaga, beleértve a videóelőadásokat is, egy nagyszerű bevezető kurzus az RL-ről.
3. Itt egy másik technikai bemutató az RL-ről Pieter Abbeel és John Schulman (Open AI/ Berkeley AI Research Lab) tollából.

Az RL-ügynökök építésének és tesztelésének megkezdéséhez a következő források lehetnek hasznosak.

1. Ez a blog arról, hogyan képezzünk ki egy neurális hálózati ATARI Pong-ügynököt Policy Gradients segítségével nyers pixelekből Andrej Karpathy által, segít abban, hogy az első Deep Reinforcement Learning-ügynököt mindössze 130 sor Python-kódból elkészítsük.
2. A DeepMind Lab egy nyílt forráskódú 3D-s játékszerű platform, amelyet az ágensalapú AI-kutatáshoz hoztak létre gazdag szimulált környezetekkel.
3. A Project Malmo egy másik AI-kísérleti platform az AI alapkutatás támogatására.
4. Az OpenAI gym egy eszközkészlet megerősítéses tanulási algoritmusok építésére és összehasonlítására.