 |
Egyoldalú háromszög |
|
Egy egyenlő oldalú háromszög HÁROM konstrukcióját fogjuk elkészíteni. Az első feladat egy egyenlő oldalú háromszög konstruálása lesz az egyik oldal hosszának megadásával, a másik kettő pedig egy körbe beírt egyenlő oldalú háromszög konstruálása lesz.
|
Adott: a háromszög egyik oldalának hossza
Konstruáljuk: egy egyenlő oldalú háromszöget |
 |
LÉPÉSEK:
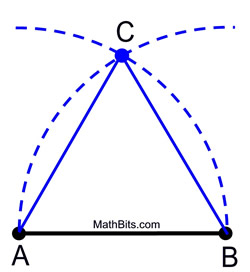
1. Helyezd az iránytűpontot az A pontra, és mérd meg a távolságot a B pontig. Lengess egy ekkora ívet a szakasz felett (vagy alatt).
2. Anélkül, hogy az iránytűn változtatnád a távolságot, helyezd az iránytűpontot a B pontra, és lengess ugyanilyen ívet, amely metszi az első ívet.
3. A metszéspontot jelöljük meg az egyenlő oldalú háromszög harmadik csúcsaként.
 |
Nézzük meg a teljes köröket munka közben.
 |
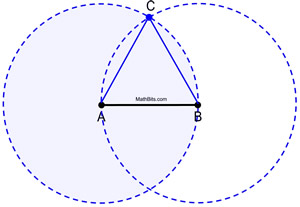A konstrukció bizonyítása: Az A kör kongruens a B körrel, mivel mindkettő azonos AB sugárhosszúsággal alakult ki. Mivel AB és AC az A kör sugarainak hossza, ezért ezek egyenlőek egymással. Hasonlóképpen, AB és BC a B kör sugarai, és egyenlőek egymással. Ezért a helyettesítés (vagy tranzitív tulajdonság) alapján AB = AC = BC. Mivel a kongruens szakaszok egyenlő hosszúságúak, 
és ΔABC egyenlő oldalú (három kongruens oldala van).
|
Adott: egy darab papír
Konstruáljuk: egy körbe írt egyenlő oldalú háromszög. |
Ez egy körbe írt szabályos hatszög konstrukciójának módosítása.
|
LÉPÉSEK:
1. Helyezd az iránytű hegyét a papírra, és rajzolj egy kört. (Tartsd meg ezt az iránytávot!)
2. Helyezz el egy A feliratú pontot a kör kerületén bárhol, hogy kiindulópontként szolgáljon.
3. Anélkül, hogy megváltoztatnád az iránytű távolságát, helyezd az iránytűpontot az A pontra, és húzz egy kis ívet, amely keresztezi a kör kerületét.
4. Anélkül, hogy megváltoztatnád az iránytű távolságát, vidd az iránytűpontot az előző ív és a kerület metszéspontjába, és készíts egy újabb kis ívet a kör kerületén.
5. Ismételjük meg ezt a “lépegetést” a kör körül, amíg vissza nem térünk az A ponthoz.
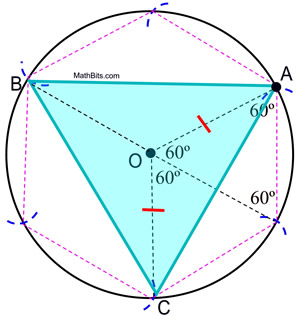
6. Az A pontból kiindulva kössük össze a kör minden további ívét, hogy egyenlő oldalú háromszöget alkossunk.
 |
A konstrukció bizonyítására vonatkozó további információkért lásd a beírt szabályos hatszög bizonyítását.
|
A konstrukció bizonyítása: A beírt szabályos hatszög bizonyítása megmutatja, hogy egy szabályos hatszög középső szögei 60º-ot tartalmaznak. A körbe beírt háromszög központi szögei 120º-ot tartalmaznak. Mivel ΔAOC egyenlő szárú (OA és OC sugárhosszúságok), m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC 
ΔCOB ΔBOA az SAS által. CPCTC szerint ∠OCB ∠OCA és m∠OCB = 30º helyettesítéssel és m∠BCA = 60º. Hasonló módon kapjuk, hogy m∠ACB = m∠CBA = m∠BAC = 60º és egyenlő oldalú ΔABC.
|
Adott: egy darab papír
Konstruáljuk: egy körbe írt egyenlő oldalú háromszöget. |
Ez a módszer a 30º – 60º – 90º speciális derékszögű háromszög ismeretét használja.
|
LÉPÉSEK:
1. Helyezd az iránytű pontját a papírra, és rajzolj egy kört, O-t. (Tartsd meg ezt az iránytávot!)
2. Egy egyenes vonalzóval rajzold meg a kör átmérőjét, jelölve a végpontokat P és B.
3. Az iránytű átmérőjének megváltoztatása nélkül helyezd az iránytű pontját P-re, és rajzolj egy teljes kört.
4. A két kör kerületének metszéspontjait jelöld meg A-val és C-vel.
5. A két kör kerületének metszéspontjait jelöld meg A-val és C-vel. Rajzoljunk szakaszokat A-tól B-ig, B-től C-ig és C-től A-ig, hogy egyenlő oldalú háromszöget alkossunk.
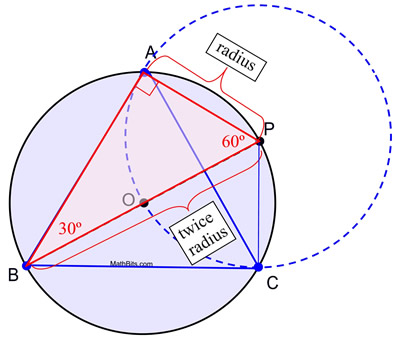
A konstrukció bizonyítása: Ez a konstrukció felhasználja azt a tényt, hogy a félkörbe beírt szög derékszög, és hogy a 30º-60º-90º háromszögben a rövid láb hossza a hipotenzus hosszának fele. Ebben a konstrukcióban az O és a P kör kongruens, mivel azonos sugarúak. Az AP a P kör sugárhossza és az AP = OP sugarak. OP szintén az O kör sugárhossza (OB-val együtt) és átmérője BP = BO + OP = 2 OP. Helyettesítéssel BP = 2 AP, ami megteremti a m∠ABP = 30º-hoz szükséges feltételeket. Következésképpen m∠APB = 60º. Hasonló érveléssel megállapítható, hogy ΔPBC esetében m∠PBC = 30º és m∠BPC = 60º, így ΔPBC ΔPBA az ASA által (B-től P-ig közös oldallal).
Most, 
mivel ezek a két egybeeső háromszög megfelelő oldalai, így ΔABC egyenlő szárú. ∠BAC ∠BCA, mivel az egyenlő szárú háromszög alapszögei kongruensek.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º a szögösszeadási posztulátum és a helyettesítés alapján. m∠BAC + m∠BCA + m∠ABC = 180º, mert a háromszög szögmértékeinek összege 180º. Mivel m∠BAC + m∠BAC + 60º = 180º helyettesítéssel tudjuk, hogy 2m∠BAC = 120º és m∠BAC = 60º. Következésképpen m∠BCA a behelyettesítéssel szintén 60º, így ΔABC egyenlő oldalú lesz.
