Beginner's Guide to Feature Selection in Python

Ha többet szeretnél tanulni Pythonban, vedd fel a DataCamp ingyenes Intro to Python for Data Science kurzusát.

Mindannyian láttatok már adathalmazokat. Néha kicsik, de gyakran időnként iszonyatosan nagy méretűek. Nagy kihívássá válik az olyan adatkészletek feldolgozása, amelyek nagyon nagyok, legalábbis elég jelentősek ahhoz, hogy feldolgozási szűk keresztmetszetet okozzanak.

Szóval, mitől ilyen nagyok ezek az adatkészletek? Nos, a jellemzők miatt. Minél több a jellemzők száma, annál nagyobbak lesznek az adatkészletek. Nos, nem mindig. Találsz olyan adathalmazokat, ahol a jellemzők száma nagyon sok, de nem tartalmaznak ennyi példányt. De itt most nem erről van szó. Szóval, egy commodity számítógéppel a kezünkben elgondolkodhatunk azon, hogyan lehet az ilyen típusú adatkészleteket feldolgozni anélkül, hogy a bokorba vernénk őket.

Gyakran előfordul, hogy egy nagy dimenziójú adatkészletben marad néhány teljesen irreleváns, jelentéktelen és érdektelen jellemző. Megfigyelték, hogy az ilyen típusú jellemzők hozzájárulása gyakran kisebb a prediktív modellezéshez, mint a kritikus jellemzőké. Előfordulhat, hogy a hozzájárulásuk nulla. Ezek a jellemzők számos problémát okoznak, ami viszont megakadályozza a hatékony prediktív modellezés folyamatát –

• Szükségtelen erőforrás-allokáció ezekre a jellemzőkre.
• Ezek a jellemzők zajként viselkednek, amelyek miatt a gépi tanulási modell borzasztóan rosszul teljesíthet.
• A gépi modell betanítása több időt vesz igénybe.

Szóval, mi itt a megoldás? A leggazdaságosabb megoldás a Feature Selection.

A Feature Selection az a folyamat, amelynek során egy adott adathalmazból kiválasztjuk a legjelentősebb jellemzőket. A Feature Selection sok esetben javíthatja a gépi tanulási modell teljesítményét is.

Erdekesnek hangzik, ugye?

Egy informális bevezetést kaptál a Feature Selectionről és annak fontosságáról az adattudomány és a gépi tanulás világában. Ebben a bejegyzésben a következőkkel fogsz foglalkozni:

• A feature selection bevezetése és fontosságának megértése
• A feature selection és a dimenzionalitáscsökkentés közötti különbség
• A feature selection módszerek különböző típusai
• A különböző feature selection módszerek implementálása a scikit-rel
• .learn

Elvezetés a jellemzőválasztásba

A jellemzőválasztás változóválasztásként vagy attribútumválasztásként is ismert.

Lényegében a legfontosabbak/relevánsak kiválasztásának folyamata. Jellemzők kiválasztása egy adathalmazból.

A jellemzőkiválasztás fontosságának megértése

A jellemzőkiválasztás fontosságát akkor ismerhetjük fel a legjobban, ha olyan adathalmazzal van dolgunk, amely hatalmas számú jellemzőt tartalmaz. Az ilyen típusú adathalmazt gyakran nevezik nagy dimenziójú adathalmaznak. Nos, ezzel a nagy dimenzionalitással rengeteg probléma jár, például – ez a nagy dimenzionalitás jelentősen megnöveli a gépi tanulás modelljének képzési idejét, nagyon bonyolulttá teheti a modellt, ami viszont túlillesztéshez vezethet.

A nagy dimenziós jellemzőhalmazban gyakran marad számos olyan jellemző, amely redundáns, vagyis ezek a jellemzők nem mások, mint a többi lényeges jellemző kiterjesztései. Ezek a redundáns jellemzők nem járulnak hozzá hatékonyan a modellképzéshez sem. Tehát nyilvánvalóan szükség van az adathalmaz legfontosabb és legrelevánsabb jellemzőinek kinyerésére annak érdekében, hogy a leghatékonyabb prediktív modellezési teljesítményt érjük el.”

“A változóválasztás célja hármas: a prediktorok előrejelzési teljesítményének javítása, gyorsabb és költséghatékonyabb prediktorok biztosítása, valamint az adatokat generáló mögöttes folyamat jobb megértése.”

Egy bevezetés a változó- és jellemzőkiválasztásba

Most értsük meg a különbséget a dimenziócsökkentés és a jellemzőkiválasztás között.

Néha a jellemzőkiválasztást összetévesztik a dimenziócsökkentéssel. De ezek különböznek egymástól. A feature selection különbözik a dimenzionalitáscsökkentéstől. Mindkét módszer az adathalmazban lévő attribútumok számának csökkentésére törekszik, de a dimenziócsökkentő módszer ezt az attribútumok új kombinációinak létrehozásával teszi (ezt néha feature-transzformációnak nevezik), míg a feature-szelekciós módszerek az adatokban meglévő attribútumokat tartalmazzák és kizárják anélkül, hogy megváltoztatnák azokat.

A dimenzionalitáscsökkentő módszerek néhány példája a főkomponens-elemzés, a szinguláris érték dekompozíció, a lineáris diszkriminancia-elemzés stb.

Hadd foglaljam össze önnek a jellemzőválasztás fontosságát:

• Ez lehetővé teszi a gépi tanulási algoritmus gyorsabb betanítását.
• csökkenti a modell komplexitását és könnyebben értelmezhetővé teszi azt.
• javítja a modell pontosságát, ha a megfelelő részhalmazt választjuk ki.
• csökkenti a túlillesztést.

A következő részben az általános jellemzőkiválasztási módszerek különböző típusait tanulmányozza: a szűrőmódszereket, a burkolómódszereket és a beágyazott módszereket.

Szűrőmódszerek

A következő kép jellemzi legjobban a szűrőalapú jellemzőkiválasztási módszereket:

A kép forrása: Forrás: Analytics Vidhya

A szűrő módszer a kiértékelendő adatok általános egyediségére és a feature részhalmaz kiválasztására támaszkodik, nem tartalmaz semmilyen bányászati algoritmust. A szűrő módszer a pontos értékelési kritériumot használja, amely magában foglalja a távolságot, az információt, a függőséget és a konzisztenciát. A szűrő módszer a rangsorolási technika fő kritériumait használja, és a változó kiválasztásához a rangsorolási módszert alkalmazza. A rangsorolási módszer használatának oka az egyszerűség, kiváló és releváns jellemzők előállítása. A rangsorolási módszer az osztályozási folyamat megkezdése előtt kiszűri a nem releváns jellemzőket.

A szűrő módszereket általában az adatok előfeldolgozási lépéseként használják. A jellemzők kiválasztása független bármely gépi tanulási algoritmustól. A jellemzők statisztikai pontszámok alapján adnak rangsort, amelyek általában meghatározzák a jellemzők korrelációját a kimeneti változóval. A korreláció erősen kontextusfüggő fogalom, és munkáról munkára változik. A különböző típusú (jelen esetben folytonos és kategorikus) adatokra vonatkozó korrelációs együtthatók meghatározásához a következő táblázatot használhatja.

Kép forrása: Analytics Vidhya

Az egyes szűrőmódszerek közül néhány példa a Chi-négyzet teszt, az információnyereség és a korrelációs együttható pontszámok.

A következőkben a Wrapper-módszerek következnek.

Wrapper módszerek

A szűrő módszerekhez hasonlóan hadd adjak egy ugyanilyen infógrafikát, amely segít jobban megérteni a wrapper módszereket:

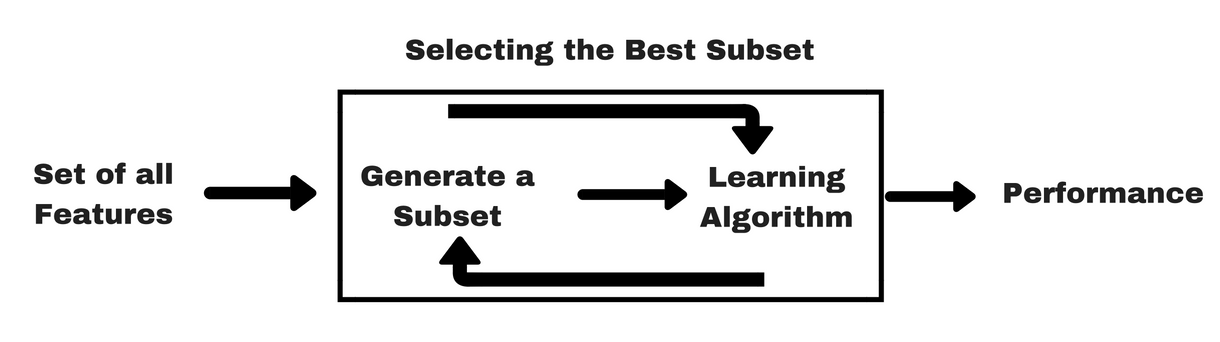
Kép forrása: Analytics Vidhya

Amint a fenti képen látható, egy wrapper-módszerhez egy gépi tanulási algoritmusra van szükség, és annak teljesítményét használja értékelési kritériumként. Ez a módszer olyan jellemzőt keres, amely a legjobban illeszkedik a gépi tanulási algoritmushoz, és célja a bányászati teljesítmény javítása. A jellemzők értékeléséhez az osztályozási feladatokhoz használt előrejelzési pontosságot és a klaszterek jóságát klaszterezéssel értékelik.

A wrapper módszerek néhány tipikus példája a forward feature selection, backward feature elimination, recursive feature elimination stb.

• Forward Selection: Az eljárás a jellemzők üres halmazával kezdődik . Az eredeti jellemzők közül a legjobbat határozzuk meg, és hozzáadjuk a redukált halmazhoz. Minden következő iterációnál a megmaradt eredeti jellemzők közül a legjobbat adjuk hozzá a halmazhoz.
• Visszafelé történő kiküszöbölés: Az eljárás az attribútumok teljes halmazával kezdődik. Minden egyes lépésben eltávolítja a halmazban maradó legrosszabb attribútumot.
• Az előremenő kiválasztás és a visszafelé történő eliminálás kombinációja: A lépésenkénti előremenő kiválasztás és a visszafelé történő elimináció kombinálható úgy, hogy az eljárás minden egyes lépésben kiválasztja a legjobb attribútumot, és eltávolítja a legrosszabbat a maradék attribútumok közül.
• Rekurzív jellemző-elimináció: A rekurzív jellemzőelimináció mohó keresést végez a legjobban teljesítő jellemző részhalmaz megtalálására. Iteratív módon hoz létre modelleket, és minden egyes iterációnál meghatározza a legjobb vagy a legrosszabb teljesítményű jellemzőt. A következő modelleket a meghagyott jellemzőkkel építi fel, amíg az összes jellemzőt fel nem tárja. Ezután rangsorolja a jellemzőket a kiküszöbölésük sorrendje alapján. A legrosszabb esetben, ha egy adathalmaz N számú jellemzőt tartalmaz, az RFE mohó keresést végez a jellemzők 2N kombinációjára.

Elég jó!

Most tanulmányozzuk a beágyazott módszereket.

Beágyazott módszerek

A beágyazott módszerek iteratívak abban az értelemben, hogy a modellképzési folyamat minden egyes iterációjára ügyel, és gondosan kivonja azokat a jellemzőket, amelyek a leginkább hozzájárulnak az adott iteráció képzéséhez. A regularizációs módszerek a leggyakrabban használt beágyazott módszerek, amelyek büntetik a jellemzőt egy együttható küszöbértékének megadásával.

Ezért a regularizációs módszereket büntetési módszereknek is nevezik, amelyek egy prediktív algoritmus (például egy regressziós algoritmus) optimalizálásába olyan további megkötéseket vezetnek be, amelyek a modellt az alacsonyabb komplexitás (kevesebb együttható) felé terelik.

Példák a regularizációs algoritmusokra a LASSO, az Elastic Net, a Ridge Regression stb.

A szűrő- és wrapper-módszerek közötti különbség

Hát, időnként zavaró lehet a szűrő- és wrapper-módszerek közötti különbségtétel a funkcionalitásukat tekintve. Nézzük meg, hogy milyen pontokon különböznek egymástól.

• A szűrő módszerek nem tartalmaznak gépi tanulási modellt annak meghatározásához, hogy egy jellemző jó vagy rossz, míg a wrapper módszerek gépi tanulási modellt használnak, és betanítják a jellemzőt annak eldöntéséhez, hogy az lényeges-e vagy sem.
• A szűrő módszerek sokkal gyorsabbak a wrapper módszerekhez képest, mivel nem igénylik a modellek betanítását. Másrészt a wrapper módszerek számításigényesek, és hatalmas adathalmazok esetén a wrapper módszerek nem a leghatékonyabb figyelembe vehető jellemzőválasztási módszer.
• A szűrő módszerek esetleg nem találják meg a jellemzők legjobb részhalmazát olyan helyzetekben, amikor nincs elég adat a jellemzők statisztikai korrelációjának modellezéséhez, de a wrapper módszerek kimerítő jellegük miatt mindig képesek a jellemzők legjobb részhalmazát megadni.
• A wrapper módszerekből származó jellemzők használata a végső gépi tanulási modellben túlillesztéshez vezethet, mivel a wrapper módszerek már gépi tanulási modelleket képeznek a jellemzőkkel, és ez befolyásolja a tanulás valódi teljesítményét. A szűrőmódszerekből származó jellemzők azonban az esetek többségében nem vezetnek túlillesztéshez

Az eddigiekben tanulmányoztad a jellemzők kiválasztásának fontosságát, megértetted a különbségét a dimenziócsökkentéssel. A különböző típusú jellemzőkiválasztási módszerekkel is foglalkoztál. Eddig minden rendben!

Most lássunk néhány csapdát, amibe beleeshetsz a feature selection végrehajtása során:

Fontos megfontolás

Már megérthetted, hogy a feature selection mit ér egy gépi tanulási pipeline-ban, és milyen szolgáltatásokat nyújt, ha integráljuk. Nagyon fontos azonban megérteni, hogy pontosan hol kell integrálnia a jellemzőválasztást a gépi tanulási csővezetékébe.

Egyszerűen szólva, a jellemzőválasztási lépést be kell építenie, mielőtt az adatokat betáplálná a modellbe képzés céljából, különösen akkor, ha olyan pontosságbecslési módszereket használ, mint a kereszt-validálás. Ez biztosítja, hogy a jellemzőkiválasztás közvetlenül a modell betanítása előtt kerüljön végrehajtásra az adathalmazon. Ha azonban először elvégzi a jellemzőválasztást az adatok előkészítése érdekében, majd a kiválasztott jellemzőkön végzi a modellválasztást és a képzést, akkor ez hiba lenne.

Ha a jellemzőválasztást az összes adaton elvégzi, majd kereszt-validál, akkor a kereszt-validálási eljárás minden egyes foldjában a tesztadatokat is felhasználták a jellemzők kiválasztásához, és ez hajlamos torzítani a gépi tanulás modelljének teljesítményét.

Elég az elméletekből! Térjünk most rögtön a kódolásra.

Egy esettanulmány Pythonban

Ezért az esettanulmányért a Pima Indians Diabetes adathalmazt fogjuk használni. Az adathalmaz leírása itt található.

Az adathalmaz osztályozási feladatnak felel meg, amelyen 8 jellemző alapján kell megjósolni, hogy egy személy cukorbeteg-e.

Az adathalmazban összesen 768 megfigyelés van. Az első feladata az adathalmaz betöltése, hogy folytatni tudja a munkát. De előtte importáljuk be a szükséges függőségeket, amelyekre szükséged lesz. A többit menet közben importálhatja.

import pandas as pdimport numpy as np

Most, hogy a függőségek importálva vannak, töltsük be a Pima Indiánok adathalmazát egy Dataframe objektumba a Pandas könyvtár segítségével.

data = pd.read_csv("diabetes.csv")

Az adathalmaz sikeresen betöltődött a Dataframe objektum adataiba. Most nézzük meg az adatokat.

data.head()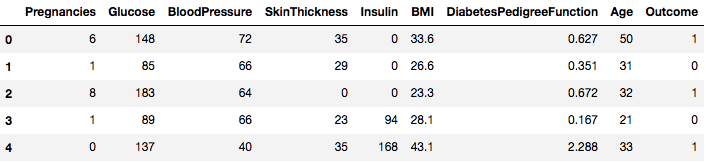

Így láthatjuk, hogy 8 különböző jellemzőt címkézünk fel 1 és 0 kimenetellel, ahol az 1 azt jelenti, hogy a megfigyelés cukorbeteg, a 0 pedig azt, hogy a megfigyelés nem cukorbeteg. Az adathalmazról ismert, hogy hiányzó értékeket tartalmaz. Konkrétan néhány oszlop esetében hiányoznak olyan megfigyelések, amelyek nulla értékként vannak jelölve. Erre az említett oszlopok definíciójából lehet következtetni, és nem praktikus, hogy a nulla érték érvénytelen ezekre az intézkedésekre, például, a testtömegindex vagy a vérnyomás esetében a nulla érték érvénytelen.

De ehhez a bemutatóhoz közvetlenül az adatállomány előfeldolgozott változatát fogja használni.

# load dataurl = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv"names = dataframe = pd.read_csv(url, names=names)

Az adatokat most egy dataframe nevű DataFrame objektumba töltötte be.

A gyorsabb számítás elérése érdekében alakítsuk át a DataFrame objektumot NumPy tömbgé. Emellett különítsük el az adatokat külön változókba, hogy a jellemzők és a címkék elkülönüljenek egymástól.

array = dataframe.valuesX = arrayY = array

Nagyszerű! Előkészítetted az adataidat.

Először egy Chi-Squared statisztikai tesztet fogsz végrehajtani nem negatív jellemzők esetén, hogy kiválaszd a 4 legjobb jellemzőt az adathalmazból. Már láttad, hogy a Chi-Squared teszt a szűrőmódszerek osztályába tartozik. Ha valaki kíváncsi a Chi-Squared belsejének megismerésére, ez a videó kiváló munkát végez.

A scikit-learn könyvtár biztosítja a SelectKBest osztályt, amely egy sor különböző statisztikai teszttel használható egy adott számú jellemző kiválasztására, ebben az esetben ez a Chi-Squared.

# Import the necessary libraries firstfrom sklearn.feature_selection import SelectKBestfrom sklearn.feature_selection import chi2

A kísérletek futtatásához importáltad a könyvtárakat. Most nézzük meg működés közben.

# Feature extractiontest = SelectKBest(score_func=chi2, k=4)fit = test.fit(X, Y)# Summarize scoresnp.set_printoptions(precision=3)print(fit.scores_)features = fit.transform(X)# Summarize selected featuresprint(features)

 ]

Interpretáció:

Láthatja az egyes attribútumok pontszámát és a kiválasztott 4 attribútumot (a legmagasabb pontszámmal rendelkezőket): plas, teszt, tömeg és kor. Ezek a pontszámok tovább segítenek a legjobb jellemzők meghatározásában a modell képzéséhez.

M.S.: Az első sor a jellemzők nevét jelöli. Az adathalmaz előfeldolgozásához a neveket numerikusan kódoltuk.

A következő lépésben a Recursive Feature Elimination-t (rekurzív jellemző-elimináció) fogja megvalósítani, amely egyfajta wrapper jellemző-kiválasztási módszer.

A Recursive Feature Elimination (vagy RFE) úgy működik, hogy rekurzívan eltávolítja az attribútumokat, és a megmaradó attribútumokra építi a modellt.

A modell pontosságát használja arra, hogy azonosítsa, mely attribútumok (és attribútumok kombinációja) járulnak hozzá leginkább a célattribútum előrejelzéséhez.

A scikit-learn dokumentációjában többet megtudhat a RFE osztályról.

# Import your necessary dependenciesfrom sklearn.feature_selection import RFEfrom sklearn.linear_model import LogisticRegression

Az RFE-t a Logistic Regression osztályozóval együtt fogja használni a 3 legjobb jellemző kiválasztásához. Az algoritmus kiválasztása nem számít túl sokat, amíg ügyes és konzisztens.

# Feature extractionmodel = LogisticRegression()rfe = RFE(model, 3)fit = rfe.fit(X, Y)print("Num Features: %s" % (fit.n_features_))print("Selected Features: %s" % (fit.support_))print("Feature Ranking: %s" % (fit.ranking_))

Num Features: 3Selected Features: Feature Ranking: 

Láthatjuk, hogy az RFE kiválasztotta a 3 legjobb jellemzőt: preg, mass és pedi.

Ezeket a support tömbben True értékkel, a ranking tömbben pedig “1” választással jelöljük. Ez viszont ezeknek a jellemzőknek az erősségét jelzi.

A következőkben a Ridge-regressziót fogjuk használni, ami alapvetően egy regularizációs technika és egy beágyazott jellemzőválasztási technika is.

Ez a cikk kiváló magyarázatot ad a Ridge-regresszióról. Mindenképpen nézd meg.

# First things firstfrom sklearn.linear_model import Ridge

A következő lépésben a Ridge regressziót fogod használni az R2 együttható meghatározására.

Még a scikit-learn hivatalos dokumentációját fogod megnézni a Ridge regresszióról.

ridge = Ridge(alpha=1.0)ridge.fit(X,Y)

Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None, normalize=False, random_state=None, solver='auto', tol=0.001)

A Ridge regresszió eredményeinek jobb megértése érdekében egy kis segédfüggvényt fogsz implementálni, amely segít neked az eredményeket jobban kiírni, hogy könnyen értelmezni tudd őket.

# A helper method for pretty-printing the coefficientsdef pretty_print_coefs(coefs, names = None, sort = False): if names == None: names = lst = zip(coefs, names) if sort: lst = sorted(lst, key = lambda x:-np.abs(x)) return " + ".join("%s * %s" % (round(coef, 3), name) for coef, name in lst)

A következőkben átadja a Ridge-modell együtthatóterminusait ennek a kis függvénynek, és megnézi, mi történik.

print ("Ridge model:", pretty_print_coefs(ridge.coef_))

Ridge model: 0.021 * X0 + 0.006 * X1 + -0.002 * X2 + 0.0 * X3 + -0.0 * X4 + 0.013 * X5 + 0.145 * X6 + 0.003 * X7

A feature-változókhoz csatolt összes együtthatótermit észreveheti. Ez ismét segíteni fog a leglényegesebb jellemzők kiválasztásában. Az alábbiakban néhány pontot érdemes szem előtt tartani a Ridge-regresszió alkalmazása során:

• L2-regularizációnak is nevezik.
• A korrelált jellemzők esetében ez azt jelenti, hogy hajlamosak hasonló együtthatókat kapni.
• A negatív együtthatókkal rendelkező jellemzők nem járulnak hozzá olyan sokat. De egy összetettebb forgatókönyvben, ahol rengeteg jellemzővel van dolgunk, akkor ez a pontszám mindenképpen segít a végső jellemzőválasztási döntéshozatali folyamatban.

Nos, ezzel az esettanulmányi rész végére értünk. A fenti szakaszban megvalósított módszerek segítenek egy adott adatkészlet jellemzőinek átfogó megértésében. Hadd mondjak néhány kritikus pontot ezekről a technikákról:

• A jellemzők kiválasztása alapvetően az adatok előfeldolgozásának része, amelyet minden gépi tanulási csővezeték legidőigényesebb részének tartanak.
• Ezek a technikák segítenek abban, hogy szisztematikusabban és gépi tanulásbarát módon közelítsen hozzá. Képes leszel pontosabban értelmezni a jellemzőket.

Pakolás!

Ebben a bejegyzésben az egyik legjobban tanulmányozott és kutatott statisztikai témát, azaz a jellemzők kiválasztását tárgyaltad. Megismerkedtél annak különböző változataival is, és felhasználtad őket arra, hogy megnézd, mely jellemzők fontosak egy adathalmazban.

Ezt a bemutatót tovább folytathatod azzal, hogy egy korrelációs mértéket beolvasztasz a wrapper módszerbe, és megnézed, hogyan teljesít. A művelet során lehet, hogy végül saját feature-kiválasztási mechanizmust hoz létre. Így megalapozhatod a kis kutatásodat. A kutatók különböző soft computing elveket is alkalmaznak a kiválasztás elvégzéséhez. Ez önmagában egy egész tanulmány- és kutatási terület. Emellett ki kell próbálnod a meglévő jellemző-kiválasztási algoritmusokat különböző adathalmazokon, és le kell vonnod a saját következtetéseidet.

Miért vannak még mindig érvényben ezek a hagyományos jellemző-kiválasztási módszerek?

Igen, ez a kérdés nyilvánvaló. Mert léteznek olyan neurális háló architektúrák (például CNN-ek), amelyek igenis képesek a legjelentősebb jellemzők kinyerésére az adatokból, de ennek is van egy korlátja. Egy CNN használata egy olyan rendszeres táblázatos adathalmazhoz, amely nem rendelkezik speciális tulajdonságokkal (azokkal a tulajdonságokkal, amelyeket egy tipikus kép tartalmaz, mint például az átmeneti tulajdonságok, élek, pozíciós tulajdonságok, kontúrok stb.), nem a legbölcsebb döntés. Ráadásul, ha korlátozott adatokkal és korlátozott erőforrásokkal rendelkezik, a CNN rendszeres táblázatos adatkészleteken történő képzése teljes pazarlássá válhat. Ilyen helyzetekben tehát mindenképpen jól jönnek a tanult módszerek.

Az alábbi forrásokból válogathat, ha szeretne még többet ásni a témában:

• Feature Selection for Knowledge Discovery and Data Mining
• Subspace, Latent Structure, and Feature Selection: Statistical and Optimization Perspectives Workshop
• Feature Selection: Problem statement and Uses
• Using genetic algorithms for feature selection in Data Analytics

Az alábbiakban találhatók azok a hivatkozások, amelyeket ennek az útmutatónak a megírásához felhasználtunk.

• Data Mining: Jiawei Han Micheline Kamber Jian Pei.
• Egy bevezetés a feature selectionbe
• Analytics Vidhya cikk a feature selectionről
• Hierarchical and Mixed Model – DataCamp kurzus
• Feature Selection For Machine Learning in Python
• Outlier Detection in Stream Data by MachineLearning and Feature Selection Methods
• S. Visalakshi és V. Radha, “A feature selection technikák és alkalmazások irodalmi áttekintése: Review of feature selection in data mining,” 2014 IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, 2014, pp. 1-6.