Mielőtt elkezdenénk, meg kell tennünk néhány feltevést.
Először is, newtoni folyadékokkal dolgozunk. Ez a legegyszerűbb matematikai módja annak, hogy egy folyadék viszkozitását figyelembe vegyük. Nincsenek olyan valós folyadékok, amelyek tökéletesen ebbe a kategóriába esnek, de a legtöbb esetben a levegő és a víz Newton-féle folyadékként kezelhető. A másik nagyon fontos feltevésünk, hogy a folyadék összenyomhatatlan. Ez azt jelenti, hogy sűrűsége, rho, állandó.
Tömegmegmaradás
Az első egyenlet azt mondja, hogy a folyadék tömege, amellyel dolgozunk, megmarad. A folyadék megváltoztathatja az alakját, de ez az egyenlet azt mondja, hogy a tömege az elejétől a végéig ugyanaz.
Most beszéljünk a matematikáról. Az u betű a folyadék sebességét jelöli, és ez egy vektor. Három összetevője van, ezeket u, v, w-nek nevezhetjük, és ezek a folyadék sebességét jelentik x, y és z irányban. A görög nabla ∇ betű, amelyet egy pont követ, a divergenciaoperátor. Ez azt jelenti, hogy minden irányban (jelen esetben x, y, z) differenciálnunk kell az összetevőit.

Az első derivált megmondja, hogyan változik a sebesség x komponense, miközben az x irányban mozgunk. Ugyanez igaz a másik két deriváltra is. Mivel ez az egyenlet egyenlő nullával, megmutatja nekünk, hogy a tömeg megmarad.
A lendület megőrzése

A második egyenlet valójában három differenciálegyenletből áll. Ez az, amely a folyadékokra Newton második törvényeként írható le. Ha a kifejezést kibővítjük, egy összetett rendszert kapunk.
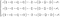
Mivel ez sokkal egyszerűbben érthető, ezért most a nem kiterjesztett lendületmegőrzésre fogunk koncentrálni.
Ha folyadékokkal dolgozunk, akkor azt mondhatjuk, hogy a tömeg és a sűrűség ugyanaz a dolog (amíg a térfogatuk azonos). Ha két folyadékot vizsgálunk, akkor azt mondhatjuk, hogy a sűrűbb a “nehezebb” (pl. higany és víz). Ebben az esetben a görög ρ (rho) betű a folyadék sűrűsége.
A tömeg megvan, most, hogy visszatérjünk Newton második törvényéhez, szükségünk van a gyorsulásra. Ez pontosan a sebességvektor időbeli deriváltjának eredménye.

Most már csak az egyenlőségjel jobb oldalán lévő tagok maradtak, és ezek a folyadékra ható összes erőt jelentik.
Az első kifejezés ∇p a nyomás gradiense. Ez a nyomáskülönbséget jelenti abban a térben, ahol a folyadék található. Például, ha van egy alacsony nyomású és egy másik, magasabb nyomású zóna, a folyadék a magas nyomású részből az alacsonyabb nyomású felé fog mozogni. A p gradiens mondja ki mindezt.
A második kifejezés a folyadék viszkozitását írja le. Gondoljunk két különböző folyadékra, például vízre és mézre. Amikor egy pohár vizet töltesz, az gyorsan és könnyen leesik. Amikor ugyanezt megteszed a mézzel, az ragadós, és nagyon lassan ömlik. Ezt mondja ki ez a kifejezés.
Az utolsó kifejezés, az F, a legegyszerűbb, mert ez képviseli az összes külső erőt, ami az adott folyadékra hathat. Általában az erő, amit itt figyelembe veszünk, a gravitáció.
Ez az, amit az összes ilyen díszes szimbólum és betű jelent, egyszerűen erő = tömeg x gyorsulás.
A Navier-Stokes-egyenletek használata
Mivel ezeknek az egyenleteknek a megoldása olyan bonyolult, hogy használatukhoz sok közelítést kell tennünk. Néhány példa erre a Poiseuille- és a Couette-áramlás. Ez a két tudós rengeteg feltételezéssel képes volt megtalálni a Navier-Stokes-egyenletek megoldását egy nagyon speciális alkalmazáshoz. Ha azonban egy bonyolultabb feladatra, például az időjárás-előrejelzésre szeretnénk használni őket, akkor valami mást kell tennünk.
Az egyenletek használatának leggyakoribb módja az átalakításuk, a Reynolds-átlaggal. Ez egy fejlett matematikai eljárás, és az eredmény a Reynolds-egyenletek. Ezeket általában RANS (azaz Reynolds átlagolt Navier-Stokes-egyenleteknek) nevezik.
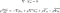
Ezeket az egyenleteket akkor használjuk, ha a folyadék turbulens áramlásban van. Majdnem pontosan úgy néznek ki, mint a Navier-Stokes-egyenletek, kivéve az utolsó tagot. Ezt Reynolds-feszültségtenzornak nevezzük. Ez az a mennyiség, amely lehetővé teszi számunkra, hogy figyelembe vegyük a folyadék turbulenciáját.
A RANS-egyenletekben az általunk használt mennyiségeket egy időintervallumon átlagoljuk. Ennek az intervallumnak elég kicsinek kell lennie ahhoz, hogy lehetővé tegye az általunk vizsgált jelenség megfigyelését. Ugyanakkor elég nagynak kell lennie ahhoz, hogy a turbulencia hatása elveszítse jelentőségét.
A megfelelő feltételezések mellett ezek az egyenletek működnek. Tudjuk, hogyan használhatjuk őket, hogy gyorsabbá tegyük az F1-es autókat, hogy egy űrhajót eljuttassunk az ISS-re, és hogy elkészítsük az időjárás-előrejelzést. Ezért talán elgondolkodik azon, hogy miért ér egymillió dollárt ezeknek az egyenleteknek a bizonyítása?
Millió dolláros díj
Fizikai szempontból ezek az egyenletek nem mások, mint Newton második törvénye, amely folyadékokkal működik. Ha teszünk néhány feltevést és egyszerűsítést, elképesztő dolgokat tudunk velük csinálni.
Az igazi probléma a következő. Ezeknek az egyenleteknek a megoldása közelítések nélkül egyszerűen borzasztóan bonyolult. Annyira bonyolult, hogy még az sem bizonyított, hogy a megoldások valóban léteznek. És itt jön a képbe a Millennium-díj.
A feladat hivatalos megfogalmazása (itt található) a következő:
Bizonyítsuk be vagy adjunk ellenpéldát a következő állításra: három térbeli dimenzióban és időben, adott kezdeti sebességmező mellett létezik olyan vektorsebesség és skalárnyomás mező, amelyek simák és globálisan meghatározottak, és amelyek megoldják a Navier-Stokes egyenleteket.
Ez azt jelenti, hogy a díj elnyeréséhez három dolgot kell tennünk:
- Bizonyítsuk be, hogy létezik megoldás
- A megoldásnak a tér minden pontján léteznie kell
- A megoldásnak simának kell lennie. Ez azt jelenti, hogy a kezdeti feltételek kis változása csak kis eltérést eredményez az eredményben.
Egy mérnök számára általában elég tudni, hogy ezek az egyenletek működnek, még ha csak valamilyen közelítéssel is. Egy matematikus számára azonban nagyon fontos tudni, hogy léteznek-e a megoldások, és hogyan viselkednek.
Most talán azt gondolja, hogy ha úgy működnek, ahogy működnek, akkor a bizonyítás keresésére fordított idő és energia teljes időpocsékolás. Nos, mint az emberiség történelmének számos technológiai vívmánya, az eredmény sem tűnhet túl fontosnak. Ami fontos, az az odavezető út, ami új ismereteket és fejlesztéseket hozhat az életünkbe.
Gondoljunk csak az űrmissziókra. Ha az emberek soha nem döntenek úgy, hogy elmennek és járnak a Holdon, akkor nem lenne sok olyan tárgyunk, amely az életünk javítására szolgál. Az MRI-készülékek és a pacemakerek az űrkutatáshoz kifejlesztett technológiákból származnak. Ma az orvosok a világ minden táján nap mint nap használják őket, hogy életeket mentsenek. Ugyanez vonatkozik itt is. A Navier-Stokes-egyenletek megoldásának felfedezéséhez vezető út segít abban, hogy jobban megértsük a folyadékokat és még sok mást is. Új felfedezésekhez vezethet minket, és valószínűleg új matematikát kell majd feltalálnunk. Ezt aztán felhasználhatjuk sok más probléma megválaszolására, új technológiák feltalálására, amelyek javítják az életünket és jobbá tesznek minket.