Ha szeretsz inni, akkor a Klein-palack nem ajánlott edény. Lehet, hogy halványan úgy néz ki, mint egy palack, de nem tartalmaz térfogatot, ami azt jelenti, hogy valójában nem tud folyadékot tartani. Bármit is öntesz “bele”, az csak újra ki fog jönni.
Hogyan építesz meg egy ilyen furcsa dolgot, és miért akarod megépíteni? Felix Klein matematikus, aki 1882-ben felfedezte a palackot, úgy írta le, mint egy olyan felületet, amelyet “úgy lehet megjeleníteni, hogy egy gumicső egy darabját megfordítjuk, és úgy engedjük át önmagán, hogy a külső és a belső találkozzon”.
Your browser does not support the video tag.Direct link
Az nyilvánvaló, hogy a Klein-palack, akárcsak az ismertebb gömb, egy zárt felület: véges abban az értelemben, hogy a tér egy véges régiójában elfér, de egy hangya a végtelenségig sétálhatna rajta anélkül, hogy valaha is találkozna egy határral vagy átesne egy peremén. A gömbbel ellentétben, amelynek van egy belső és egy külső oldala, a Klein-palack egyoldalú: a hangyánk körbesétálva a felület minden egyes pontjának mindkét oldalát elérheti. Ez az oka annak, hogy a palack nem zár be térfogatot, és ez egyben választ ad a “miért” kérdésre is: a Klein-palack azért érdekes, mert a természetben nem sok egyoldalú alakzattal találkozunk. (Egy másik nagyon szép képet a Klein-palackról lásd itt.)

A Möbius-szalag egyoldalú – nézd meg az animált változatot. (A kép és az animáció Konrad Polthier munkája.)
Ha ez egy kicsit zavaros, gondoljunk az egyoldalú felület egyszerűbb példájára: a híres Möbius-szalagra. Készíthetünk egyet, ha egy papírcsík két végét fogjuk, a csíkot megcsavarjuk, majd a végeket összeragasztjuk. Ha olyan papírcsíkot használunk, amelynek két oldala különböző színű, mondjuk zöld és narancssárga, könnyen meggyőződhetünk arról, hogy az így kapott Möbius-csík egyoldalú. Miután megcsavartuk és összeragasztottuk, rájövünk, hogy minden narancssárga pontot minden zöld pontból elérhetünk anélkül, hogy át kellene szúrnunk a papírt, vagy át kellene másznunk a szélén.
A Klein-palackkal ellentétben a Möbius-csíknak van határa – ez az eredeti csík két nem ragasztott széléből áll. De van egy kapcsolat a kettő között. Ha veszünk két Möbius-szalagot, és a határaik összekapcsolásával egy közönséges kétoldalas szalaggal zárt alakzatot hozunk létre, ahogy az alább látható, akkor pontosan a Klein-palackot kapjuk.
Az Ön böngészője nem támogatja a video tag-et.Direct link
szalag köti össze, amelynek hátsó és elülső oldala fehér, illetve kék színű. Konrad Polthier animációja.
Ez a tény Leo Moser matematikust egy limerick megírására inspirálta:
Egy Klein nevű matematikus azt gondolta, hogy a Möbius-sáv isteni.Azt mondta: “
Néhány matematikus tényleg sokoldalú tehetség!
A Klein-palack másik furcsa tulajdonsága, hogy metszi önmagát, ami azt jelenti, hogy nehéz egyetlen gumicsőből elkészíteni, ahogy Klein javasolta. Szigorúan véve a fent ábrázolt, önmagát metsző tárgy nem Klein-palack, hanem (ahogy Klein jelezte) csak annak vizualizációja. Hogy megértsük, miért, gondoljunk először az ismertebb fánkra (matematikailag tóruszként ismert). Egy négyzet alakú gumilapból úgy készíthetünk tóruszt, hogy először két ellentétes oldalát összeragasztjuk hengerré, majd a henger két határoló komponensét összeragasztjuk, így kapjuk a tóruszt.

Torusz készítése: Először ragasszunk ellentétes pontokat a négyzet két ellentétes oldalán, hogy egy hengert kapjunk, majd ragasszuk össze a henger két határoló körét (ami megfelel a négyzet fennmaradó két oldalán lévő ellentétes pontok ragasztásának), hogy egy tóruszt kapjunk.
Ha nem akarunk a ragasztással bajlódni, akkor a tóruszt egyszerűen négyzetnek tekinthetjük, szem előtt tartva, hogy az ellentétes oldalakon lévő ellentétes pontokat azonosnak tekintjük. Tehát ha a “négyzetre” rajzolt alakzatot átcsúsztatod a felső élén, akkor az újra megjelenik az alsó élén, ha pedig átcsúsztatod a jobb élén, akkor újra megjelenik a bal élén (és fordítva).
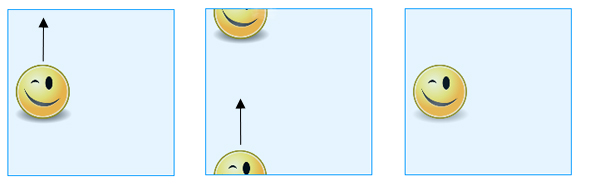
Ha a “négyzetre” rajzolt alakzatot a felső élén átcsúsztatjuk, akkor az az alsó élnél fog újra megjelenni.
Az igazi Klein-üveghez ugyanígy kezdjük, egy négyzet ellentétes oldalpárjának ellentétes pontjait azonosítva. A másik oldalpárnál azonban ne közvetlenül szemben lévő pontokat azonosítsunk, hanem átlósan szemben lévő pontokat, ahogy az a képen látható.
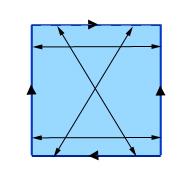
Klein palack készítése: azonosítsuk két ellentétes oldal (a képen a függőleges oldalak) ellentétes pontjait, majd azonosítsuk a maradék két oldal átlósan ellentétes pontjait. (Ha a felső és az alsó oldal pontjait balról jobbra haladva a 0-tól 1-ig terjedő számokkal jelöljük, akkor a felső oldal x jelölésű pontját azonosítjuk az alsó oldal 1-x jelölésű pontjával.)
A kapott tárgy a Klein-palack. Ismét úgy gondolhatunk rá, mint egy négyzetre, szem előtt tartva, hogy mely határpontokat tekintjük azonosnak. Ha egy olyan alakzatot csúsztatunk az egyik széle fölé, amelynek ellentétes pontjait azonosítottuk (képünkön függőlegesen), akkor az újra megjelenik újra az ellentétes oldalon, mint korábban. Ha viszont az egyik olyan él fölé csúsztatjuk, amelynek pontjait átlósan (képünkön vízszintesen) azonosították, akkor az ellenkező oldalon jelenik meg, de eltolva és eredeti önmagának tükörképeként.
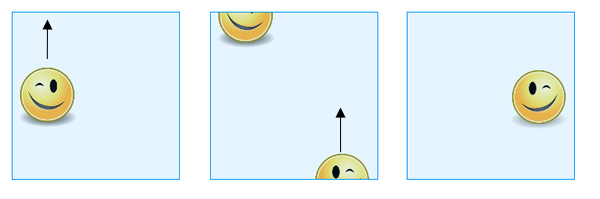
Ha a felső él fölé csúsztatjuk az alakzatot, akkor az alsó él fölött jelenik meg, de a másik oldalon, és eredeti énjének tükörképeként.
Az alakzatot csak úgy építhetjük fel a háromdimenziós térben, hogy ténylegesen pontokat ragasztunk össze, ha hagyjuk, hogy metszi önmagát. Ez annyit tesz, hogy az eredeti négyzet belsejében lévő pontpárokat azonosítjuk, így szigorúan véve az így kapott alakzat nem pontosan ugyanaz, mint a Klein-palack, amelynek csak a határpontjait azonosítjuk. Ez csak egy módja a palack ábrázolásának a háromdimenziós térben (vannak mások is).
Az Ön böngészője nem támogatja a video tag-et. közvetlen link
Tükörkép és orientálhatóság. Konrad Polthier animációja.
Az “belül”, “kívül” és “egyoldalúság” fogalma érdekes módon attól függ, hogy egy tárgy milyen környezeti térben helyezkedik el. Például egy papírlapra rajzolt huroknak (a kétdimenziós térben) van egy jól meghatározott belső és külső oldala, de egy háromdimenziós térben rajzolt huroknak nincs. Ezért nem beszélhetünk egyoldalúságról, hacsak nem döntjük el előbb, hogyan ágyazzuk be a felületet a háromdimenziós térbe. Van azonban egy szorosan kapcsolódó tulajdonság, amely az alakzat sajátja, és nem függ a környező tértől. Egy felületet orientálhatónak nevezünk, ha egy rá rajzolt alakzatot nem lehet úgy körbe és vissza csúsztatni oda, ahonnan kiindult, hogy az a saját tükörképének tűnjön. Amint a jobb oldali képet kísérő animáción látható, a Möbius-szalag nem orientálható. És ahogy a fenti mosolygós képen is láthatod, a Klein-palack sem az. hogy teljes matematikai leírását adjuk, a Klein-palack egy zárt, nem orientálható felület. Ha többet szeretnél megtudni róla, nézd meg az Inside the Klein bottle (A Klein-palack belsejében) című cikket.
A szerzőről
Marianne Freiberger a Plus szerkesztője.