A Gibbs-Helmholtz-egyenlet segítségével megkaphatjuk az \(K\)
\}{∂T} hőmérsékletfüggését. \right)_P = \dfrac{-Δ_rH^o}{T^2}\]
Egyensúlyi állapotban \(Δ_rG^o\) és \(-RT\ln K\) egyenlővé tehető, így megkapjuk:
\}{∂T} \right)_P = \dfrac{Δ_rH^o}{RT^2} \]
Láthatjuk, hogy az, hogy \(K\) nő vagy csökken a hőmérséklettel, összefügg azzal, hogy a reakcióentalpia pozitív vagy negatív. Ha a hőmérsékletet elég keveset változtatjuk ahhoz, hogy \(Δ_rH^o\) állandónak tekinthető, akkor az egyik hőmérsékleten mért \(K\) értéket a fenti kifejezés integrálásával átfordíthatjuk egy másik hőmérsékletre, hasonló levezetést kapunk, mint az olvadásponti depresszió esetén:
\
Ha nagyobb pontosságra van szükség, akkor a ΔrHo hőmérsékletváltozását korrigálhatjuk a hőkapacitási adatok felhasználásával.
Az, hogy \(K\) hogyan nő vagy csökken a hőmérséklettel, összefügg azzal, hogy a reakcióentalpia pozitív vagy negatív.
Az \(K\) kifejezés meglehetősen érzékeny függvénye a hőmérsékletnek, mivel exponenciálisan függ a sztöchiometriai együtthatók különbségétől Az egyensúlyi állandók érzékeny hőmérsékletfüggésének egyik módja az, hogy felidézzük, hogy
\
Mégis, mivel állandó nyomás és hőmérséklet mellett
\
Az \(\ref{18}\) egyenlet
\
mindkét oldal természetes logaritmusát véve, lineáris kapcsolatot kapunk az \(\ln K \)és a standard entalpiák és entrópiák között:
\
amit van’t Hoff-egyenletként ismerünk. Ez azt mutatja, hogy az \(\ln K\) és az \(1/T\) függvénye egy egyenes, amelynek meredeksége \(-\Delta_r{H^o}/R\) és metszete \(\Delta_r{S^o}/R\).
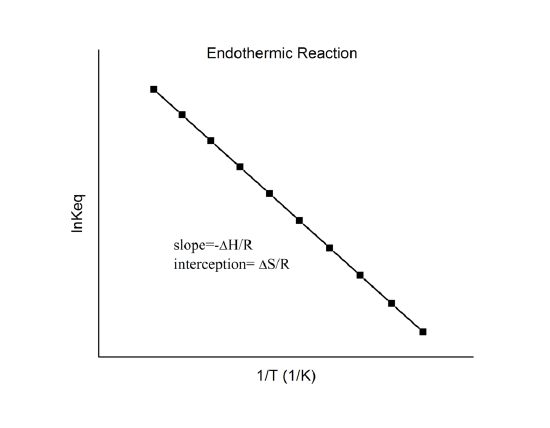
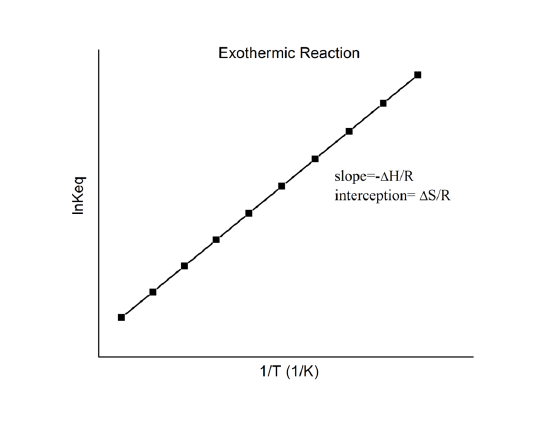
Az \(\ln K\) vs. \(1/T\) adatokból tehát kalorimetria elvégzése nélkül is meghatározhatók ezek a mennyiségek. Természetesen a fő feltételezés itt az, hogy \(\Delta_r{H^o}\) és \(\Delta_r{S^o}\) csak nagyon gyengén függ az \(T\)-től, ami általában érvényes.