¿Qué es la permeabilidad de la membrana celular?
Modo Lector
Una de las características propias de todos los organismos vivos es que contienen una mezcla distintiva de iones y pequeñas moléculas. La composición no sólo difiere del entorno, sino que también puede variar dentro de la célula. Por ejemplo, la concentración de iones de hidrógeno en algunos compartimentos celulares puede ser 104 veces mayor que en otros (las mitocondrias alcanzan un pH tan alto como 8; los lisosomas con un pH tan bajo como 4, BNID 107521, 106074). La relación de las concentraciones de iones Ca2+ en los compartimentos de fluido extra e intracelular puede ser de nuevo de 104 veces (BNID 104083). Esta diferencia de concentración es tan grande que el transporte de un ion Ca2+ a través de la membrana, desde el compartimento intracelular al extracelular, requiere la energía de más de un protón o de un ion sodio que fluye por el gradiente de fuerza motriz de protones. Para ver esto, el lector debe recordar la regla empírica de nuestra lista de trucos del oficio de que para establecer una diferencia de potencial de un orden de magnitud se necesitan 6 kJ/mol (≈2 kBT). Esta energía puede alcanzarse, por ejemplo, mediante el transporte de una carga eléctrica a través de una diferencia de potencial de 60 mV. Para conseguir una relación de concentración de cuatro órdenes de magnitud se necesitaría entonces que una carga recorriera unos 240 mV de fuerza motriz de electrones (en realidad incluso más debido a la doble carga del ion calcio). Esto está muy cerca del voltaje de ruptura de la membrana, tal y como se discute en la viñeta sobre «¿Cuál es la diferencia de potencial eléctrico a través de las membranas?». De hecho, la alta relación de concentración de Ca2+ se consigue normalmente acoplándose al transporte de tres iones de sodio o a la hidrólisis de ATP, lo que ayuda a conseguir la diferencia de densidad requerida sin energizar peligrosamente la membrana.
La segunda ley de la termodinámica nos enseña que, en general, la presencia de gradientes de concentración acabará siendo desangrada por los procesos de transporte de masa, que conducen constantemente a los sistemas a un estado de equilibrio. Sin embargo, aunque la segunda ley de la termodinámica nos indica la naturaleza del estado final de un sistema (por ejemplo, concentraciones uniformes), no nos dice cuánto tiempo llevará alcanzar ese estado. Las membranas han evolucionado hasta formar una barrera muy eficaz para la transferencia espontánea de muchas especies iónicas y moleculares. Para estimar la escala de tiempo para igualar las concentraciones, necesitamos conocer las tasas de transporte de masa, que dependen de propiedades materiales clave como las constantes de difusión y las permeabilidades.
Una clase de «leyes» de gran éxito, que describen el comportamiento de los sistemas que han sufrido alguna pequeña desviación del equilibrio, son las leyes de transporte lineal. Estas leyes plantean una relación lineal simple entre la tasa de transporte de alguna cantidad de interés y la fuerza motriz asociada. En el caso del transporte de masas, existe una relación lineal entre el flujo (es decir, el número de moléculas que atraviesan la unidad de superficie por unidad de tiempo) y la diferencia de concentración (que sirve como fuerza motriz relevante). Para el transporte a través de membranas, estas ideas se han codificado en la sencilla ecuación (para soluto neutro) j= – p-(cin-cout), donde j es el flujo neto hacia la célula, cin y cout se refieren a las concentraciones en el interior y el exterior de la región delimitada por la membrana, y p es un parámetro del material conocido como permeabilidad. Las unidades de p pueden deducirse observando que el flujo tiene unidades de número/(área x tiempo) y la concentración tiene unidades de número/volumen, lo que implica que las unidades de p son longitud/tiempo. Al igual que muchas magnitudes de transporte (por ejemplo, las conductividades eléctricas de los materiales, que abarcan más de 30 órdenes de magnitud), la permeabilidad tiene un rango dinámico muy grande, como se ilustra en la figura 1. Como se ve en la figura, las bicapas lipídicas tienen un rango de permeabilidades de casi 1010 veces.
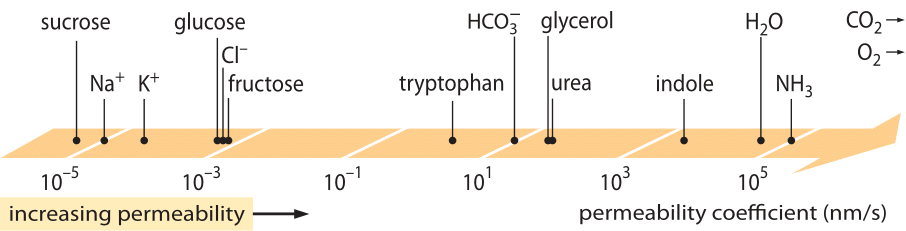
Figura 1: El amplio rango de permeabilidades de membrana de diferentes compuestos en la célula. Las membranas son más permeables a los compuestos no cargados y menos permeables a los iones cargados. Nótese que la existencia de canales iónicos hará que la permeabilidad aparente cuando están abiertos sea varios órdenes de magnitud mayor. Las unidades se han elegido como nm/s y varios nm es la anchura característica de la membrana. Figura adaptada de R. N. Robertson, The Lively Membranes, Cambridge University Press, 1983. El valor de la glucosa es menor que el de Robertson, basado en varias fuentes como BNID 110830, 110807. Otras fuentes de datos: BNID 110729, 110731, 110816, 110824, 110806.
¿Qué parámetros físico-químicos guían la ubicación de un compuesto en esta escala de permeabilidades? Una regla general es que las moléculas pequeñas tienen permeabilidades más altas que las moléculas más grandes. Otra regla general es que los compuestos neutros pueden atravesar la membrana muchos órdenes de magnitud más rápido que los compuestos con carga similar. Entre los compuestos cargados, los negativos (aniónicos) suelen tener permeabilidades mucho mayores que los positivos (catiónicos). La llamada regla de Overton establece que la permeabilidad de la membrana aumenta con la hidrofobicidad, siendo ésta la tendencia de un compuesto a preferir un disolvente no polar a un disolvente polar (acuoso). La regla de Overton predice que las moléculas cargadas (no hidrofóbicas), como los iones, tenderán a tener una baja permeabilidad, ya que incurren en una penalización energética asociada a la penetración de la membrana, mientras que los gases disueltos, como el O2 y el CO2, que son hidrofóbicos (al no estar cargados y ser simétricos), tendrán una alta permeabilidad. De hecho, la permeabilidad de las membranas de bicapa lipídica al CO2 da valores que son de 0,01-1 cm/s (sí, las mediciones de permeabilidad tienen incertidumbres muy altas entre los diferentes laboratorios, BNID 110004, 110617, 102624), más altos que todos los demás valores mostrados en la Figura 1. Este valor muestra que la barrera creada por la membrana celular es en realidad un obstáculo menor que la barrera causada por la capa de agua no agitada que envuelve la membrana celular desde el exterior. Esta deducción puede derivarse de la ecuación del coeficiente de permeabilidad de un obstáculo, dada por p=K x D/l donde l es la anchura, D el coeficiente de difusión y K el coeficiente de partición entre el medio y el material del obstáculo. Esto también se conoce como el modelo de «solubilidad-difusión» para la permeabilidad, donde se denotan los efectos K y D, que son dos pasos que afectan a la permeabilidad. Para una capa de agua no agitada, K=1, ya que es muy similar al medio, pero para las membranas, el valor para todos los materiales, excepto los más hidrofóbicos, suele ser varios órdenes de magnitud inferior a 1. Esta dependencia de K es el núcleo de la regla de Overton mencionada anteriormente. La alta permeabilidad para el CO2 también sugiere que los canales como las acuaporinas que se sugirieron para el transporte de gas en la célula no son necesarios ya que la membrana es lo suficientemente permeable. Para ver cómo las propiedades de la membrana afectan a la composición química de los metabolitos, pasamos a calcular el tiempo de fuga de diferentes compuestos
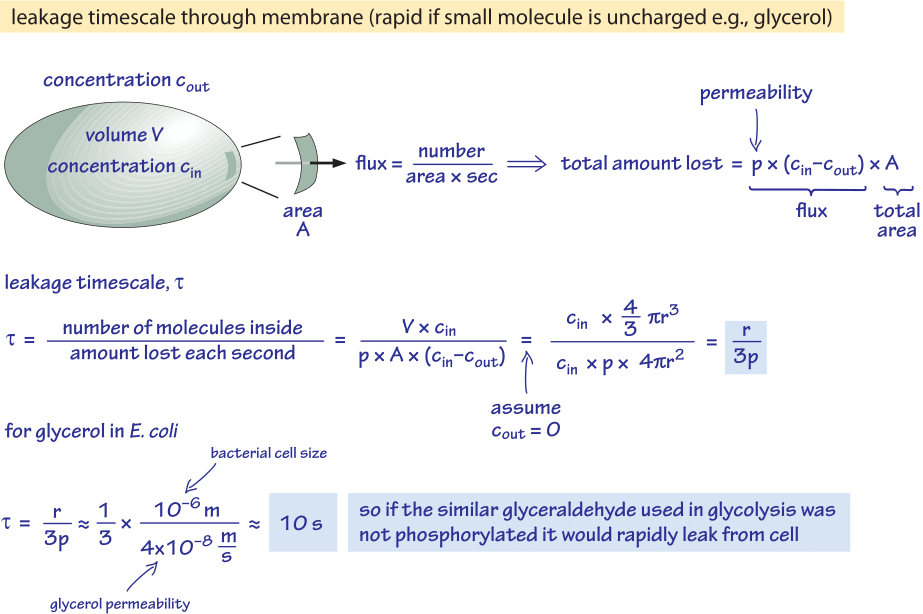
Figura 2: Cálculo de la escala de tiempo para que una molécula de glucosa no fosforilada se difunda pasivamente fuera de una célula bacteriana. Las implicaciones funcionales se consideran entonces para las células de crecimiento rápido, donde el efecto es insignificante, y para las células en estado estacionario, donde puede causar una fuga apreciable de recursos.
Consideramos el glicerol, por ejemplo. El análisis mostrado en la Figura 2 da una estimación del tiempo de su fuga fuera de la célula si la molécula no es fosforilada o convertida de otra manera en una forma más hidrofílica. La permeabilidad de la membrana celular al glicerol es de p≈10-100 nm/s (BNID 110824), como puede leerse en la Figura 1. La escala de tiempo para que una molécula de glicerol en el interior de la célula escape de nuevo al medio circundante, suponiendo que no hay flujo de retorno a la célula (cout=0), puede estimarse de forma cruda observando que el eflujo de la célula es p-A-cin donde A es el área de la superficie celular. La escala de tiempo se encuentra tomando la cantidad total en la célula, V-cin (donde V es el volumen de la célula o más exactamente el volumen de agua de la célula), y dividiendo por este flujo que resulta para una célula bacteriana (r≈1 μm) en una escala de tiempo:
t =V-cin/p-A-cin =(4πr3/3)/(4πr2-3×10-6 cm/s) ≈ 10 s.
Esta es una estimación burda porque no hemos tenido en cuenta la disminución de la concentración de cin con el tiempo que dará un factor de corrección de 1/ln(2), es decir, menos de 2 veces de aumento. Lo que aprendemos de estas estimaciones es que si los intermedios glicolíticos gliceraldehído o dihidroxiacetona, que son muy similares al glicerol, no fueran fosforilados, dando lugar a la adición de una carga, se perderían en el medio por difusión a través de la membrana celular. En los medios de laboratorio, en los que se suministra una fuente de carbono en abundancia, esto no es un problema importante, pero en un entorno natural en el que las células suelen esperar en fase estacionaria un pulso afortunado de nutrientes (se cree que E. coli se cree que pasa meses sin crecer después de su excreción del cuerpo antes de encontrar un nuevo huésped), la célula puede frenar sus pérdidas asegurándose de que los intermediarios metabólicos estén marcados con una carga que les impida volver a cruzar la barrera que presenta la bicapa lipídica.




