Presentación de la botella de Klein

Si te gusta beber, la botella de Klein no es un recipiente recomendable. Puede parecerse vagamente a una botella, pero no encierra ningún volumen, lo que significa que no puede contener ningún líquido. Lo que se vierta «dentro» simplemente volverá a salir.

¿Cómo se construye una cosa tan extraña y por qué se quiere construir? El matemático Félix Klein, que descubrió la botella en 1882, la describió como una superficie que «puede visualizarse invirtiendo un trozo de tubo de goma y dejándolo pasar a través de sí mismo para que el exterior y el interior se encuentren».

Tu navegador no admite la etiqueta de vídeo.Enlace directo

Es obvio que la botella de Klein, al igual que la esfera más conocida, es una superficie cerrada: es finita en el sentido de que se puede encajar en una región finita del espacio, pero una hormiga podría caminar por ella eternamente sin encontrar nunca un límite o caer sobre un borde. A diferencia de la esfera, que tiene un interior y un exterior, la botella de Klein es unilateral: caminando, nuestra hormiga podría alcanzar ambos lados de cada punto de la superficie. Por eso la botella no encierra ningún volumen, y también responde a la pregunta del «por qué»: la botella de Klein es interesante porque no encontramos muchas formas unilaterales en la naturaleza. (Vea aquí otra imagen muy bonita de una botella de Klein.)

La banda de Möbius es unilateral – vea la versión animada. (Imagen y animación de Konrad Polthier.)

Si esto es un poco confuso, piensa en un ejemplo más sencillo de superficie unilateral: la famosa tira de Möbius. Se puede hacer una tomando dos extremos de una tira de papel, dándole una vuelta y pegando los extremos. Si utilizas una tira de papel cuyos dos lados tengan colores diferentes, por ejemplo verde y naranja, es fácil convencerte de que la tira de Möbius resultante es unilateral. Una vez retorcida y pegada, verás que puedes llegar a cada punto naranja desde cada punto verde sin tener que atravesar el papel o trepar por su borde.

A diferencia de la botella de Klein, la tira de Möbius sí tiene un límite: está formado por los dos bordes no pegados de la tira original. Pero existe un vínculo entre ambas. Si se toman dos bandas de Möbius y se crea una forma cerrada uniendo sus límites mediante una banda ordinaria de dos lados, como se muestra a continuación, lo que se obtiene es exactamente la botella de Klein.

Su navegador no soporta la etiqueta de vídeo.Enlace directo

Este hecho inspiró al matemático Leo Moser a componer un limerick:

Un matemático llamado KleinPensó que la banda de Möbius era divina.Dijo: «Si pegas los bordes de dos, obtendrás una botella rara como la mía».

¡Algunos matemáticos son realmente polifacéticos!

Otra característica curiosa de la botella de Klein es que se interseca a sí misma, lo que significa que es difícil hacerla a partir de un solo tubo de goma como sugirió Klein. Estrictamente hablando, el objeto que se interseca a sí mismo representado arriba no es una botella de Klein, sino (como indicó Klein) sólo una visualización de una. Para entender por qué, pensemos primero en el más familiar donut (conocido matemáticamente como toro). Se puede hacer un toro a partir de una lámina cuadrada de goma pegando primero dos lados opuestos para formar un cilindro, y luego pegando los dos componentes límite de ese cilindro para obtener el toro.

Haciendo un toro: Primero pega puntos opuestos en dos lados opuestos del cuadrado para hacer un cilindro y luego pega los dos círculos de contorno de ese cilindro (correspondientes a pegar puntos opuestos en los dos lados restantes del cuadrado) para formar un toroide.

Si no quieres molestarte con el pegado, puedes simplemente pensar en el toroide como un cuadrado, teniendo en cuenta que los puntos opuestos en lados opuestos se consideran iguales. Así que cuando deslizas una forma dibujada en el «cuadrado» por el borde superior, volverá a aparecer en el borde inferior y cuando la deslizas por el borde derecho volverá a aparecer en el borde izquierdo (y viceversa).

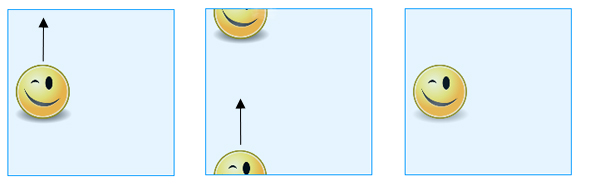
Cuando se desliza una forma dibujada en el «cuadrado» a través del borde superior, volverá a aparecer en el borde inferior.

Para obtener una verdadera botella de Klein, se empieza de la misma manera, identificando puntos opuestos en un par de lados opuestos de un cuadrado. Para el otro par de lados, sin embargo, no identifiques puntos directamente opuestos, sino puntos diagonalmente opuestos, como se muestra en la imagen.

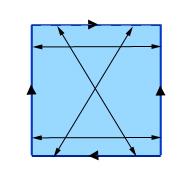
Hacer una botella de Klein: identifica los puntos opuestos de dos lados opuestos (los verticales en esta imagen) y luego identifica los puntos diagonalmente opuestos en los dos lados restantes. (Si etiquetas los puntos de los lados superior e inferior de izquierda a derecha con los números del 0 al 1, entonces un punto con la etiqueta x en el lado superior se identifica con el punto con la etiqueta 1-x en el lado inferior.)

El objeto resultante es la botella de Klein. De nuevo, puedes pensar en ella como un cuadrado, teniendo en cuenta que los puntos límite se consideran iguales. Si deslizas una forma sobre uno de los bordes que tenía identificados los puntos opuestos (el vertical en nuestra imagen), vuelve a aparecer en el lado opuesto, como antes. Si, por el contrario, la deslizas sobre una de las aristas cuyos puntos estaban identificados en diagonal (horizontal en nuestra imagen), aparece en el lado opuesto, pero desplazada y como una imagen especular de su ser original.

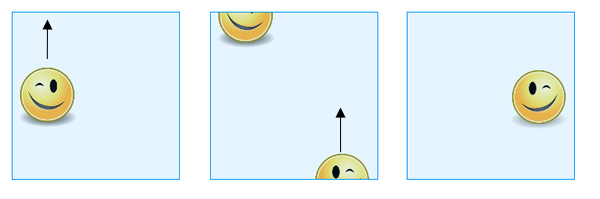
Si deslizas una forma por el borde superior, aparece por el borde inferior, pero desplazada hacia el otro lado y como una imagen especular de su ser original.

La única manera de construir esta forma en el espacio tridimensional pegando realmente los puntos es permitir que se intersecte a sí misma. Esto equivale a identificar pares de puntos en el interior del cuadrado original, por lo que estrictamente hablando la forma resultante no es exactamente la misma que la botella de Klein, que sólo tiene identificados los puntos límite. Es sólo una forma de representar la botella en el espacio tridimensional (también hay otras).

Curiosamente, los conceptos de «interior», «exterior» y «unilateralidad» dependen del espacio ambiental en el que se encuentra un objeto. Por ejemplo, un bucle dibujado en un papel (en un espacio bidimensional) tiene un interior y un exterior bien definidos, pero un bucle dibujado en un espacio tridimensional no. Por eso no podemos hablar de unilateralidad si no decidimos primero cómo incrustar una superficie en el espacio tridimensional. Sin embargo, existe una propiedad estrechamente relacionada que es intrínseca a una forma y no depende del espacio circundante. Una superficie se llama orientable si no se puede deslizar una forma dibujada en ella alrededor y de vuelta al punto de partida para que parezca su propia imagen especular. Como puedes ver en la animación que acompaña a la imagen de la derecha, la banda de Möbius no es orientable. Y como puedes ver en la imagen con la cara sonriente de arriba, tampoco lo es la botella de Klein.Para darle su descripción matemática completa, la botella de Klein es una superficie cerrada y no orientable. Para saber más sobre ella, consulta el artículo Dentro de la botella de Klein.

Acerca del autor

Marianne Freiberger es editora de Plus.