Pearson Mode Skewness

Definiciones de Estadística >Pearson Mode Skewness

Pearson mode skewness, también llamado primer coeficiente de asimetría de Pearson, es una forma de averiguar la asimetría de una distribución.

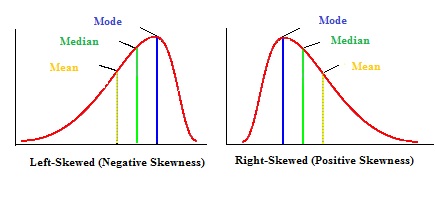
La media, la moda y la mediana se pueden utilizar para averiguar si se tiene una distribución sesgada positiva o negativamente.

• Si la media es mayor que la moda, la distribución está sesgada positivamente.
• Si la media es menor que la moda, la distribución está sesgada negativamente.
• Si la media es mayor que la mediana, la distribución es sesgada positivamente.
• Si la media es menor que la mediana, la distribución es sesgada negativamente.

La asimetría del modo de Pearson

La asimetría del modo de Pearson utiliza los hechos anteriores para ayudarle a averiguar si tiene asimetría positiva o negativa. Si tiene una distribución y conoce la media, la moda y la desviación estándar (σ), entonces la fórmula de asimetría del modo de Pearson es:

(media-modo)/σ

Problema de la muestra: Tiene datos con una media de 19, una moda de 20 y una desviación estándar de 25. ¿Qué le dice la asimetría del modo de Pearson sobre la distribución?
(media-modo)/σ = (19-20)/25 = -0,04.
Hay una asimetría negativa muy ligera (-0,04). Nota: Para la mayoría de los intentos y propósitos, esto contaría como una distribución simétrica ya que la asimetría es muy pequeña.

Asimetría del modo de Pearson: Fórmula alternativa.

Si no conoce la moda, no podrá utilizar la asimetría del modo de Pearson. Sin embargo, la dirección de la asimetría también se puede averiguar encontrando dónde están la media y la mediana. Según Business Statistics, esto conduce a una segunda fórmula equivalente:

3(Media – Mediana) / σ

Esta fórmula también se llama segundo coeficiente de asimetría de Pearson.

Asimetría del modo de Pearson: Qué significan los resultados.

La diferencia entre la media y la moda, o la media y la mediana, le indicará cuánto se aleja la distribución de la simetría. Una distribución simétrica (por ejemplo, la distribución normal) tiene una asimetría de cero.
Ambas ecuaciones le dan resultados en desviaciones estándar, que son unidades adimensionales de medida de la media.

Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Klein, G. (2013). La introducción de dibujos animados a la estadística. Hill & Wamg.
Vogt, W.P. (2005). Diccionario de estadística &Metodología: Una guía no técnica para las ciencias sociales. SAGE.

——————————————————————————

¿Necesitas ayuda con los deberes o con un examen? Con Chegg Study, puede obtener soluciones paso a paso a sus preguntas de un experto en la materia. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!