Antes de empezar tenemos que hacer algunas suposiciones.
En primer lugar, estamos trabajando con fluidos newtonianos. Esta es la forma matemática más sencilla de tener en cuenta la viscosidad en un fluido. No hay fluidos reales que entren perfectamente en esta categoría, pero en la mayoría de los casos, el aire y el agua pueden ser tratados como un fluido newtoniano. La otra hipótesis muy importante que planteamos es que el fluido es incompresible. Esto significa que su densidad, rho, es una constante.
Conservación de la masa

La primera ecuación nos dice que la masa del fluido con el que estamos trabajando se conserva. El fluido puede cambiar de forma pero esta ecuación nos dice que la masa es la misma de principio a fin.
Ahora hablemos de matemáticas. La letra u representa la velocidad del fluido y es un vector. Tiene tres componentes, podemos llamarlas u, v, w y representan la velocidad del fluido en la dirección x, y y z. La letra griega nabla ∇ seguida de un punto es el operador de divergencia. Esto significa que tenemos que diferenciar sus componentes en cada dirección (en este caso x, y, z).

La primera derivada nos está diciendo cómo cambia la componente x de la velocidad a medida que nos movemos en la dirección x. Lo mismo ocurre con las otras dos derivadas. Como esta ecuación es igual a cero, nos está mostrando que la masa se conserva.
Conservación del momento

La segunda ecuación es en realidad un conjunto de tres ecuaciones diferenciales. Es la que se puede describir como la segunda ley de Newton para los fluidos. Si expandimos la expresión obtenemos un sistema complejo.
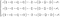
Puesto que es mucho más sencilla de entender, vamos a concentrarnos en la conservación del momento no expandida.
Cuando trabajamos con fluidos podemos decir que masa y densidad son lo mismo (siempre que su volumen sea el mismo). Si consideramos dos fluidos, podemos decir que el más denso es el más «pesado» (por ejemplo, el mercurio y el agua). En este caso, la letra griega ρ (rho) es la densidad del fluido.
Tenemos la masa, ahora para volver a la segunda ley de Newton necesitamos la aceleración. Que es exactamente el resultado de la derivada temporal del vector velocidad.

Ahora sólo nos quedan los términos del lado derecho del signo igual, y esos representan todas las fuerzas que se aplican al fluido.
El primer término ∇p es el gradiente de la presión. Representa la diferencia de presión en el espacio donde está contenido el fluido. Por ejemplo, si hay una zona con baja presión y otra con una presión más alta el fluido se moverá desde la sección de alta presión a la más baja. El gradiente de p está diciendo todo eso.
El segundo término describe la viscosidad del fluido. Piensa en dos líquidos diferentes, como el agua y la miel. Cuando se vierte un vaso de agua, ésta cae rápida y fácilmente. Cuando haces lo mismo con la miel, ésta es pegajosa y se vierte muy lentamente. Esto es lo que dice esa expresión.
El último término, F, es el más fácil porque representa todas las fuerzas externas que se pueden aplicar a ese fluido. Normalmente, la fuerza que consideramos aquí es la gravedad.
Esto es todo, todos esos símbolos extravagantes y el significado de las letras es simplemente fuerza = masa x aceleración.
Uso de las ecuaciones de Navier-Stokes
Como la resolución de estas ecuaciones es tan complicada, para usarlas tenemos que hacer muchas aproximaciones. Algunos ejemplos son el flujo de Poiseuille y el de Couette. Con muchas suposiciones, estos dos científicos fueron capaces de encontrar una solución a las ecuaciones de Navier-Stokes para una aplicación muy específica. Sin embargo, si queremos utilizarlas para una tarea más complicada, como las previsiones meteorológicas, tenemos que hacer algo más.
La forma más común de utilizar estas ecuaciones es transformándolas, con la media de Reynolds. Este es un proceso matemático avanzado y los resultados son las ecuaciones de Reynolds. Suelen llamarse ecuaciones RANS (que significa Navier-Stokes promediado por Reynolds).
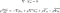
Estas ecuaciones se utilizan cuando el fluido está en un flujo turbulento. Son casi idénticas a las ecuaciones de Navier-Stokes, excepto por el último término. Éste se llama tensor de tensión de Reynolds. Es la cantidad que nos permite tener en cuenta la turbulencia en el fluido.
En las ecuaciones RANS, las cantidades que utilizamos se promedian en un intervalo de tiempo. Este intervalo tiene que ser lo suficientemente pequeño como para permitir la observación del fenómeno que estamos estudiando. Al mismo tiempo, tiene que ser lo suficientemente grande para que el efecto de la turbulencia pierda importancia.
Con las suposiciones correctas, estas ecuaciones funcionan. Sabemos cómo utilizarlas para que los coches de F1 sean más rápidos, para que una nave espacial vaya a la ISS y para hacer la previsión del tiempo. Así que te preguntarás ¿por qué la prueba de estas ecuaciones vale un millón de dólares?
Un premio de un millón de dólares
Desde el punto de vista de la física, estas ecuaciones no son más que la segunda ley de Newton que funciona con fluidos. Cuando hacemos algunas suposiciones y algunas simplificaciones, podemos hacer cosas sorprendentes con ellas.
El verdadero problema es este. Resolver estas ecuaciones sin aproximaciones es terriblemente complicado. Es tan difícil que no se ha demostrado que las soluciones existan realmente. Y aquí es donde entra el Premio del Milenio.
El enunciado oficial del problema (encuéntralo aquí) es:
Demostrar o dar un contraejemplo del siguiente enunciado: en tres dimensiones espaciales y temporales, dado un campo de velocidad inicial, existe un campo de velocidad vectorial y un campo de presión escalar, que son suaves y globalmente definidos, que resuelven las ecuaciones de Navier-Stokes.
Lo que esto significa es que para ganar el premio hay que hacer tres cosas:
- Demostrar que existe una solución
- La solución tiene que existir en cada punto del espacio
- La solución tiene que ser suave. Esto significa que un pequeño cambio en las condiciones iniciales produce sólo una pequeña variación del resultado.
Para un ingeniero suele ser suficiente saber que estas ecuaciones funcionan, aunque sólo sea hasta cierto nivel de aproximación. Sin embargo, para un matemático es muy importante saber si las soluciones existen y cómo se comportan.
Ahora estarás pensando que si funcionan tal cual, gastar tiempo y energía en buscar una demostración es una total pérdida de tiempo. Bueno, como muchos avances tecnológicos en la historia de la humanidad el resultado puede no parecer muy importante. Lo importante es el camino para llegar a él, que puede aportar nuevos conocimientos y mejoras a nuestra vida.
Piensa en las misiones espaciales. Si el ser humano nunca decidiera ir a pisar la luna no tendríamos muchos objetos que sirven para mejorar nuestra vida. Las máquinas de resonancia magnética y los marcapasos provienen de tecnologías desarrolladas para la exploración espacial. Hoy los médicos de todo el mundo los utilizan a diario para salvar vidas. Lo mismo ocurre aquí. El camino hacia el descubrimiento de la solución de las ecuaciones de Navier-Stokes nos ayudará a mejorar nuestra comprensión de los fluidos y mucho más. Puede llevarnos a nuevos descubrimientos y probablemente requerirá la invención de nuevas matemáticas. Esto puede servir para responder a muchos otros problemas, para inventar nuevas tecnologías que mejoren nuestra vida y nos hagan mejores.