Construir Triángulo Equilátero – MathBitsNotebook (Geo

Triángulo Equilátero MathBitsNotebook.com Contorno Temático |Contorno de Geometría | Recursos para Profesores de MathBits Términos de Uso Persona de Contacto: Donna Roberts

Usa sólo tu compás y tu regla cuando dibujes una construcción. No dibujes a mano alzada

Haremos TRES construcciones de un triángulo equilátero. La primera será construir un triángulo equilátero dada la longitud de un lado, y las otras dos serán construir un triángulo equilátero inscrito en una circunferencia.

Dado: la longitud de un lado del triángulo Construye: un triángulo equilátero

Pasos:
1. Coloca la punta del compás en A y mide la distancia al punto B. Gira un arco de esta medida por encima (o por debajo) del segmento.
2. Sin cambiar el tramo en el compás, coloca la punta del compás en B y gira el mismo arco, intersectando con el primer arco.
3. Etiquetar el punto de intersección como el tercer vértice del triángulo equilátero.

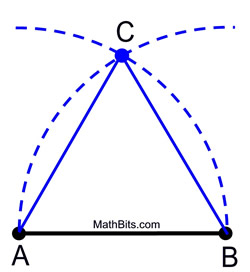Ver los círculos completos en funcionamiento.

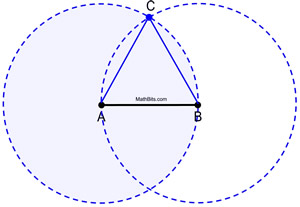
Prueba de la construcción: La circunferencia A es congruente con la circunferencia B, ya que cada una se formó utilizando la misma longitud de radio, AB. Como AB y AC son longitudes de radios del círculo A, son iguales entre sí. Del mismo modo, AB y BC son radios del círculo B, y son iguales entre sí. Por tanto, AB = AC = BC por sustitución (o propiedad transitiva). Como los segmentos congruentes tienen longitudes iguales, y ΔABC es equilátero (tiene tres lados congruentes).

Pasos:
1. Coloca la punta de tu compás en el papel y dibuja un círculo. (¡Mantenga este compás!)
2. Coloque un punto, etiquetado como A, en cualquier parte de la circunferencia del círculo para que sirva de punto de partida.
3. Sin cambiar la amplitud del compás, coloca la punta del compás en A y haz un pequeño arco que cruce la circunferencia del círculo.
4. Sin cambiar la amplitud del compás, mueve la punta del compás a la intersección del arco anterior y la circunferencia y haz otro pequeño arco en la circunferencia del círculo.
5. Sigue repitiendo este proceso de «paso» alrededor del círculo hasta que vuelvas al punto A.
6. Partiendo de A, conecta todos los demás arcos del círculo para formar el triángulo equilátero.

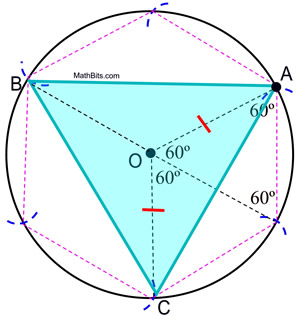Consulte la prueba de un hexágono regular inscrito para obtener más información relativa a la prueba de esta construcción.

Prueba de la construcción: La prueba del hexágono regular inscrito muestra que los ángulos centrales de un hexágono regular contienen 60º. Los ángulos centrales del triángulo inscrito en esta circunferencia contienen 120º. Como ΔAOC es isósceles (OA y OC son longitudes de radio), m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC ΔCOB ΔBOA por SAS. Por CPCTC, ∠OCB ∠OCA y m∠OCB = 30º por sustitución y m∠BCA = 60º. De forma similar, tenemos m∠ACB = m∠CBA = m∠BAC = 60º y el equilátero ΔABC.

PASOS:
1. Coloca la punta del compás en el papel y dibuja una circunferencia, O. (¡Mantén esta luz del compás!)
2. Con una regla, dibuja un diámetro de la circunferencia, rotulando los puntos extremos P y B.
3. Sin cambiar la luz del compás, coloca la punta del compás en P y dibuja una circunferencia completa.
4. Rotula los puntos de intersección de las dos circunferencias con A y C.
5. Dibuja segmentos de A a B, de B a C y de C a A, para formar el triángulo equilátero.

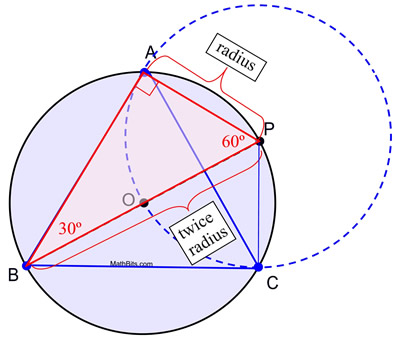
Prueba de la construcción: Esta construcción utiliza el hecho de que un ángulo inscrito en una semicircunferencia es un ángulo recto, y que en un triángulo 30º-60º-90º, la longitud del cateto corto es la mitad de la longitud de la hipotenusa. En esta construcción, el círculo O y el círculo P son congruentes ya que tienen la misma longitud de radio. AP es una longitud de radio del círculo P y los radios AP = OP. OP también es una longitud de radio del círculo O (junto con OB) y el diámetro BP = BO + OP = 2 OP. Por sustitución, BP = 2 AP, creando las condiciones necesarias para m∠ABP = 30º. En consecuencia, m∠APB = 60º. Un argumento similar puede utilizarse para establecer que para ΔPBC, m∠PBC = 30º y m∠BPC = 60º haciendo que ΔPBC ΔPBA por ASA (con lado compartido de B a P).
Ahora, ya que son los lados correspondientes de los dos triángulos congruentes, haciendo que ΔABC sea isósceles. ∠BAC ∠BCA ya que los ángulos de la base de un triángulo isósceles son congruentes.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º por postulado de adición de ángulos y sustitución. m∠BAC + m∠BCA + m∠ABC = 180º porque la suma de las medidas de los ángulos de un triángulo es 180º. Como m∠BAC + m∠BAC + 60º = 180º por sustitución, sabemos que 2m∠BAC = 120º y m∠BAC = 60º. En consecuencia m∠BCA también es igual a 60º por sustitución, con lo que ΔABC es equilátero.