Introducción
Imagínese esto – Se le ha encargado la tarea de predecir el precio del próximo iPhone y se le han proporcionado datos históricos. Esto incluye características como las ventas trimestrales, el gasto mensual y toda una serie de cosas que vienen con el balance de Apple. Como científico de datos, ¿en qué tipo de problema clasificaría esto? Modelado de series temporales, por supuesto.
Desde la predicción de las ventas de un producto hasta la estimación del uso de la electricidad en los hogares, la previsión de series temporales es una de las habilidades fundamentales que se espera que cualquier científico de datos conozca, si no domina. Hay una gran cantidad de técnicas diferentes que se pueden utilizar, y vamos a cubrir uno de los más eficaces, llamado Auto ARIMA, en este artículo.

Primero vamos a entender el concepto de ARIMA que nos llevará a nuestro tema principal – Auto ARIMA. Para solidificar nuestros conceptos, tomaremos un conjunto de datos y lo implementaremos tanto en Python como en R.
Tabla de contenido
- ¿Qué es una serie temporal?
- Métodos de previsión de series temporales
- Introducción a ARIMA
- Pasos para la implementación de ARIMA
- ¿Por qué necesitamos AutoARIMA?
- Implementación de Auto ARIMA (en el conjunto de datos de pasajeros aéreos)
- ¿Cómo selecciona los parámetros Auto ARIMA?
Si está familiarizado con las series temporales y sus técnicas (como la media móvil, el suavizado exponencial y ARIMA), puede pasar directamente a la sección 4. Para los principiantes, empiece por la sección siguiente, que es una breve introducción a las series temporales y a varias técnicas de previsión.
¿Qué es una serie temporal?
Antes de conocer las técnicas para trabajar con datos de series temporales, debemos entender primero qué es una serie temporal y en qué se diferencia de cualquier otro tipo de datos. Esta es la definición formal de serie temporal: es una serie de puntos de datos medidos a intervalos de tiempo constantes. Esto significa simplemente que determinados valores se registran a un intervalo constante que puede ser horario, diario, semanal, cada 10 días, etc. Lo que diferencia a las series temporales es que cada punto de datos de la serie depende de los puntos de datos anteriores. Comprendamos la diferencia con mayor claridad tomando un par de ejemplos.
Ejemplo 1:
Suponga que tiene un conjunto de datos de personas que han tomado un préstamo de una determinada empresa (como se muestra en la tabla siguiente). ¿Cree que cada fila estará relacionada con las filas anteriores? Desde luego que no. El préstamo tomado por una persona se basará en sus condiciones y necesidades financieras (podría haber otros factores como el tamaño de la familia, etc., pero para simplificar estamos considerando sólo los ingresos y el tipo de préstamo) . Además, los datos no se recogieron en un intervalo de tiempo concreto. Depende del momento en que la empresa recibió una solicitud de préstamo.

Ejemplo 2:
Tomemos otro ejemplo. Supongamos que tiene un conjunto de datos que contiene el nivel de CO2 en el aire por día (captura de pantalla de abajo). ¿Será capaz de predecir la cantidad aproximada de CO2 para el día siguiente mirando los valores de los últimos días? Por supuesto. Si observas, los datos se han registrado diariamente, es decir, el intervalo de tiempo es constante (24 horas).

Ya debes haber intuido esto: el primer caso es un simple problema de regresión y el segundo es un problema de series temporales. Aunque el rompecabezas de las series temporales también puede resolverse utilizando la regresión lineal, pero no es realmente el mejor enfoque, ya que descuida la relación de los valores con todos los valores pasados relativos. Veamos ahora algunas de las técnicas comunes utilizadas para resolver problemas de series temporales.
Métodos para la previsión de series temporales
Hay una serie de métodos para la previsión de series temporales y los cubriremos brevemente en esta sección. La explicación detallada y los códigos de python para todas las técnicas mencionadas a continuación se pueden encontrar en este artículo: 7 técnicas para la previsión de series temporales (con códigos de python).
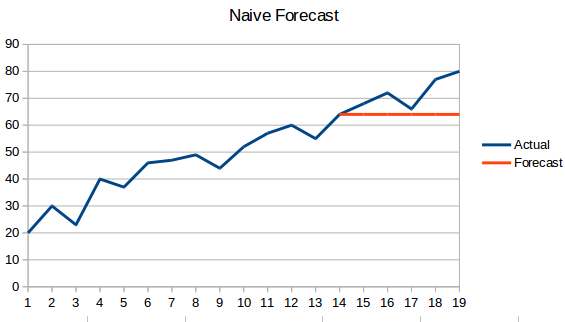
- Enfoque ingenuo: En esta técnica de previsión, se predice que el valor del nuevo punto de datos es igual al punto de datos anterior. El resultado sería una línea plana, ya que todos los nuevos valores toman los valores anteriores.
- Media simple: El siguiente valor se toma como la media de todos los valores anteriores. Las predicciones aquí son mejores que las del ‘Enfoque ingenuo’, ya que no da lugar a una línea plana, pero aquí se tienen en cuenta todos los valores anteriores, lo que puede no ser siempre útil. Por ejemplo, cuando se pide que se prediga la temperatura de hoy, se tendría en cuenta la temperatura de los últimos 7 días en lugar de la temperatura de hace un mes.

- Media móvil : Se trata de una mejora respecto a la técnica anterior. En lugar de tomar la media de todos los puntos anteriores, se toma la media de ‘n’ puntos anteriores para que sea el valor predicho.

- Media móvil ponderada : Una media móvil ponderada es una media móvil en la que los ‘n’ valores pasados reciben diferentes pesos.

- Suavizado exponencial simple: En esta técnica, se asignan mayores pesos a las observaciones más recientes que a las observaciones del pasado lejano.

- Modelo de tendencia lineal de Holt: Este método tiene en cuenta la tendencia del conjunto de datos. Por tendencia se entiende la naturaleza creciente o decreciente de la serie. Supongamos que el número de reservas de un hotel aumenta cada año, entonces podemos decir que el número de reservas muestra una tendencia creciente. La función de previsión en este método es una función de nivel y tendencia.

- Método de Holt Winters: Este algoritmo tiene en cuenta tanto la tendencia como la estacionalidad de la serie. Por ejemplo – el número de reservas en un hotel es alto los fines de semana & bajo entre semana, y aumenta cada año; existe una estacionalidad semanal y una tendencia creciente.

- ARIMA: ARIMA es una técnica muy popular para la modelización de series temporales. Describe la correlación entre puntos de datos y tiene en cuenta la diferencia de los valores. Una mejora de ARIMA es SARIMA (o ARIMA estacional). Veremos el ARIMA con un poco más de detalle en la siguiente sección.
Introducción al ARIMA
En esta sección haremos una rápida introducción al ARIMA que será útil para entender el Auto Arima. Una explicación detallada de Arima, los parámetros (p,q,d), los gráficos (ACF PACF) y la implementación se incluye en este artículo : Tutorial completo de Series Temporales.
ARIMA es un método estadístico muy popular para la previsión de series temporales. ARIMA significa medias móviles integradas autorregresivas. Los modelos ARIMA funcionan con los siguientes supuestos –
- La serie de datos es estacionaria, lo que significa que la media y la varianza no deben variar con el tiempo. Una serie puede hacerse estacionaria utilizando una transformación logarítmica o diferenciando la serie.
- Los datos proporcionados como entrada deben ser una serie univariante, ya que arima utiliza los valores pasados para predecir los valores futuros.
ARIMA tiene tres componentes – AR (término autorregresivo), I (término de diferenciación) y MA (término de media móvil). Entendamos cada uno de estos componentes –
- El término AR se refiere a los valores pasados utilizados para predecir el siguiente valor. El término AR se define por el parámetro ‘p’ en arima. El valor de ‘p’ se determina utilizando el gráfico PACF.
- El término MA se utiliza para definir el número de errores de previsión pasados utilizados para predecir los valores futuros. El parámetro ‘q’ en arima representa el término MA. El gráfico ACF se utiliza para identificar el valor correcto de ‘q’.
- El orden de diferenciación especifica el número de veces que se realiza la operación de diferenciación en la serie para hacerla estacionaria. Pruebas como ADF y KPSS pueden utilizarse para determinar si la serie es estacionaria y ayudar a identificar el valor d.
Pasos para la implementación de ARIMA
Los pasos generales para implementar un modelo ARIMA son –
- Cargar los datos: El primer paso para la construcción del modelo es, por supuesto, cargar el conjunto de datos
- Preprocesamiento: Dependiendo del conjunto de datos, se definirán los pasos del preprocesamiento. Esto incluirá la creación de marcas de tiempo, la conversión del tipo de columna de fecha/hora, hacer que las series sean univariantes, etc.
- Hacer que las series sean estacionarias: Para satisfacer el supuesto, es necesario hacer que la serie sea estacionaria. Esto incluiría comprobar la estacionariedad de la serie y realizar las transformaciones necesarias
- Determinar el valor de d: Para hacer estacionaria la serie, se tomará como valor d el número de veces que se realizó la operación de diferencia
- Crear gráficos ACF y PACF: Este es el paso más importante en la implementación de ARIMA. Los gráficos ACF PACF se utilizan para determinar los parámetros de entrada para nuestro modelo ARIMA
- Determinar los valores de p y q: Lea los valores de p y q de los gráficos del paso anterior
- Ajuste el modelo ARIMA: Utilizando los datos procesados y los valores de los parámetros que hemos calculado en los pasos anteriores, ajustar el modelo ARIMA
- Predecir los valores en el conjunto de validación: Predecir los valores futuros
- Calcular el RMSE: Para comprobar el rendimiento del modelo, compruebe el valor del RMSE utilizando las predicciones y los valores reales en el conjunto de validación
¿Por qué necesitamos Auto ARIMA?
Aunque ARIMA es un modelo muy potente para predecir los datos de las series temporales, los procesos de preparación de los datos y de ajuste de los parámetros acaban consumiendo mucho tiempo. Antes de implementar ARIMA, es necesario hacer que las series sean estacionarias y determinar los valores de p y q utilizando los gráficos que hemos comentado anteriormente. Auto ARIMA nos simplifica mucho esta tarea ya que elimina los pasos 3 a 6 que vimos en la sección anterior. A continuación se detallan los pasos que debes seguir para implementar el auto ARIMA:
- Carga los datos: Este paso será el mismo. Cargue los datos en su cuaderno
- Preprocesamiento de datos: La entrada debe ser univariante, por lo tanto, elimine las otras columnas
- Ajustar Auto ARIMA: Ajustar el modelo en la serie univariante
- Predecir valores en el conjunto de validación: Realiza predicciones sobre el conjunto de validación
- Calcula el RMSE: Comprueba el rendimiento del modelo utilizando los valores predichos frente a los valores reales
Nos saltamos completamente la selección de la característica p y q como puedes ver. ¡Qué alivio! En la siguiente sección, implementaremos el auto ARIMA utilizando un conjunto de datos de juguete.
Implementación en Python y R
Utilizaremos el conjunto de datos International-Air-Passenger. Este conjunto de datos contiene el total mensual del número de pasajeros (en miles). Tiene dos columnas: mes y número de pasajeros. Puede descargar el conjunto de datos desde este enlace.
#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)
output -76.51355764316357
A continuación se muestra el código R para el mismo problema:
# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)
¿Cómo selecciona Auto Arima los mejores parámetros
En el código anterior, simplemente utilizamos el comando .fit() para ajustar el modelo sin tener que seleccionar la combinación de p, q, d. Pero, ¿cómo averiguó el modelo la mejor combinación de estos parámetros? Auto ARIMA tiene en cuenta los valores AIC y BIC generados (como puede ver en el código) para determinar la mejor combinación de parámetros. Los valores AIC (Akaike Information Criterion) y BIC (Bayesian Information Criterion) son estimadores para comparar modelos. Cuanto más bajos sean estos valores, mejor es el modelo.
Consulte estos enlaces si está interesado en las matemáticas que hay detrás del AIC y el BIC.
Notas finales y lecturas adicionales
He encontrado que el auto ARIMA es la técnica más sencilla para realizar previsiones de series temporales. Conocer un atajo es bueno pero estar familiarizado con las matemáticas que hay detrás es también importante. En este artículo he repasado los detalles del funcionamiento de ARIMA, pero asegúrese de consultar los enlaces que aparecen en el artículo. Para su fácil referencia, aquí están los enlaces de nuevo:
- Una guía completa para los principiantes a la previsión de series de tiempo en Python
- Tutorial completo a las series de tiempo en R
- 7 técnicas para la previsión de series de tiempo (con códigos de python)
Sugeriría practicar lo que hemos aprendido aquí en este problema de práctica: Problema de práctica de series de tiempo. También puede tomar nuestro curso de formación creado sobre el mismo problema de práctica, Predicción de series temporales, para proporcionarle una ventaja.