Podemos utilizar Gibbs-Helmholtz para obtener la dependencia de la temperatura de \(K\)
{{∂T} \right)_P = \dfrac{-Δ_rH^o}{T^2}]
En el equilibrio, podemos igualar \(Δ_rG^o\️) a \(-RT\ln K\️) por lo que obtenemos:
{∂T} \right)_P = \dfrac{Δ_rH^o}{RT^2} \N-[2592>
Vemos que el hecho de que \N(K\) aumente o disminuya con la temperatura está ligado a que la entalpía de reacción sea positiva o negativa. Si la temperatura se modifica lo suficientemente poco como para que \(Δ_rH^o\) pueda considerarse constante, podemos trasladar un valor de \(K\) a una temperatura a otra integrando la expresión anterior, obtenemos una derivación similar a la de la depresión del punto de fusión:
\
Si se requiere más precisión podríamos corregir los cambios de temperatura de ΔrHo utilizando datos de capacidad calorífica.
La forma en que \(K\) aumenta o disminuye con la temperatura está relacionada con que la entalpía de reacción sea positiva o negativa.
La expresión para \(K\) es una función bastante sensible de la temperatura dada su dependencia exponencial de la diferencia de coeficientes estequiométricos Una forma de ver la dependencia sensible de la temperatura de las constantes de equilibrio es recordar que
Sin embargo, ya que bajo presión y temperatura constantes
\
La ecuación \(\ref{18}\) se convierte en
\
Tomando el logaritmo natural de ambos lados, obtenemos una relación lineal entre \(\ln K \)y las entalpías y entropías estándar:
\
que se conoce como la ecuación de van’t Hoff. Muestra que un gráfico de \(\ln K\) frente a \(1/T\) debe ser una línea con pendiente \(-\Delta_r{H^o}/R\) e intercepción \(\Delta_r{S^o}/R).
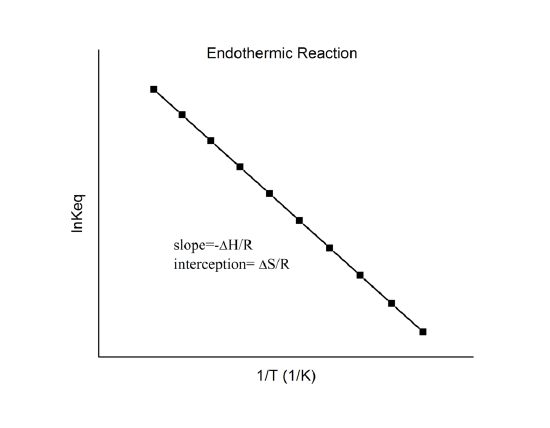
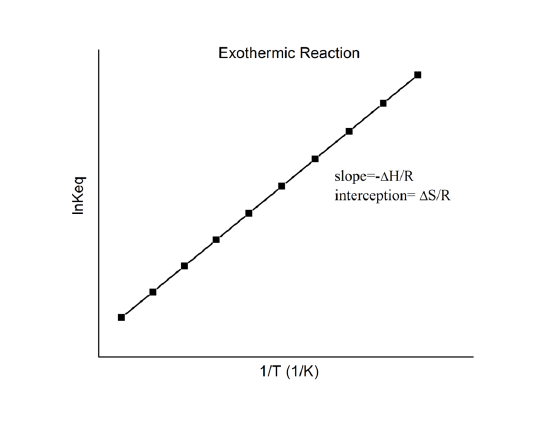
Por lo tanto, estas cantidades se pueden determinar a partir de los datos de \(\ln K\) vs. \(1/T\) sin hacer calorimetría. Por supuesto, la suposición principal aquí es que \(\Delta_r{H^o}) y \(\Delta_r{S^o}) son sólo muy débilmente dependiente de \(T\), que suele ser válido.