Describiremos tres ejemplos de las ciencias de la vida: uno de física, otro relacionado con la genética y otro de un experimento con ratones. Son muy diferentes, pero acabamos utilizando la misma técnica estadística: el ajuste de modelos lineales. Los modelos lineales suelen enseñarse y describirse en el lenguaje del álgebra matricial.
Ejemplos motivadores
Objetos que caen
Imagina que eres Galileo en el siglo XVI intentando describir la velocidad de un objeto que cae. Un ayudante sube a la Torre de Pisa y deja caer una bola, mientras otros ayudantes registran la posición en diferentes momentos. Simulemos algunos datos utilizando las ecuaciones que conocemos hoy en día y añadiendo algún error de medición:
set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##metersLos ayudantes le entregan los datos a Galileo y esto es lo que ve:
mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")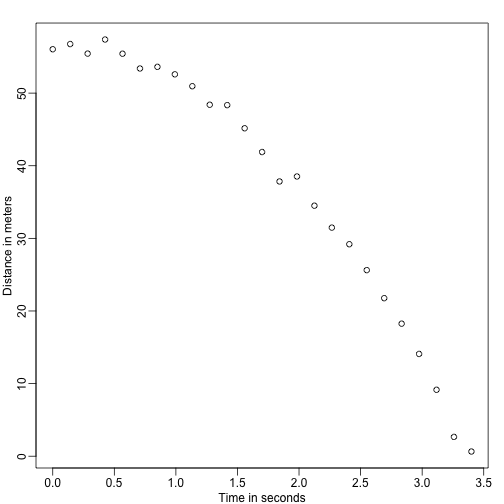
No conoce la ecuación exacta, pero observando el gráfico anterior deduce que la posición debe seguir una parábola. Así que modela los datos con:
Con representando la ubicación, representando el tiempo, y teniendo en cuenta el error de medición. Se trata de un modelo lineal porque es una combinación lineal de cantidades conocidas (las s) denominadas predictores o covariables y parámetros desconocidos (las s).
Altura del padre &y del hijo
Imagina ahora que eres Francis Galton en el siglo XIX y recoges datos de altura emparejados de padres e hijos. Sospechas que la altura se hereda. Sus datos:
library(UsingR)x=father.son$fheighty=father.son$sheightse parecen a esto:
plot(x,y,xlab="Father's height",ylab="Son's height")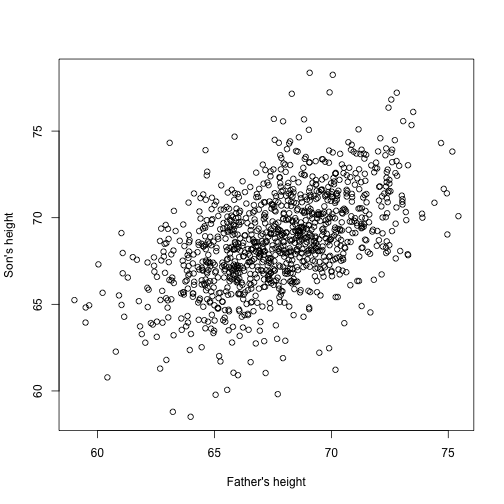
La altura de los hijos parece aumentar linealmente con la del padre. En este caso, un modelo que describe los datos es el siguiente:
También se trata de un modelo lineal con y , las alturas del padre y del hijo respectivamente, para el -ésimo par y un término para dar cuenta de la variabilidad extra. Aquí pensamos que las alturas del padre son el predictor y que son fijas (no aleatorias), por lo que utilizamos las minúsculas. El error de medición no puede explicar por sí solo toda la variabilidad observada en . Esto tiene sentido ya que hay otras variables que no están en el modelo, por ejemplo, las alturas de las madres, la aleatoriedad genética y los factores ambientales.
Muestras aleatorias de múltiples poblaciones
Aquí leemos los datos de peso corporal de ratones que fueron alimentados con dos dietas diferentes: alta en grasas y control (chow). Tenemos una muestra aleatoria de 12 ratones para cada uno. Estamos interesados en determinar si la dieta tiene un efecto sobre el peso. Estos son los datos:
dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")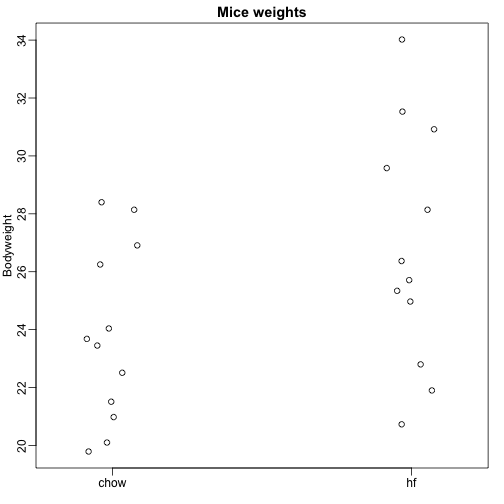
Queremos estimar la diferencia de peso medio entre las poblaciones. Demostramos cómo hacerlo usando pruebas t e intervalos de confianza, basados en la diferencia de los promedios de las muestras. Podemos obtener los mismos resultados exactos utilizando un modelo lineal:
con el peso medio de la dieta chow, la diferencia entre las medias, cuando el ratón recibe la dieta alta en grasas (hf), cuando recibe la dieta chow, y explica las diferencias entre los ratones de la misma población.
Modelos lineales en general
Hemos visto tres ejemplos muy diferentes en los que se pueden utilizar los modelos lineales. Un modelo general que engloba todos los ejemplos anteriores es el siguiente:
Nótese que tenemos un número general de predictores . El álgebra matricial proporciona un lenguaje compacto y un marco matemático para calcular y hacer derivaciones con cualquier modelo lineal que se ajuste al marco anterior.
Estimación de parámetros
Para que los modelos anteriores sean útiles tenemos que estimar las incógnitas s. En el primer ejemplo, queremos describir un proceso físico para el que no podemos tener parámetros desconocidos. En el segundo ejemplo, entendemos mejor la herencia estimando en qué medida, en promedio, la altura del padre afecta a la altura del hijo. En el último ejemplo, queremos determinar si existe realmente una diferencia: si.
El enfoque estándar en ciencia es encontrar los valores que minimizan la distancia del modelo ajustado a los datos. Lo siguiente se denomina ecuación de mínimos cuadrados (LS) y la veremos a menudo en este capítulo:
Una vez que encontremos el mínimo, llamaremos a los valores las estimaciones de mínimos cuadrados (LSE) y los denotaremos con . La cantidad obtenida al evaluar la ecuación de mínimos cuadrados en las estimaciones se llama suma residual de cuadrados (RSS). Como todas estas cantidades dependen de , son variables aleatorias. Las s son variables aleatorias y eventualmente realizaremos inferencia sobre ellas.
Ejemplo del objeto que cae revisado
Gracias a mi profesor de física del instituto, sé que la ecuación de la trayectoria de un objeto que cae es:
con y la altura y la velocidad iniciales respectivamente. Los datos que simulamos anteriormente siguieron esta ecuación y añadieron el error de medición para simular n las observaciones de la caída de la bola desde la torre de Pisa . Por eso usamos este código para simular los datos:
g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)Aquí se ven los datos con la línea sólida que representa la verdadera trayectoria:
plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)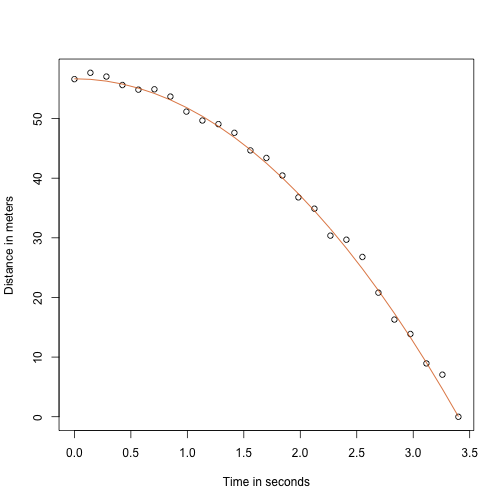
Pero estábamos simulando ser Galileo y por eso no conocemos los parámetros del modelo. Los datos sí sugieren que es una parábola, así que la modelamos como tal:
¿Cómo encontramos el LSE?
La función lm
En R podemos ajustar este modelo simplemente usando la función lm. Describiremos esta función en detalle más adelante, pero aquí hay un avance:
tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17Nos da el LSE, así como los errores estándar y los valores p.
Parte de lo que hacemos en esta sección es explicar las matemáticas que hay detrás de esta función.
La estimación por mínimos cuadrados (LSE)
Escribamos una función que calcule el RSS para cualquier vector :
rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}Así que para cualquier vector tridimensional obtenemos un RSS. Aquí tenemos un gráfico del RSS en función de cuando mantenemos los otros dos fijos:
Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)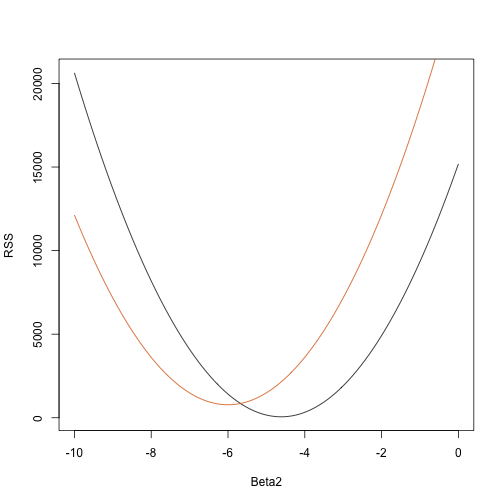
El ensayo y error aquí no va a funcionar. En su lugar, podemos utilizar el cálculo: tomar las derivadas parciales, ponerlas a 0 y resolver. Por supuesto, si tenemos muchos parámetros, estas ecuaciones pueden volverse bastante complejas. El álgebra lineal proporciona una forma compacta y general de resolver este problema.
Más sobre Galton (Avanzado)
Al estudiar los datos de padre e hijo, Galton hizo un descubrimiento fascinante utilizando el análisis exploratorio.
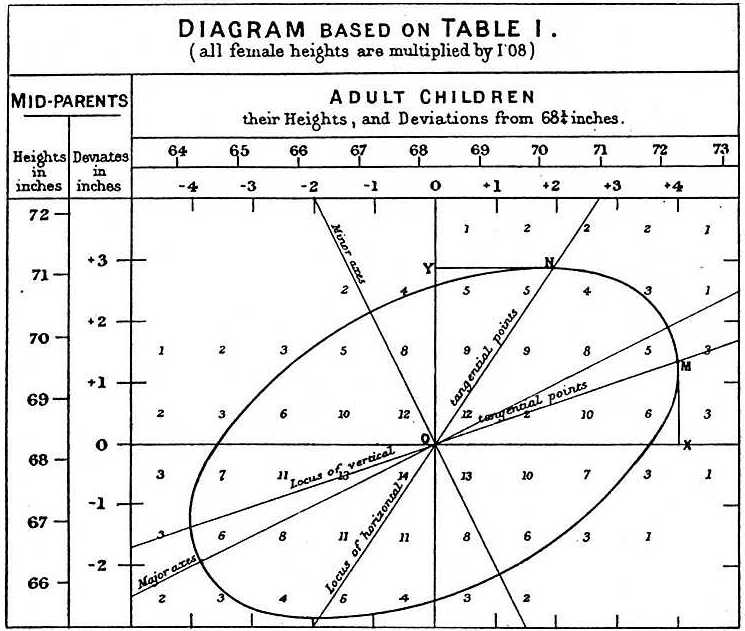
Observó que si tabulaba el número de pares de altura de padre e hijo y seguía todos los valores x,y que tenían los mismos totales en la tabla, formaban una elipsis. En el gráfico de arriba, realizado por Galton, se ve la elipsis formada por los pares que tienen 3 casos. Esto llevó entonces a modelar estos datos como normales bivariados correlacionados que describimos antes:
Describimos cómo podemos usar las matemáticas para mostrar que si se mantiene fija (la condición de ser ) la distribución de se distribuye normalmente con media: y desviación estándar . Nótese que es la correlación entre y , lo que implica que si fijamos , sigue de hecho un modelo lineal. Los parámetros y en nuestro modelo lineal simple se pueden expresar en términos de , y .