Bemærk: dette er side et af vores Vortex Math-analyse. Klik her, hvis du ledte efter den interaktive Vortex-N-k app.
Kære Professor Puzzler,
Jeg har hørt folk tale om “Vortex Math”, og jeg vil gerne forstå, hvad det er. Kan du hjælpe mig?
Mystified i Maine
Kære Mystified,
Jeg vil med glæde hjælpe dig. Dette bliver en smule teknisk til tider, men for at gøre tingene interessante har min gode ven Marko-11 fra Wunfishia tilbudt at lave et gæsteindlæg. Marko-11 er lidt mærkelig (bogstaveligt talt) – han har elleve fingre i stedet for ti, og det giver ham et helt nyt perspektiv på matematik. Hvis du bliver hængende med ham til slutningen af hans forklaring, garanterer jeg, at du vil nyde turen! Marko?
Tak, professor Puzzler. Jeg er nødt til at advare dine læsere om, at jeg kommer til at lave lidt let talteori her, men hvis matematik ikke er deres stærke side, kan de lade øjnene glide ned under det matematiske og bare kigge på min kommentar til de smukke billeder.
Jeg vil gerne starte med at sikre mig, at alle dine venner forstår, at ikke alle tæller som dem selv. De fleste af dine venner tæller sandsynligvis i et talsystem, der hedder base ti, som har følgende cifre: 0, 1, 2, 3, 4, 5, 6, 7, 8 og 9. Det er ikke usædvanligt, da de alle har ti fingre. Jeg derimod regner (så at sige) i base 11 (du kan sikkert gætte hvorfor). Mit tællesystem har et ekstra ciffer, ligesom jeg har et ekstra ciffer. Mine cifre er 0, 1, 2, 3, 4, 4, 5, 5, 6, 6, 7, 8, 9 og A. “A?” Du vil måske sige: “Det er et bogstav, ikke et tal!” Sandt, sandt, men når man arbejder i en base større end ti, har man brug for ekstra cifre, og i stedet for at opfinde nye symboler, tager vi bare symboler, der ikke bruges til andet (med undskyldning til mine venner engelsklærerne!)
Nu, fordi jeg regner i base 11, skriver jeg tal meget anderledes. Når jeg f.eks. ønsker at skrive tallet 34, skriver jeg “31”. Hvorfor? Fordi det betyder “3 elleve, plus 1 mere”. Tallet 87 skriver jeg “7A”, fordi 7 elleve plus A (det er dit tal 10) er 87.
Så jeg skal lave noget smart regning, og det hele foregår i base 11, så du skal være meget opmærksom for at følge mig.

Først tegner jeg en cirkel og markerer alle mine tal rundt om cirklen. Nå, faktisk ikke dem alle; jeg springer nul over. Spørg mig ikke hvorfor; jeg er ikke sikker på, at jeg faktisk har en god grund, men det vil få det hele til at blive rigtigt. Så stol bare på mig. Jeg har elleve fingre, så hvordan kan jeg tage fejl?
Okay, nu hvor jeg har tegnet min cirkel, vil jeg begynde at forbinde tallene i følgende mønster. Jeg starter med 2 og fordobler det. Resultatet er 4. Så jeg forbinder 2 og 4. Nu fordobler jeg 4. Det giver 8, så jeg forbinder 4 og 8. Nu fordobler jeg 8, og det er … øh åh … det er 15. (Jeg ved, hvad du tænker – det er 16. Men det er i base ti. I base elleve skrives 16 15, fordi 1 elleve plus 5 mere er 16).
Fint, men jeg har ikke et ciffer 15. Det er okay … jeg lægger bare 1 og 5 sammen til 6, og så forbinder jeg 8 og 6. Nu fordobler jeg 15 (base 11), og jeg får 2A (det er 32 for dig!). Nu lægger jeg cifrene 2 + A = 11 (base elleve) sammen. Da jeg ikke har et ciffer 11, lægger jeg cifrene sammen: 1 + 1 = 2, og så trækker jeg en linje, der forbinder 6 og 2.

Wow! Det ser virkelig fedt ud! Det ligner et smukt uendelighedssymbol, som er universets måde at fortælle mig, at jeg er i gang med noget ekstra specielt, som vil resultere i uendeligt alting for alle!
For at gøre det endnu mere interessant, hvis jeg fordobler 2A, og laver min kortlægningsproces, så kortlægger det til 4, og den næste fordobling kortlægger til 8, så 6, og det gentager sig igen og igen og igen og igen, hvilket selvfølgelig er et symbol på den uendelige rigdom, der venter mig, når jeg har solgt denne idé til andre Wunfishianere!
Men hvad med stakkels små 3, 5, 7, 9 og A? Hvad er de kortlagt til? Det er her, det bliver VIRKELIG fedt; 1 svarer til 2, 3 svarer til 6, 5 svarer til A, 7 svarer til 4 og 9 svarer til 8. Med andre ord, med undtagelse af 5, indgår de alle i uendelighedens cyklus og giver mig endnu mere af den uendelige energi, rigdom og kræftbekæmpelsespotentiale, som jeg allerede har opdaget. Hvad? Har jeg ikke fortalt dig om at bekæmpe kræft? Nå ja. Det er en selvfølge.
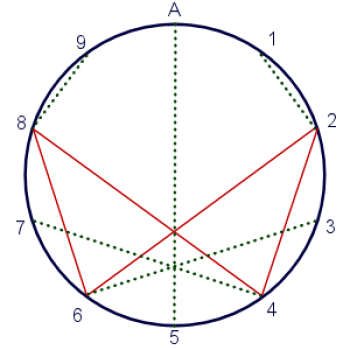
Og hvad er A kortet til? Det er det fantastiske; A kortlægger til SIG SELV. Uanset hvor mange gange man fordobler det, bliver A bare ved med at afbilde sig selv. Det fortæller mig, at A (dit tal 10) er den magiske konstant, der styrer universet og binder matematikkens guddommelige sprog sammen.
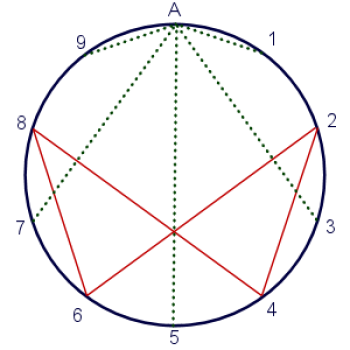
Det hele ville faktisk se meget federe ud, hvis jeg i stedet for at mappe 1, 3, 7 og 9 ind i den uendelige løkke, mappede dem ind i mit magiske tal. Spørg mig ikke hvorfor – jeg har ikke brug for en grund. Det ser bare cool ud, så det gør jeg.
Nu ligner mit vortex-diagram uendelighed under et juletræ, hvilket er universets måde at fortælle mig på, at dette er dets gave til mig.
Nej, det er det slet ikke. Ser du, jeg har ikke opfundet Vortex Matematik. Den blev opfundet af en stakkels fyr (jeg kalder ham gerne Marko-10), som desværre kun havde 10 fingre. Og fordi han kun havde 10 fingre, begik han den triste fejl at forsøge at gøre alt dette i base ti.
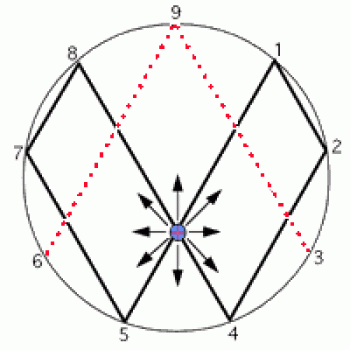
Selvfølgelig var hans vortexdiagram ikke så kønt som mit. Bemærk, at hans uendelighedssymbol er langt mindre elegant end mit, og at det kræver en ekstra fordobling for at sløjfe tilbage til den uendelige godhed. Bemærk også, at han ikke rigtig vidste, hvad han skulle gøre med stakkels lille 3 og 6, som snobbet bare kortlægger frem og tilbage til hinanden, og som ikke føder ind i hans uendelige energiforsyning.
Og har hans juletræ overhovedet en stamme? Nej, det har det ikke. Og der er kun ét sæt grene, så universet kan ikke få plads til mange gaver under det træ.
Hvad er det for en sjov pileting i midten? Det gør åbenbart det hele til et symbol på oplysning. Altså, så oplyst som man kan blive, hvis man er et ti-fingret væsen! Hvis du er oplyst nok, vil dette symbol hjælpe dig med at finde frem til Guds hemmelige navn – det er i hvert fald, hvad Marko-10 siger. Men jeg formoder, at det kan afhænge af, om Gud også kun har ti fingre eller ej. (Hvis du ikke har regnet det ud endnu, så laver Marko-10 ikke matematik; han laver baha’i-mystik.)
Oh, ja, og da Marko har ti fingre, mener han, at NIN er det magiske tal, der binder universets forenende blah-blah-blah-blah sammen, og som vil kurere kræft, give os gratis energi og måske også kurere skaldethed. Hvorfor? Fordi universet tilsyneladende faktisk bekymrer sig om, at han kun har ti fingre i stedet for elleve.
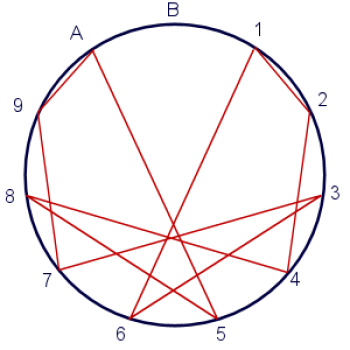
Tak for denne forklaring, Marko-11. Jeg håber, at du får en dejlig tur tilbage til Wunfishia (jeg ved godt, at der er langt herfra og dertil, og der er sjove ting overalt!). Åh, og tak fordi du præsenterede mig for din fætter fra Blufishia, Marko-12 (jeg er sikker på, at alle kan regne ud, hvorfor han hedder Marko-12). Marko-12 lavede sin egen magiske analyse af tal i base tolv. Han kom frem til et virkelig sejt vortex-diagram, der ligner en kombination af en ørn og et pentagram.
Koincidence? Jeg er sikker på, at det ikke er det. Jeg er sikker på, at det er universets måde at fortælle ham, at han vil stige til store højder, hvis han bare rækker ud efter stjernerne.
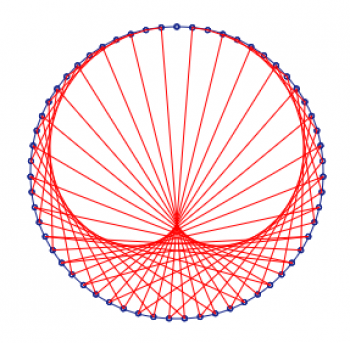
Selvfølgelig holder ikke engang Marko-12 et lys for de gamle babylonieres genialitet; hvis bare nutidens vortex-baserede “matematikere” var lige så avancerede som disse fyre, ville deres vortex-diagram have lignet dette fantastiske kunstværk! Og ja, det er virkelig en enkelt løkke, der rammer hvert enkelt ciffer i cirklen undtagen deres base-sixty-ciffer for 59. Med al respekt for Marko-10, så er FJENSTINDE-NINUNDE meget sejere end NINE!
En sidste bemærkning: VBM-folkene (Vortex Based Math) mener, at deres magiske diagram er en “guddommelig kode”, men uanset om man tror på Galileos udsagn “Matematikken er det sprog, som Gud har skrevet universet med” eller ej, kan man ikke benægte, at base ti er en fuldstændig menneskelig konstruktion. Så hvis deres diagram er “guddommeligt”, så er det også tilfældet med alle de utallige (bogstaveligt talt uendelige!) smukke diagrammer (og tilhørende storslåede mønstre!), som de ignorerer, fordi de er bundet til og fastlåst af tallet ti.
Det tog mig i alt 5 minutter at udvikle et stringent matematisk bevis for, at hvis man arbejder i base N, så har N-1 deres “magiske tal”-adfærd. Hvis de var rigtige matematikere, ville det være den slags arbejde, de kunne udføre, men de er baha’i-mystikere i stedet for matematikere, og de kan ikke se skoven på grund af deres eget sørgelige lille juletræ…
I stedet for at spilde din tid med dem, så hav det rigtig sjovt – lær at arbejde i andre baser end base ti, og skab så dine egne vortex-diagrammer. Vil de hjælpe dig med at skabe gratis energi? Eller kurere akne? Naturligvis ikke, men de er i hvert fald smukke, og de fungerer også som rigtig fine Rorchach-tests, der fortæller dig mere om dig selv end om universets natur.
Professor Puzzler
P.S. Her er en visuel hjælp til at få en smagsprøve på “vortexdiagrammer” i andre baser: Beyond Vortex Based Math