Punktsymmetri eksisterer, når figuren er tegnet omkring et enkelt punkt.

Dette punkt kaldes figurens centrum eller symmetriens centrum. I figuren ved siden af ser vi, at der svarende til punktet X på figuren findes et punkt X’ på den anden side af centrum, som er direkte modsat X og ligger på figuren. Vi siger, at figuren er symmetrisk omkring centrum.
Note:
Når vi roterer en figur omkring 180°, og den genvinder sin oprindelige form, siger vi, at der findes punktsymmetri i figuren.
Eksempler på figurer, der udviser punktsymmetri:
● Alle bogstaver i det engelske alfabet.
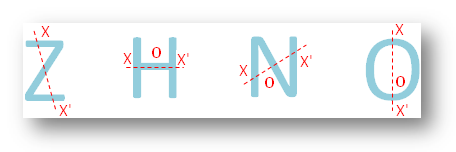
● Forskelligegeometriske figurer.
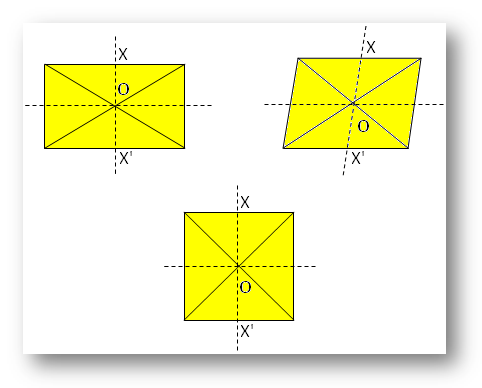
Note:
Her er O symmetriens centrum.
Med hensyn til X findes der X’, således at X’ er direkte modsat X på den anden side af O.
Hvilke betingelser opfylder en form eller en figur for punktsymmetri?
De betingelser, som en form eller en figur opfylder for punktsymmetri, dvs. at hver del skal have en tilsvarende del
– afstanden skal være ens fra det centrale punkt
– men skal være i modsat retning.
● Relaterede begreber
● Lineær symmetri
● Symmetrilinjer
● Rotationssymmetri
● Rotationssymmetriens rækkefølge
● Typer af symmetri
● Refleksion
● Refleksion af et punkt i x-akse
● Refleksion af et punkt i y-akse
● Refleksion af et punkt i y-akse
● Refleksion af et punkt i oprindelsen
● Rotation
● 90 graders rotation mod uret
● 90 graders rotation mod uret
● 180 graders rotation
● 180 graders rotation
7. klasse Matematikopgaver
8. klasse Matematikøvelse
Fra punktsymmetri til HJEMMESIDE