Hvor vi begynder, skal vi gøre nogle antagelser.
Først arbejder vi med newtonske væsker. Dette er den enkleste matematiske måde at redegøre for viskositeten i en væske på. Der findes ingen virkelige væsker, der falder helt ind under denne kategori, men i de fleste tilfælde kan luft og vand behandles som en newtonsk væske. Den anden meget vigtige hypotese, vi opstiller, er, at væsken er inkompressibel. Det betyder, at dens massefylde, rho, er en konstant.
Massebevarelse
Den første ligning fortæller os, at den masse af væsken, vi arbejder med, er bevaret. Væsken kan ændre sin form, men denne ligning fortæller os, at massen er den samme fra start til slut.
Nu skal vi tale matematik. Bogstavet u repræsenterer væskens hastighed, og det er en vektor. Det har tre komponenter, vi kan kalde dem u, v og w, og de repræsenterer væskens hastighed i x-, y- og z-retningen. Det græske bogstav nabla ∇ efterfulgt af et punktum er divergensoperatoren. Det betyder, at vi skal differentiere dens komponenter i hver retning (i dette tilfælde x, y, z).

Den første afledte fortæller os, hvordan x-komponenten af hastigheden ændrer sig, når vi bevæger os i x-retningen. Det samme gælder for de to andre afledte. Da denne ligning er lig med nul, viser den os, at massen er bevaret.
Momentbevarelse

Den anden ligning er faktisk et sæt af tre differentialligninger. Det er den, der kan beskrives som Newtons anden lov for væskerne. Hvis vi udvider udtrykket, får vi et komplekst system.
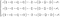
Da det er meget mere enkelt at forstå, vil vi koncentrere os om den ikke udvidede momentbevarelse.
Når vi arbejder med væsker kan vi sige, at masse og massefylde er de samme ting (så længe deres volumen er det samme). Hvis vi betragter to væsker, kan vi sige, at den tættere af dem er den “tungere” (f.eks. kviksølv og vand). I dette tilfælde er det græske bogstav ρ (rho) væskens massefylde.
Vi har massen, og for at vende tilbage til Newtons anden lov skal vi nu bruge accelerationen. Det er netop resultatet af den tidsafledte af hastighedsvektoren.

Nu har vi kun termerne på højre side af lighedstegnet tilbage, og de repræsenterer alle de kræfter, der påføres væsken.
Den første term ∇p er gradienten af trykket. Det repræsenterer forskellen i trykket i det rum, hvor væsken befinder sig. Hvis der f.eks. er en zone med lavt tryk og en anden med et højere tryk, vil væsken bevæge sig fra højtryksområdet til det lavere område. Gradienten af p siger alt dette.
Den anden term beskriver væskens viskositet. Tænk på to forskellige væsker, f.eks. vand og honning. Når du hælder et glas vand op, falder det hurtigt og let. Når du gør det samme med honning, er det klistret, og det hældes meget langsomt. Det er det, som dette udtryk siger.
Det sidste udtryk, F, er det letteste, fordi det repræsenterer alle de ydre kræfter, der kan påføres denne væske. Normalt er den kraft, vi betragter her, tyngdekraften.
Det er det, alle disse smarte symboler og bogstaver betyder er bare kraft = masse x acceleration.
Anvendelse af Navier-Stokes-ligningerne
Da det er så kompliceret at løse disse ligninger, er vi nødt til at foretage en masse tilnærmelser for at bruge dem. Nogle eksempler er Poiseuille- og Couette-strømningen. Med en masse antagelser var disse to videnskabsmænd i stand til at finde en løsning på Navier-Stokes-ligningerne til en meget specifik anvendelse. Men hvis vi ønsker at bruge dem til en mere kompliceret opgave, som f.eks. vejrudsigter, skal vi gøre noget andet.
Den mest almindelige måde at bruge disse ligninger på er ved at transformere dem, med Reynoldsgennemsnittet. Dette er en avanceret matematisk proces, og resultatet er Reynoldsligningerne. De kaldes normalt RANS-ligninger (hvilket betyder Reynolds averageed Navier-Stokes).
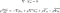
Disse ligninger anvendes, når væsken befinder sig i en turbulent strømning. De ligner næsten nøjagtigt Navier-Stokes-ligningerne, bortset fra det sidste udtryk. Dette kaldes Reynolds stress tensor. Det er den størrelse, der gør det muligt at tage højde for turbulensen i væsken.
I RANS-ligningerne er de størrelser, vi bruger, middelværdien af de mængder, vi bruger, beregnet over et tidsinterval. Dette interval skal være lille nok til, at det er muligt at observere det fænomen, vi studerer. Samtidig skal det være stort nok til, at turbulensvirkningen mister betydning.
Med de rigtige forudsætninger fungerer disse ligninger. Vi ved, hvordan vi kan bruge dem til at gøre F1-biler hurtigere, til at få et rumfartøj til at flyve til ISS og til at lave vejrudsigter. Så du undrer dig måske over, hvorfor beviset for disse ligninger er en million dollars værd?
En million dollars-pris
Fra et fysisk synspunkt er disse ligninger blot Newtons anden lov, der fungerer med væsker. Når vi foretager nogle antagelser og nogle forenklinger, kan vi gøre fantastiske ting med dem.
Det virkelige problem er dette. At løse disse ligninger uden tilnærmelser er bare frygtelig kompliceret. Det er så vanskeligt, at det ikke er blevet bevist, at løsningerne faktisk findes. Og det er her, millenniumprisen kommer ind i billedet.
Den officielle problemformulering (find den her) er:
Bevis eller giv et modeksempel på følgende udsagn: I tre rumdimensioner og tid findes der, givet et indledende hastighedsfelt, en vektorhastighed og et skalært trykfelt, som begge er glatte og globalt definerede, og som løser Navier-Stokes-ligningerne.
Det betyder, at for at vinde prisen skal man gøre tre ting:
- Bevise, at der findes en løsning
- Løsningen skal eksistere i hvert punkt i rummet
- Løsningen skal være glat. Det betyder, at en lille ændring i de indledende betingelser kun giver en lille variation i resultatet.
For en ingeniør er det normalt nok at vide, at disse ligninger virker, om end kun til en vis grad af tilnærmelse. Men for en matematiker er det meget vigtigt at vide, om løsningerne findes, og hvordan de opfører sig.
Du tænker måske nu, at hvis de virker, som de gør, er det totalt spild af tid og energi at bruge tid og energi på at søge efter et bevis. Tja, som mange teknologiske fremskridt i menneskehedens historie kan resultatet måske ikke synes særlig vigtigt. Det vigtige er vejen dertil, som kan bringe ny viden og forbedringer til vores liv.
Tænk på rummissioner. Hvis mennesket aldrig havde besluttet sig for at tage ud og gå på månen, ville vi ikke have mange genstande, der bruges til at forbedre vores liv. MRI-maskiner og pacemakere kommer fra teknologier, der er udviklet til rumforskning. I dag bruger læger over hele verden dem hver dag til at redde liv. Det samme gælder her. Vejen til at finde løsningen på Navier-Stokes-ligningerne vil hjælpe os til at forbedre vores forståelse af væsker og meget mere. Det kan føre os til nye opdagelser og vil sandsynligvis kræve, at vi opfinder ny matematik. Dette kan så bruges til at løse mange andre problemer og til at opfinde nye teknologier, der kan forbedre vores liv og gøre os bedre.