Vi vil beskrive tre eksempler fra biovidenskaberne: et fra fysik, et fra genetik og et fra et museksperiment. De er meget forskellige, men alligevel ender vi med at bruge den samme statistiske teknik: tilpasning af lineære modeller. Lineære modeller undervises og beskrives typisk i matrixalgebraens sprog.
Motiverende eksempler
Faldende genstande
Forestil dig, at du er Galilei i det 16. århundrede, der forsøger at beskrive hastigheden af en faldende genstand. En assistent klatrer op i Pisa-tårnet og lader en kugle falde, mens flere andre assistenter registrerer positionen på forskellige tidspunkter. Lad os simulere nogle data ved hjælp af de ligninger, vi kender i dag, og tilføje nogle målefejl:
set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##metersAssistenterne afleverer dataene til Galileo, og dette er, hvad han ser:
mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")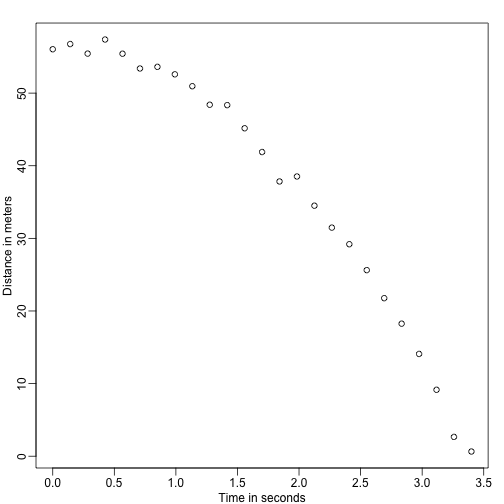
Han kender ikke den nøjagtige ligning, men ved at se på plottet ovenfor udleder han, at positionen bør følge en parabel. Så han modellerer dataene med:
Med repræsenterer positionen, repræsenterer tiden og tager højde for målefejl. Dette er en lineær model, fordi det er en lineær kombination af kendte størrelser (th s), der betegnes som prædiktorer eller kovariater, og ukendte parametre (s).
Fader & sønnens højde
Forestil dig nu, at du er Francis Galton i det 19. århundrede, og du indsamler parvise højdeoplysninger fra fædre og sønner. Du har mistanke om, at højde er arvelig. Dine data:
library(UsingR)x=father.son$fheighty=father.son$sheightser således ud:
plot(x,y,xlab="Father's height",ylab="Son's height")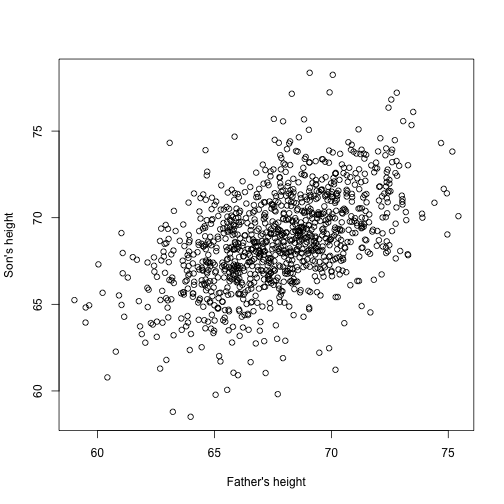
Sønnernes højde ser ud til at stige lineært med fædrenes højde. I dette tilfælde er en model, der beskriver dataene, som følger:
Det er også en lineær model med og , henholdsvis faderens og sønnens højde for det -te par og et udtryk for den ekstra variabilitet. Her tænker vi på fædrenes højder som prædiktor og som værende faste (ikke tilfældige), så vi bruger små bogstaver. Målefejl alene kan ikke forklare al den variabilitet, der ses i . Dette giver mening, da der er andre variabler, der ikke er med i modellen, f.eks. mødrenes højde, genetisk tilfældighed og miljøfaktorer.
Stikprøver fra flere populationer
Her læser vi data om musekropsvægt fra mus, der blev fodret med to forskellige diæter: fedtholdig og kontrol (chow). Vi har en tilfældig stikprøve på 12 mus for hver. Vi er interesseret i at fastslå, om kosten har en effekt på vægten. Her er dataene:
dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")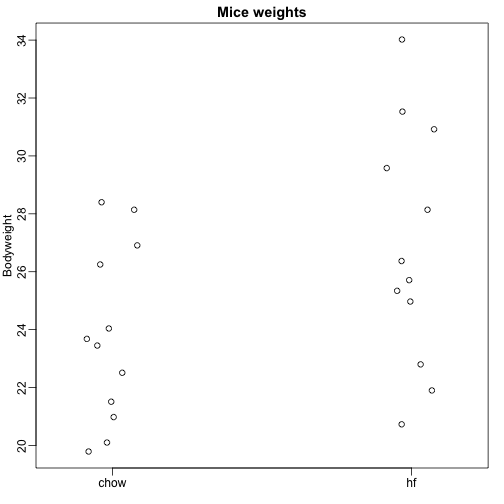
Vi ønsker at estimere forskellen i den gennemsnitlige vægt mellem populationerne. Vi demonstrerede, hvordan vi kan gøre dette ved hjælp af t-test og konfidensintervaller, baseret på forskellen i stikprøvens gennemsnit. Vi kan opnå nøjagtig de samme resultater ved hjælp af en lineær model:
med chow-kostens gennemsnitsvægt, forskellen mellem gennemsnittene, når musen får fedtholdig (hf) kost, når den får chow-kost, og forklarer forskellene mellem musene i samme population.
Lineære modeller generelt
Vi har set tre meget forskellige eksempler, hvor lineære modeller kan anvendes. En generel model, der omfatter alle de ovenstående eksempler, er følgende:
Bemærk, at vi har et generelt antal prædiktorer . Matrixalgebra giver et kompakt sprog og en matematisk ramme til at beregne og lave afledninger med enhver lineær model, der passer ind i ovenstående ramme.
Stimulering af parametre
For at ovenstående modeller kan være brugbare, er vi nødt til at estimere de ukendte s. I det første eksempel ønsker vi at beskrive en fysisk proces, hvor vi ikke kan have ukendte parametre. I det andet eksempel vil vi bedre forstå arv ved at estimere, hvor meget faderens højde i gennemsnit påvirker sønnens højde. I det sidste eksempel ønsker vi at afgøre, om der rent faktisk er en forskel: hvis .
Standardmetoden i videnskaben er at finde de værdier, der minimerer den tilpassede models afstand til dataene. Følgende kaldes ligningen for de mindste kvadrater (LS), og vi vil se den ofte i dette kapitel:
Når vi har fundet minimumsværdien, kalder vi værdierne for de mindste kvadraters estimater (LSE) og betegner dem med . Den størrelse, der fremkommer ved evaluering af mindste kvadratligningen ved estimaterne, kaldes residual sum of squares (RSS). Da alle disse størrelser afhænger af , er de tilfældige variabler. s er tilfældige variabler, og vi vil i sidste ende udføre inferens på dem.
Eksemplet med faldende objekt genoptaget
Takket være min fysiklærer i gymnasiet ved jeg, at ligningen for banen for et faldende objekt er:
med og henholdsvis starthøjden og -hastigheden. De data, vi simulerede ovenfor, fulgte denne ligning og tilføjede målefejl for at simulere n observationer for at lade bolden falde ned fra Pisa-tårnet . Derfor brugte vi denne kode til at simulere data:
g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)Her er, hvordan dataene ser ud med den gennemgående linje, der repræsenterer den sande bane:
plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)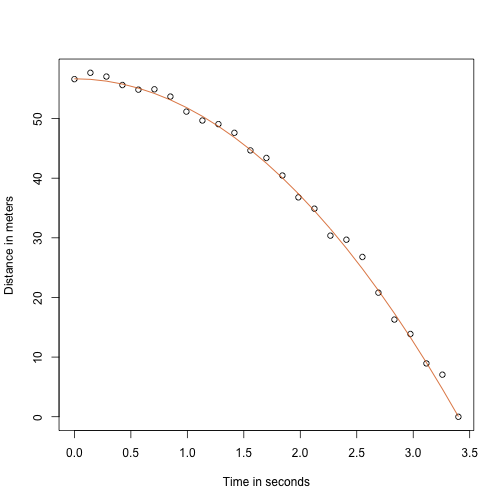
Men vi lod som om, vi var Galileo, og derfor kender vi ikke parametrene i modellen. Dataene tyder på, at det er en parabel, så vi modellerer den som sådan:
Hvordan finder vi LSE?
Den lm funktion
I R kan vi tilpasse denne model ved blot at bruge lm funktionen. Vi vil beskrive denne funktion i detaljer senere, men her er en forsmag:
tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17Den giver os LSE samt standardfejl og p-værdier.
En del af det, vi gør i dette afsnit, er at forklare matematikken bag denne funktion.
Det mindste kvadraters estimat (LSE)
Lad os skrive en funktion, der beregner RSS for en hvilken som helst vektor :
rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}Så for en hvilken som helst tredimensionel vektor får vi en RSS. Her er et plot af RSS som en funktion af, hvornår vi holder de to andre fast:
Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)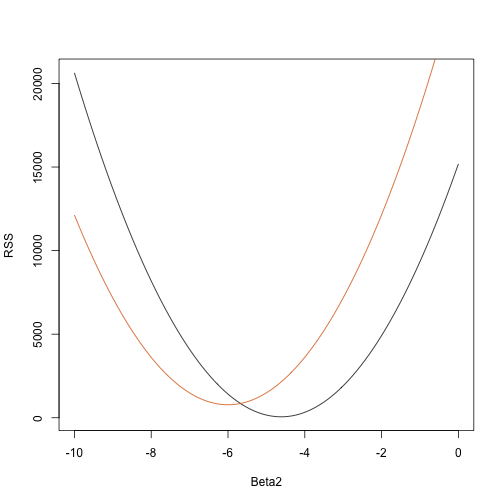
Trial and error her kommer ikke til at virke. I stedet kan vi bruge regning: Tag de partielle afledninger, sæt dem til 0 og løs dem. Hvis vi har mange parametre, kan disse ligninger naturligvis blive ret komplekse. Lineær algebra giver en kompakt og generel måde at løse dette problem på.
Mere om Galton (Avanceret)
Når han studerede far-søn-dataene, gjorde Galton en fascinerende opdagelse ved hjælp af eksplorativ analyse.
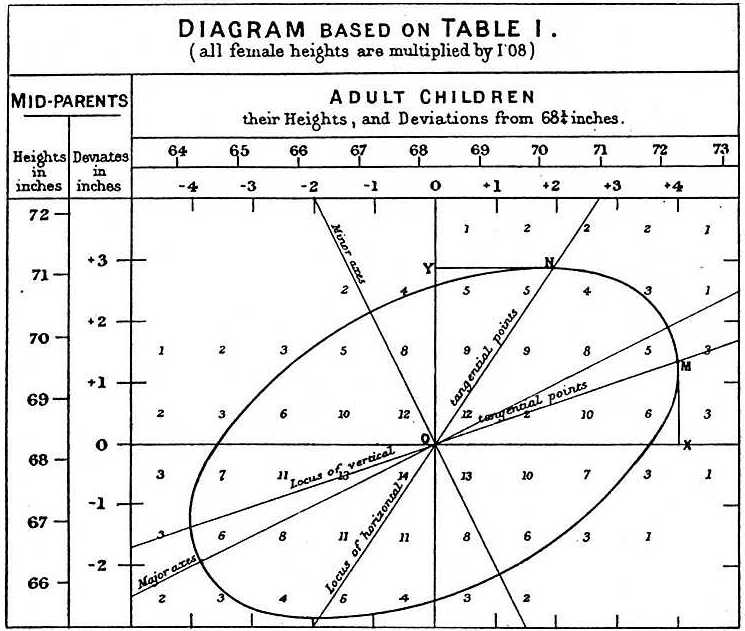
Han bemærkede, at hvis han tabulerede antallet af far-søn-højdepar og fulgte alle de x,y-værdier, der havde de samme totaler i tabellen, dannede de en ellipse. I ovenstående plot, som er lavet af Galton, ser man ellipsen dannet af de par, der har 3 tilfælde. Dette førte så til at modellere disse data som korreleret bivariat normal, som vi beskrev tidligere:
Vi beskrev, hvordan vi kan bruge matematik til at vise, at hvis man holder fast (betingelse til at være ) er fordelingen af normalt fordelt med middelværdi: og standardafvigelse . Bemærk, at er korrelationen mellem og , hvilket indebærer, at hvis vi fixer , følger faktisk en lineær model. Parametrene og i vores simple lineære model kan udtrykkes i form af , og .