 |
Ligebenet trekant |
|
Vi skal lave TRE konstruktioner af en ligesidet trekant. Den første vil være at konstruere en ligesidet trekant ud fra længden af den ene side, og de to andre vil være at konstruere en ligesidet trekant, der er indskrevet i en cirkel.
|
Givet: længden af den ene side af trekanten
Konstruer: en ligesidet trekant |
 |
Trin:
1. Placer kompaspunktet på A, og mål afstanden til punkt B. Sving en bue af denne størrelse over (eller under) segmentet.
2. Uden at ændre spændvidden på kompasset placerer du kompaspunktet på B og svinger den samme bue, der skærer den første bue.
3. Mærk skæringspunktet som det tredje toppunkt i den ligesidede trekant.
 |
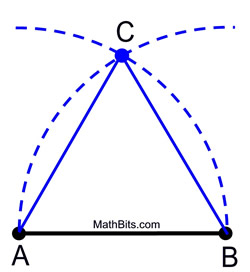Se fuldcirklerne i arbejde.
 |
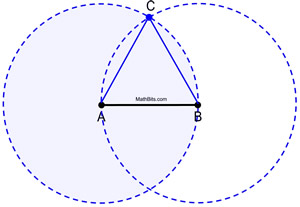Bevis for konstruktionen: Cirkel A er kongruent med cirkel B, da de begge er dannet med den samme radiuslængde, AB. Da AB og AC er længder af radiuslængder af cirkel A, er de lig hinanden. På samme måde er AB og BC radiuslængder af cirkel B, og de er lig hinanden. Derfor er AB = AC = BC ved substitution (eller transitiv egenskab). Da kongruente segmenter har samme længde, 
og ΔABC er ligesidet (har tre kongruente sider).
|
Givet: et stykke papir
Konstruer: en ligesidet trekant, der er indskrevet i en cirkel. |
Dette er en modifikation af konstruktionen af en regelmæssig sekskant indskrevet i en cirkel.
|
Trin:
1. Placer din kompaspunkt på papiret, og tegn en cirkel. (Behold dette kompasspænd!)
2. Placer en prik, mærket A, et vilkårligt sted på cirklens omkreds som startpunkt.
3. Uden at ændre kompasets spændvidde placerer du kompaspunktet på A og svinger en lille bue, der krydser cirklens omkreds.
4. Uden at ændre kompasets spændvidde flytter du kompaspunktet til skæringspunktet mellem den foregående bue og omkredsen og laver endnu en lille bue på cirklens omkreds.
5. Bliv ved med at gentage denne proces med at “træde” rundt i cirklen, indtil du vender tilbage til punkt A.
6. Med udgangspunkt i A forbinder du hver anden cirkelbue på cirklen for at danne den ligesidede trekant.
 |
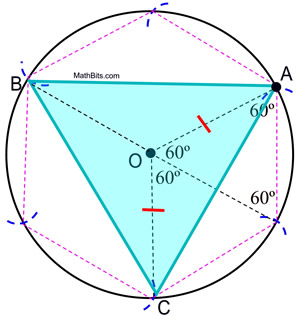Se beviset for en indskrevet regelmæssig sekskant for flere oplysninger vedrørende beviset for denne konstruktion.
|
Bevis for konstruktionen: Beviset for den indskrevne regelmæssige sekskant viser, at de centrale vinkler i en regelmæssig sekskant indeholder 60º. De centrale vinkler i den trekant, der er indskrevet i denne cirkel, indeholder 120º. Da ΔAOC er ligebenet (OA og OC er radiuslængder), er m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC 
ΔCOB ΔBOA ved SAS. Ved CPCTC er ∠OCB ∠OCA og m∠OCB = 30º ved substitution og m∠BCA = 60º. På tilsvarende måde har vi m∠ACB = m∠CBA = m∠CBA = m∠BAC = 60º og ligesidet ΔABC.
|
Givet: et stykke papir
Konstruer: en ligesidet trekant indskrevet i en cirkel. |
Denne metode anvender viden om den specielle retvinklede trekant 30º – 60º – 90º.
|
TRIN:
1. Placér dit kompaspunkt på papiret, og tegn en cirkel, O. (Behold dette kompas spændvidde!)
2. Ved hjælp af et lineal tegner du en diameter af cirklen og mærker endepunkterne P og B.
3. Uden at ændre kompassets spændvidde placerer du kompaspunktet på P og tegner en hel cirkel.
4. Mærk skæringspunkterne mellem de to cirkelomkredse med A og C.
5. Tegn segmenter fra A til B, B til C og C til A, så de danner den ligesidede trekant.
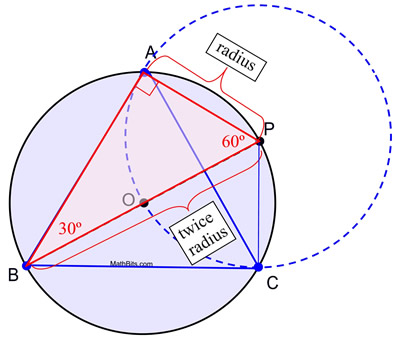
Bevis for konstruktionen: Denne konstruktion bruger det faktum, at en vinkel, der er indskrevet i en halvcirkel, er en ret vinkel, og at i en 30º-60º-90º trekant er længden af det korte ben halvdelen af længden af hypotenusen. I denne konstruktion er cirkel O og cirkel P kongruente, da de har samme radiuslængde. AP er en radiuslængde af cirkel P, og radius AP = OP. OP er også en radiuslængde af cirkel O (sammen med OB), og diameter BP = BO + OP = 2 OP. Ved substitution er BP = 2 AP, hvilket skaber de nødvendige betingelser for, at m∠ABP = 30º. Følgelig er m∠APB = 60º. Et lignende argument kan bruges til at fastslå, at for ΔPBC er m∠PBC = 30º og m∠BPC = 60º, hvilket gør ΔPBC ΔPBA ved ASA (med fælles side fra B til P).
Nu er 
, da det er de tilsvarende sider i de to kongruente trekanter, hvilket gør ΔABC ligebenet. ∠BAC ∠∠BCA, da grundvinklerne i en ligebenet trekant er kongruente.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º ved vinkeladditionspostulat og substitution. m∠BAC + m∠BCA + m∠ABC = 180º, fordi summen af vinkelmålene i en trekant er 180º. Da m∠BAC + m∠BAC + m∠BAC + 60º = 180º ved substitution, ved vi, at 2m∠BAC = 120º og m∠BAC = 60º. Følgelig er m∠BCA også lig med 60º ved substitution, hvilket gør ΔABC ligesidet.
