Indledning af Klein-flasken

Hvis du kan lide at drikke, så er en Klein-flaske ikke en anbefalet beholder. Den ligner måske nok vagt en flaske, men den omslutter ikke noget volumen, hvilket betyder, at den faktisk ikke kan indeholde nogen væske. Uanset hvad du hælder “i” vil det bare komme ud igen.

Hvordan konstruerer man sådan en mærkelig ting, og hvorfor vil man konstruere den? Matematikeren Felix Klein, der opdagede flasken i 1882, beskrev den som en overflade, der “kan visualiseres ved at vende et stykke af et gummirør om og lade det passere gennem sig selv, så ydersiden og indersiden mødes”.

Din browser understøtter ikke video-tagget.Direkte link

Det er indlysende, at Klein-flasken, ligesom den mere velkendte kugle, er en lukket overflade: den er endelig i den forstand, at man kan få plads til den i et begrænset område af rummet, men en myre kunne gå rundt på den i al evighed uden nogensinde at støde på en grænse eller falde over en kant. I modsætning til kuglen, som har en indvendig og en udvendig side, er Klein-flasken ensidig: ved at gå rundt kan vores myre nå begge sider af hvert punkt på overfladen. Dette er grunden til, at flasken ikke omslutter noget volumen, og det besvarer også “hvorfor”-spørgsmålet: Klein-flasken er interessant, fordi vi ikke støder på mange ensidige former i naturen. (Se her for et andet meget smukt billede af en Klein-flaske.)

Möbius-båndet er ensidigt – se den animerede version. (Billede og animation af Konrad Polthier.)

Hvis dette er lidt forvirrende, så tænk på et mere simpelt eksempel på en ensidig overflade: den berømte Möbius-stribe. Man kan lave en sådan ved at tage to ender af en papirstrimmel, give strimlen en drejning og derefter lime enderne sammen. Ved at bruge en papirstrimmel, hvis to sider har forskellige farver, f.eks. grøn og orange, er det let at overbevise sig selv om, at den resulterende Möbiusstrimmel er ensidig. Når du har vredet og limet, vil du opdage, at du kan nå hvert orange punkt fra hvert grønt punkt uden at skulle gennembore papiret eller klatre over dets kant.

I modsætning til Klein-flasken har Möbius-båndet en afgrænsning – den består af de to ikke-limete kanter af den oprindelige strimmel. Men der er en forbindelse mellem de to. Hvis man tager to Möbius-strimler og skaber en lukket form ved at forbinde deres grænser ved hjælp af en almindelig tosidet strimmel, som vist nedenfor, er det, man får, præcis Klein-flasken.

Din browser understøtter ikke video-tagget.Direkte link

Dette faktum inspirerede matematikeren Leo Moser til at komponere en limerick:

En matematiker ved navn KleinTænkte, at Möbiusbåndet var guddommeligt.Sagde han: “Hvis du limer kanterne af to sammen, får du en mærkelig flaske som min.”

Nogle matematikere har virkelig mange talenter!

Et andet mærkeligt træk ved Klein-flasken er, at den skærer sig selv, hvilket betyder, at det er svært at lave den af et enkelt gummirør, som Klein foreslog. Strengt taget er det selvskærende objekt, der er afbildet ovenfor, ikke en Klein-flaske, men (som Klein angav) kun en visualisering af en sådan. For at forstå hvorfor, skal man først tænke på den mere velkendte doughnut (matematisk kendt som en torus). Man kan lave en torus af en firkantet gummiplade ved først at lime to modsatte sider sammen til en cylinder og derefter lime de to grænsedele af denne cylinder sammen for at få torus.

Fremstilling af en torus: Først limes modsatte punkter på to modsatte sider af kvadratet for at lave en cylinder, og derefter limes de to grænsekredse af denne cylinder (svarende til limning af modsatte punkter på de resterende to sider af kvadratet) for at danne en torus.

Hvis du ikke vil gide at gide at lime, kan du blot tænke på torus som en firkant, idet du skal huske, at modsatte punkter på modsatte sider betragtes som det samme. Så når du skubber en form, der er tegnet på “kvadratet”, hen over den øverste kant, vil den dukke op igen ved den nederste kant, og når du skubber den hen over den højre kant, vil den dukke op igen ved den venstre kant (og omvendt).

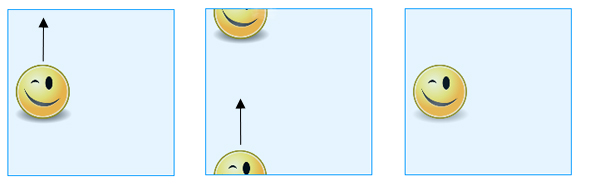
Når du skubber en form, der er tegnet på “kvadratet”, over den øverste kant, vil den dukke op igen ved den nederste kant.

For at få en ægte Klein-flaske skal du starte på samme måde og identificere modsatte punkter på et par modsatte sider af et kvadrat. For det andet par sider skal du dog ikke identificere punkter, der er direkte modsatrettede, men punkter, der er diagonalt modsatrettede, som vist på billedet.

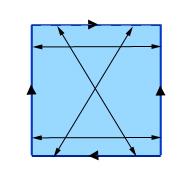
Byg en Klein-flaske: Identificer modsatte punkter på to modsatte sider (de lodrette på dette billede) og identificer derefter diagonalt modsatte punkter på de resterende to sider. (Hvis du mærker punkterne på over- og undersiden fra venstre mod højre med tallene 0 til 1, så identificeres et punkt med mærket x på oversiden med punktet med mærket 1-x på undersiden.)

Det resulterende objekt er Klein-flasken. Igen kan man tænke på den som et kvadrat, idet man skal huske, hvilke grænsepunkter der betragtes som ens. Hvis du skubber en form hen over en af de kanter, hvor der er identificeret modsatte punkter (lodret i vores billede), vises den igen igen på den modsatte side, som før. Hvis du derimod skubber den over en af de kanter, hvis punkter blev identificeret diagonalt (vandret i vores billede), vises den på den modsatte side, men forskudt og som et spejlbillede af sit oprindelige selv.

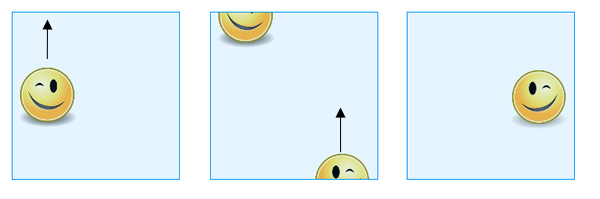
Hvis man skubber en form over den øverste kant, vises den på tværs af den nederste kant, men over på den anden side og som et spejlbillede af sit oprindelige selv.

Den eneste måde at opbygge denne form i det tredimensionelle rum på ved faktisk at lime punkter sammen er at lade den skære sig selv. Dette svarer til at identificere punktpar i det indre af det oprindelige kvadrat, så strengt taget er den resulterende form ikke nøjagtig den samme som Klein-flasken, hvor der kun er identificeret grænsepunkter. Det er blot en måde at repræsentere flasken i det tredimensionelle rum på (der findes også andre).

Mærkeligt nok afhænger begreberne “inde”, “ude” og “ensidighed” af det omgivende rum, som et objekt befinder sig i. F.eks. har en løkke tegnet på et stykke papir (i det todimensionelle rum) en veldefineret inderside og yderside, men det har en løkke tegnet i det tredimensionelle rum ikke. Derfor kan vi ikke tale om ensidighed, medmindre vi først beslutter os for, hvordan en overflade skal indlejres i det tredimensionelle rum. Der findes imidlertid en nært beslægtet egenskab, som er iboende for en form og ikke afhænger af det omgivende rum. En overflade kaldes orienterbar, hvis man ikke kan skubbe en form, der er tegnet på den, rundt og tilbage til det sted, hvor den startede, så den ligner sit eget spejlbillede. Som du kan se i den animation, der ledsager billedet til højre, er Möbiusstriben ikke orienterbar. Og som du kan se på billedet med smiley’en ovenfor ovenfor, er Klein-flasken det heller ikke. for at give den sin fulde matematiske beskrivelse, er Klein-flasken en lukket, ikke-orienterbar overflade. Hvis du vil vide mere om den, kan du se artiklen Inside the Klein bottle.

Om forfatteren

Marianne Freiberger er redaktør for Plus.