Hvad er cellemembranens permeabilitet?
Reader Mode
Et af de karakteristiske kendetegn ved alle levende organismer er, at de indeholder en karakteristisk blanding af ioner og små molekyler. Sammensætningen adskiller sig ikke kun fra omgivelserne, men kan også variere inden for cellen. F.eks. kan koncentrationen af hydrogenioner i nogle cellekompartmenter være 104 gange større end i andre (mitokondrierne når en pH på helt op til 8; lysosomerne med en pH på helt ned til 4, BNID 107521, 106074). Forholdet mellem koncentrationerne af Ca2+-ioner i de ekstra- og intracellulære væskekompartmenter kan igen være 104 gange større (BNID 104083). Denne koncentrationsforskel er så stor, at transport af en Ca2+-ion gennem membranen fra det intra- til det ekstracellulære kompartment kræver energi fra mere end én proton eller natriumion, der strømmer ned ad proton-motivationskraftgradienten. For at se dette bør læseren huske tommelfingerreglen fra vores liste over tricks of the trade, som siger, at det kræver 6 kJ/mol (≈2 kBT) at etablere en størrelsesorden af potentialforskel. Denne energi kan f.eks. opnås ved transport af én elektrisk ladning gennem en 60 mV potentialforskel. For at opnå et koncentrationsforhold på fire størrelsesordener ville det så kræve, at en ladning transporteres ned omkring 240 mV elektronmotivationskraft (faktisk endnu mere på grund af calciumionens dobbelte ladning). Dette er meget tæt på membranens nedbrydningsspænding som omtalt i vignetten om “Hvad er den elektriske potentialforskel på tværs af membraner?”. Faktisk opnås det høje koncentrationsforhold af Ca2+ normalt ved kobling til transport af tre natriumioner eller hydrolyse af ATP, hvilket bidrager til at opnå den krævede tæthedsforskel uden farlig energitilførsel til membranen.
Termodynamikkens anden lov lærer os, at tilstedeværelsen af koncentrationsgradienter generelt til sidst vil blive afblæst af massetransportprocesser, som støt og roligt driver systemer til en ligevægtstilstand. Men selv om termodynamikkens anden lov fortæller os arten af den endelige tilstand i et system (f.eks. ensartede koncentrationer), fortæller den os ikke, hvor lang tid det vil tage at opnå denne tilstand. Membraner har udviklet sig til at udgøre en meget effektiv barriere for den spontane overførsel af mange ioniske og molekylære arter. For at vurdere tidsskalaen for udligning af koncentrationer skal vi kende massetransporthastighederne, som afhænger af vigtige materialeegenskaber som f.eks. diffusionskonstanter og permeabiliteter.
En enormt succesfuld klasse af “love”, som beskriver opførslen af systemer, der har lidt en lille afvigelse fra ligevægt, er de lineære transportlove. Disse love forudsætter en simpel lineær sammenhæng mellem transporthastigheden for en bestemt mængde af interesse og den tilhørende drivkraft. For massetransport er der en lineær sammenhæng mellem fluxen (dvs. antallet af molekyler, der krydser en arealenhed pr. tidsenhed) og koncentrationsforskellen (der fungerer som den relevante drivkraft). For transport gennem membraner er disse idéer blevet kodificeret i den enkle ligning (for neutrale opløste stoffer) j= – p-(cin-cout), hvor j er nettoflowet ind i cellen, cin og cout henviser til koncentrationerne på indersiden og ydersiden af det membranbundne område, og p er en materialeparameter, der kaldes permeabilitet. Enhederne for p kan udledes ved at bemærke, at fluxen har enhederne antal/(areal x tid), og at koncentrationen har enhederne antal/volumen, hvilket indebærer, at enhederne for p selv er længde/tid. Ligesom mange transportmængder (f.eks. materialers elektriske ledningsevne, der spænder over 30 størrelsesordener) har permeabiliteten et meget stort dynamisk område, som illustreret i figur 1. Som det fremgår af figuren, har lipidbilayers et næsten 1010 gange større permeabilitetsområde.
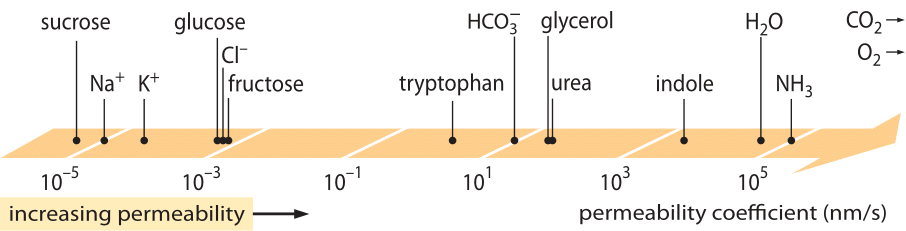
Figur 1: Det store område af membranpermeabiliteter for forskellige forbindelser i cellen. Membraner er mere permeable for uladede forbindelser og mindst permeable for ladede ioner. Bemærk, at eksistensen af ionkanaler vil gøre den tilsyneladende permeabilitet, når de er åbne, flere størrelsesordener højere. Enhederne er valgt som nm/s, og flere nm er den karakteristiske membranbredde. Figuren er tilpasset fra R. N. Robertson, The Lively Membranes, Cambridge University Press, 1983. Værdien for glukose er mindre end i Robertson baseret på flere kilder, f.eks. BNID 110830, 110807. Andre kilder til data: BNID 110729, 110731, 110816, 110824, 110806.
Hvilke fysisk-kemiske parametre styrer placeringen af en forbindelse på denne skala af permeabiliteter? En tommelfingerregel er, at små molekyler har højere permeabiliteter end større molekyler. En anden tommelfingerregel er, at neutrale forbindelser kan krydse membranen mange størrelsesordener hurtigere end tilsvarende ladede forbindelser. Blandt de ladede forbindelser har negative (anioniske) forbindelser tendens til at have meget højere permeabiliteter end positive (kationiske) forbindelser. Den såkaldte Overton-regel siger, at membranpermeabiliteten stiger med hydrofobiciteten, hvor hydrofobiciteten er en forbindelses tendens til at foretrække et ikke-polært opløsningsmiddel frem for et polært (vandigt) opløsningsmiddel. Overton-reglen forudsiger, at ladede molekyler (ikke-hydrofobiske) som f.eks. ioner vil have en tendens til at have en lav permeabilitet, da de pådrager sig en energimæssig straf ved at trænge igennem membranen, mens opløste gasser som O2 og CO2, der er hydrofobiske (da de er uladede og symmetriske), vil have en høj permeabilitet. Faktisk giver lipid-dobbeltlagsmembraners permeabilitet for CO2 værdier på 0,01-1 cm/s (ja, permeabilitetsmålinger har meget store usikkerheder blandt forskellige laboratorier, BNID 110004, 110617, 102624), hvilket er højere end alle andre værdier, der er vist i figur 1. Denne værdi viser, at den barriere, der skabes af cellemembranen, faktisk er en mindre hindring end den barriere, der skyldes det uoprørte vandlag, som opsluger cellemembranen udefra. En sådan slutning kan udledes af ligningen for permeabilitetskoefficienten for en hindring, der er givet ved p=K x D/l, hvor l er bredden, D diffusionskoefficienten og K fordelingskoefficienten mellem mediet og hindringsmaterialet. Dette er også kendt som “opløseligheds-diffusions”-modellen for permeabilitet, hvor disse betegnelser angiver K- og D-effekten, som er to trin, der påvirker permeabiliteten. For et uoprørt vandlag er K=1, da det ligner mediet meget, men for membraner er værdien for alle undtagen det mest hydrofobiske materiale normalt flere størrelsesordener mindre end 1. Denne afhængighed af K er kernen i den ovenfor nævnte Overton-regel. Den høje permeabilitet for CO2 tyder også på, at kanaler som f.eks. aquaporiner, der blev foreslået til at tjene til gastransport ind i cellen, ikke er nødvendige, da membranen er permeabel nok. For at se, hvordan membranegenskaberne påvirker den kemiske sammensætning af metabolitter, vender vi os til at beregne lækagetiden for forskellige forbindelser
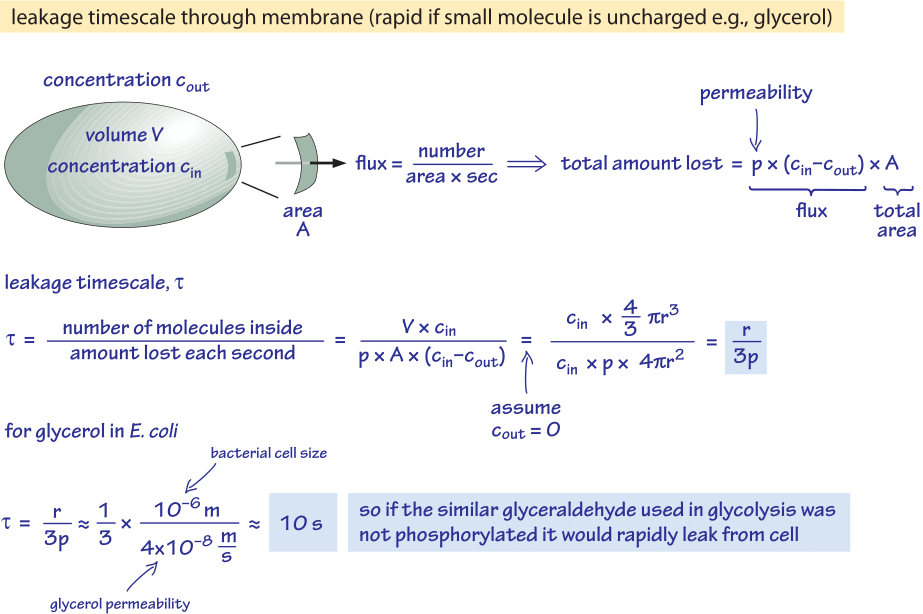
Figur 2: Back of the envelope-beregning af tidsskalaen for et ikke-fosforyleret glukosemolekyle til passivt at diffundere ud af en bakteriecelle. De funktionelle implikationer overvejes derefter for hurtigt voksende celler, hvor effekten er ubetydelig, og for celler i stationær tilstand, hvor den kan forårsage en mærkbar lækage af ressourcer.
Vi overvejer f.eks. glycerol. Analysen vist i figur 2 giver et skøn over tidspunktet for dets lækage ud af cellen, hvis molekylet ikke fosforyleres eller på anden måde omdannes til en mere hydrofil form. Cellemembranens permeabilitet for glycerol er p≈10-100 nm/s (BNID 110824), som det kan aflæses af figur 1. Tidsskalaen for et glycerolmolekyl inde i cellen til at slippe tilbage til det omgivende medium, idet det antages, at der ikke er nogen returstrømning ind i cellen (cout=0), kan groft skønnes ved at bemærke, at udstrømningen fra cellen er p-A-cin, hvor A er celleoverfladearealet. Tidsskalaen findes ved at tage den samlede mængde i cellen, V-cin (hvor V er cellevolumen eller mere præcist cellens vandvolumen), og dividere med denne flux, hvilket for en bakteriecelle (r≈1 μm) resulterer i en tidsskala:
t =V-cin/p-A-cin =(4πr3/3)/(4πr2-3×10-6 cm/s) ≈ 10 s.
Dette er et groft skøn, fordi vi ikke har taget højde for den faldende koncentration af cin med tiden, som vil give en korrektionsfaktor på 1/ln(2), dvs. mindre end 2-fold stigning. Det, vi lærer af disse skøn, er, at hvis de glykolytiske mellemprodukter glyceraldehyd eller dihydroxyacetone, som minder meget om glycerol, ikke blev fosforyleret, hvilket resulterer i tilføjelse af en ladning, ville de gå tabt til mediet ved diffusion gennem cellemembranen. I laboratoriemedier, hvor en kulstofkilde tilføres i rigelige mængder, er dette ikke et stort problem, men i et naturligt miljø, hvor cellerne ofte venter i stationær fase på en heldig puls af næringsstoffer (E. coli menes at gennemgå måneder uden vækst efter udskillelse fra kroppen, før den finder en ny vært), kan cellen bremse sine tab ved at sørge for, at metaboliske mellemprodukter er mærket med en ladning, der forhindrer dem i at krydse den barriere, som lipiddobbeltlaget udgør.




