Byg højtydende tidsseriemodeller ved hjælp af Auto ARIMA i Python og R

Introduktion

Billede dig dette – Du har fået til opgave at forudsige prisen på den næste iPhone og har fået historiske data. Dette omfatter funktioner som kvartalsvise salg, udgifter fra måned til måned og en lang række ting, der følger med Apples balance. Hvilken type problem ville du som datalog klassificere dette som? Tidsseriemodellering, naturligvis.

Fra at forudsige salget af et produkt til at estimere husholdningernes elforbrug, er tidsserieprognoser en af de centrale færdigheder, som enhver datalog forventes at kende, hvis ikke beherske. Der findes et væld af forskellige teknikker derude, som du kan bruge, og vi vil i denne artikel dække en af de mest effektive, kaldet Auto ARIMA.

Vi vil først forstå begrebet ARIMA, som vil føre os til vores hovedemne – Auto ARIMA. For at størkne vores begreber vil vi tage et datasæt op og implementere det i både Python og R.

Indholdsfortegnelse

1. Hvad er en tidsserie?
2. Metoder til tidsserieprognoser
3. Indledning til ARIMA
4. Strin for ARIMA-implementering
5. Hvorfor har vi brug for AutoARIMA?
6. Auto ARIMA-implementering (på datasæt for flypassagerer)
7. Hvordan vælger auto ARIMA parametre?

Hvis du er fortrolig med tidsserier og deres teknikker (som glidende gennemsnit, eksponentiel udjævning og ARIMA), kan du springe direkte til afsnit 4. Nybegyndere kan starte med nedenstående afsnit, som er en kort introduktion til tidsserier og forskellige prognoseteknikker.

Hvad er en tidsserie?

Hvor vi lærer om teknikkerne til at arbejde med tidsseriedata, skal vi først forstå, hvad en tidsserie egentlig er, og hvordan den adskiller sig fra enhver anden form for data. Her er den formelle definition af tidsserier – Det er en serie af datapunkter målt med ensartede tidsintervaller. Det betyder ganske enkelt, at bestemte værdier registreres med et konstant interval, som kan være hver time, hver dag, hver uge, hver 10. dag osv. Det, der gør tidsserier anderledes, er, at hvert datapunkt i serien er afhængig af de foregående datapunkter. Lad os forstå forskellen tydeligere ved at tage et par eksempler.

Eksempel 1:

Sæt, at du har et datasæt af personer, der har taget et lån fra et bestemt firma (som vist i tabellen nedenfor). Tror du, at hver række vil være relateret til de foregående rækker? Bestemt ikke! Det lån, som en person tager, vil være baseret på hans økonomiske forhold og behov (der kan være andre faktorer som f.eks. familiestørrelse osv., men for enkelhedens skyld tager vi kun hensyn til indkomst og lånetype) . Desuden blev dataene ikke indsamlet i et bestemt tidsinterval. Det afhænger af, hvornår virksomheden modtog en anmodning om lånet.

Eksempel 2:

Lad os tage et andet eksempel. Lad os antage, at du har et datasæt, der indeholder niveauet af CO2 i luften pr. dag (skærmbillede nedenfor). Vil du være i stand til at forudsige den omtrentlige mængde CO2 for den næste dag ved at se på værdierne fra de sidste par dage? Ja, selvfølgelig. Hvis du observerer, er dataene blevet registreret på daglig basis, dvs. tidsintervallet er konstant (24 timer).

Du må have fået en fornemmelse af dette nu – det første tilfælde er et simpelt regressionsproblem og det andet et tidsserieproblem. Selv om tidsserie-puslespillet her også kan løses ved hjælp af lineær regression, men det er ikke rigtig den bedste fremgangsmåde, da den negligerer værdiernes relation til alle de relative tidligere værdier. Lad os nu se på nogle af de almindelige teknikker, der anvendes til løsning af tidsserieproblemer.

Metoder til tidsserieprognoser

Der findes en række metoder til tidsserieprognoser, og vi vil kort gennemgå dem i dette afsnit. Den detaljerede forklaring og python-koder for alle de nedenfor nævnte teknikker kan findes i denne artikel: 7 teknikker til tidsserieprognoser (med python-koder).

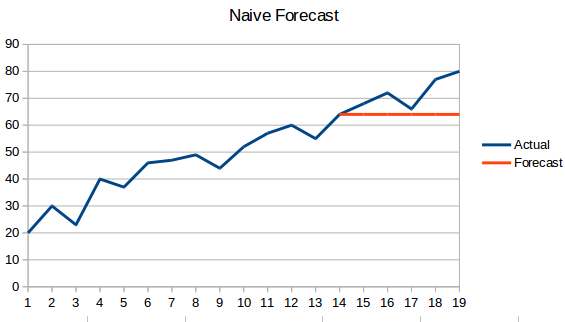
1. Naiv fremgangsmåde: I denne prognoseteknik forudsiges det, at værdien af det nye datapunkt er lig med det tidligere datapunkt. Resultatet vil være en flad linje, da alle nye værdier tager de tidligere værdier.
2. Simpelt gennemsnit: Den næste værdi tages som gennemsnittet af alle de tidligere værdier. Forudsigelserne her er bedre end “Naive Approach”, da det ikke resulterer i en flad linje, men her tages alle de tidligere værdier i betragtning, hvilket måske ikke altid er nyttigt. Når man f.eks. bliver bedt om at forudsige dagens temperatur, vil man tage hensyn til de sidste 7 dages temperatur i stedet for temperaturen for en måned siden.
3. Glidende gennemsnit : Dette er en forbedring i forhold til den foregående teknik. I stedet for at tage gennemsnittet af alle tidligere punkter tages gennemsnittet af ‘n’ tidligere punkter som den forudsagte værdi.
4. Vægtet glidende gennemsnit : Et vægtet glidende gennemsnit er et glidende gennemsnit, hvor de tidligere ‘n’ værdier tillægges forskellige vægte.
5. Simpel eksponentiel udjævning: I denne teknik tildeles større vægte til nyere observationer end til observationer fra en fjern fortid.
6. Holts lineære trendmodel: Denne metode tager hensyn til tendensen i datasættet. Med tendens menes seriens stigende eller faldende karakter. Hvis vi antager, at antallet af bookinger på et hotel stiger hvert år, kan vi sige, at antallet af bookinger viser en stigende tendens. Prognosefunktionen i denne metode er en funktion af niveau og tendens.
7. Holt Winters metode: Denne algoritme tager hensyn til både seriens tendens og sæsonudsving. For eksempel – antallet af bookinger på et hotel er højt i weekenden & lavt på hverdage og stiger hvert år; der eksisterer en ugentlig sæsonafhængighed og en stigende tendens.
8. ARIMA: ARIMA er en meget populær teknik til tidsseriemodellering. Den beskriver korrelationen mellem datapunkterne og tager hensyn til forskellen mellem værdierne. En forbedring i forhold til ARIMA er SARIMA (eller sæsonbestemt ARIMA). Vi vil se lidt mere detaljeret på ARIMA i det følgende afsnit.

Indledning til ARIMA

I dette afsnit vil vi lave en hurtig introduktion til ARIMA, som vil være nyttig for at forstå Auto Arima. En detaljeret forklaring af Arima, parametre (p,q,d), plots (ACF PACF) og implementering er inkluderet i denne artikel : Komplet tutorial til tidsserier.

ARIMA er en meget populær statistisk metode til tidsserieprognoser. ARIMA står for Auto-Regressive Integrated Moving Averages. ARIMA-modeller arbejder ud fra følgende antagelser –

• Dataserien er stationær, hvilket betyder, at middelværdien og variansen ikke må variere med tiden. En serie kan gøres stationær ved hjælp af logtransformation eller differentiering af serien.
• De data, der leveres som input, skal være en univariat serie, da arima bruger de tidligere værdier til at forudsige de fremtidige værdier.

ARIMA har tre komponenter – AR (autoregressiv term), I (differentieringsterm) og MA (glidende gennemsnitsterm). Lad os forstå hver af disse komponenter –

• AR-terminen henviser til de tidligere værdier, der anvendes til at forudsige den næste værdi. AR-terminen er defineret af parameteren “p” i arima. Værdien af ‘p’ bestemmes ved hjælp af PACF-plottet.
• MA-terminen anvendes til at definere antallet af tidligere prognosefejl, der anvendes til at forudsige de fremtidige værdier. Parameteren “q” i arima repræsenterer MA-terminen. ACF-plotet bruges til at identificere den korrekte ‘q’-værdi.
• Differentieringsrækkefølge angiver antallet af gange, differentieringsoperationen udføres på serien for at gøre den stationær. Test som ADF og KPSS kan bruges til at bestemme, om serien er stationær, og hjælper med at identificere d-værdien.

Strin til ARIMA-implementering

De generelle trin til implementering af en ARIMA-model er –

1. Indlæs dataene: Det første skridt til modelopbygning er naturligvis at indlæse datasættet
2. Forbehandling: Afhængigt af datasættet vil trinene i forbehandlingen blive defineret. Dette vil omfatte oprettelse af tidsstempler, konvertering af dtype af dato/tidskolonne, gøre serierne univariate osv.
3. Gør serierne stationære: For at opfylde antagelsen er det nødvendigt at gøre serien stationær. Dette vil omfatte kontrol af seriens stationæritet og udførelse af de nødvendige transformationer
4. Bestem d-værdien: For at gøre serien stationær vil antallet af gange, hvor forskelsoperationen blev udført, blive taget som d-værdi
5. Opret ACF- og PACF-plots: Dette er det vigtigste trin i ARIMA-implementeringen. ACF PACF-plots bruges til at bestemme inputparametrene for vores ARIMA-model
6. Bestem p- og q-værdierne: Læs værdierne for p og q fra plottet i det foregående trin
7. Tilpas ARIMA-modellen: Ved hjælp af de behandlede data og de parameterværdier, vi har beregnet fra de foregående trin, tilpasses ARIMA-modellen
8. Forudsig værdier på valideringssættet: Forudsig de fremtidige værdier
9. Beregn RMSE: For at kontrollere modellens ydeevne kontrolleres RMSE-værdien ved hjælp af forudsigelserne og de faktiske værdier på valideringssættet

Hvorfor har vi brug for Auto ARIMA?

Og selv om ARIMA er en meget kraftfuld model til at forudsige tidsseriedata, ender dataforberedelses- og parameterindstillingsprocesserne med at være meget tidskrævende. Før du implementerer ARIMA, skal du gøre serien stationær og bestemme værdierne for p og q ved hjælp af de plot, vi har diskuteret ovenfor. Auto ARIMA gør denne opgave virkelig enkel for os, da den eliminerer trin 3 til 6, som vi så i det foregående afsnit. Nedenfor er de trin, du skal følge for at implementere auto ARIMA:

1. Lad dataene ind: Dette trin vil være det samme. Indlæs dataene i din notesbog
2. Forbehandling af data: Input skal være univariate, drop derfor de andre kolonner
3. Fit Auto ARIMA: Fit modellen på de univariate serier
4. Predict values on validation set: Gør forudsigelser på valideringssættet
5. Beregn RMSE: Kontroller modellens ydeevne ved hjælp af de forudsagte værdier i forhold til de faktiske værdier

Vi gik helt uden om valget af p- og q-funktionen, som du kan se. Sikke en lettelse! I næste afsnit vil vi implementere auto ARIMA ved hjælp af et legetøjsdatasæt.

Implementering i Python og R

Vi vil bruge datasættet International-Air-Passenger. Dette datasæt indeholder månedlige totaler af antallet af passagerer (i tusinder). Det har to kolonner – måned og antal passagerer. Du kan downloade datasættet fra dette link.

#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)

output -76.51355764316357

Nedenfor er R-koden til samme problem:

# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)

Hvordan vælger Auto Arima de bedste parametre

I ovenstående kode har vi blot brugt .fit() kommandoen til at tilpasse modellen uden at skulle vælge kombinationen af p, q, d. Men hvordan fandt modellen ud af den bedste kombination af disse parametre? Auto ARIMA tager hensyn til de genererede AIC- og BIC-værdier (som du kan se i koden) for at bestemme den bedste kombination af parametre. AIC-værdierne (Akaike Information Criterion) og BIC-værdierne (Bayesian Information Criterion) er estimatorer til at sammenligne modeller. Jo lavere disse værdier er, jo bedre er modellen.

Kig på disse links, hvis du er interesseret i matematikken bag AIC og BIC.

Slutnoter og yderligere læsning

Jeg har fundet auto ARIMA som den enkleste teknik til at udføre tidsserieprognoser. Det er godt at kende en genvej, men det er også vigtigt at være bekendt med matematikken bag den. I denne artikel har jeg skimmet gennem detaljerne i, hvordan ARIMA fungerer, men sørg for at gennemgå de links, der er angivet i artiklen. For din nemme reference er her linksene igen:

• En omfattende vejledning for begyndere til tidsserieprognoser i Python
• Komplet vejledning til tidsserier i R
• 7 teknikker til tidsserieprognoser (med python-koder)

Jeg vil foreslå at praktisere det, vi har lært her, på dette praksisproblem: Time Series Practice Problem. Du kan også tage vores kursus, der er oprettet på det samme praksisproblem: Time series forecasting, for at give dig et forspring.