K získání teplotní závislosti \(K\)
\}{∂T} můžeme použít Gibbsovu-Helmholtzovu rovnici. \right)_P = \dfrac{-Δ_rH^o}{T^2}\]
Při rovnováze můžeme \(Δ_rG^o\) přirovnat k \(-RT\ln K\), takže dostaneme:
\}{∂T} \right)_P = \dfrac{Δ_rH^o}{RT^2} \]
Vidíme, že to, zda \(K\) s teplotou roste nebo klesá, souvisí s tím, zda je entalpie reakce kladná nebo záporná. Pokud se teplota mění dostatečně málo, aby bylo možné považovat \(Δ_rH^o\) za konstantní, můžeme hodnotu \(K\) při jedné teplotě převést na jinou integrací výše uvedeného výrazu, dostaneme podobné odvození jako u deprese bodu tání:
\
Pokud je požadována větší přesnost, mohli bychom korigovat teplotní změny ΔrHo pomocí údajů o tepelné kapacitě.
Jak se \(K\) zvyšuje nebo snižuje s teplotou, souvisí s tím, zda je reakční entalpie kladná nebo záporná.
Výraz pro \(K\) je poměrně citlivou funkcí teploty vzhledem k jeho exponenciální závislosti na rozdílu stechiometrických koeficientů Jedním ze způsobů, jak si uvědomit citlivou závislost rovnovážných konstant na teplotě, je připomenout, že
\
Však, protože za konstantního tlaku a teploty
\
Rovnice \(\ref{18}\) se stává
\
Přirozeným logaritmováním obou stran získáme lineární vztah mezi \(\ln K \)a standardními entalpiemi a entropiemi:
\
který je známý jako van’t Hoffova rovnice. Z ní vyplývá, že graf závislosti \(\ln K\) na \(1/T\) by měl být přímkou se sklonem \(-\Delta_r{H^o}/R\) a průsečíkem \(\Delta_r{S^o}/R\).
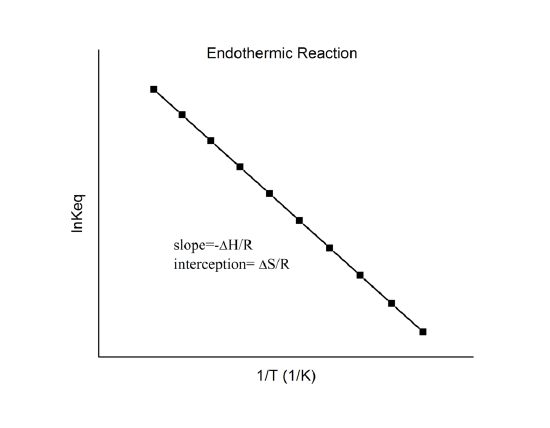
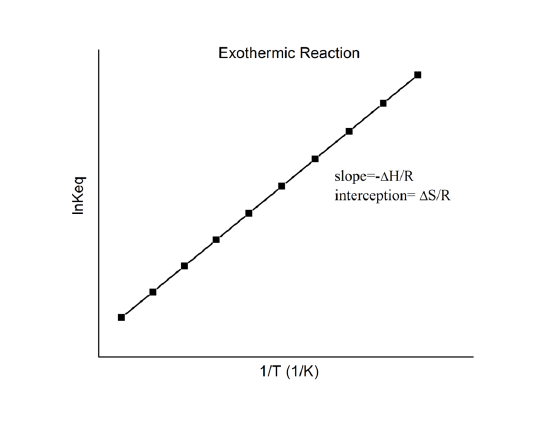
Tyto veličiny lze tedy určit z údajů \(\ln K\) vs. \(1/T\) bez provedení kalorimetrie. Hlavním předpokladem zde samozřejmě je, že \(\Delta_r{H^o}\) a \(\Delta_r{S^o}\) jsou jen velmi slabě závislé na \(T\), což obvykle platí.
Přispěvatelé a atributy
.