Simetria punctiformă există atunci când figura este desenată în jurul unui singur punct.

Acest punct se numește centrul figurii sau centrul de simetrie. În figura alăturată, observăm că, corespunzător punctului X de pe figură, există un punct X’ de cealaltă parte a centrului care este direct opus lui X și se află pe figură. Spunem că figura este simetrică în raport cu centrul.
Nota:
Când rotim o figură cu 180° și aceasta își recapătă forma inițială, atunci spunem că există simetrie punctiformă în figură.
Exemple de figuri care prezintă simetrie punctiformă:
● Toate literele alfabetului englezesc.
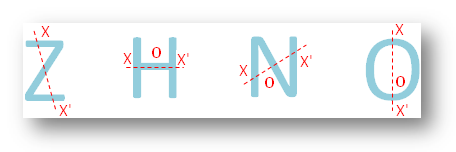
● Diferite figuri geometrice.
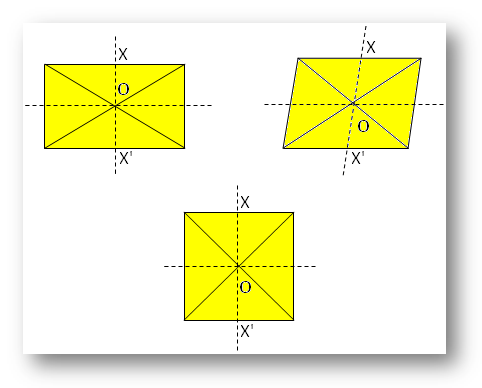
Nota:
Aici, O estecentrul de simetrie.
Cu privire la X există X’, astfel încât X’ să fie direct opus lui X pe partea cealaltă a lui O.
Care sunt condițiile pe care le îndeplinește o formă sau o figură pentru simetria punctiformă?
Condițiile pe care le îndeplinește o formă sau o figură pentru simetria punctiformă și anume: fiecare parte trebuie să aibă o parte corespunzătoare
– distanța trebuie să fie egală față de punctul central
– dar trebuie să fie în sens opus.
● Concepte înrudite
● Simetrie liniară
● Linii de simetrie
● Simetrie de rotație
● Ordinea simetriei de rotație
● Tipuri de simetrie
● Reflexie
● Reflexia unui punct în x-axis
● Reflecția unui punct în axa y-axis
● Reflexia unui punct în origine
● Rotație
● Rotație de 90 de grade în sensul acelor de ceasornic
● Rotație de 90 de grade în sens invers acelor de ceasornic
● Rotație de 180 de grade
.
Probleme de matematică de clasa a VII-a
Practică de matematică de clasa a VIII-a
De la simetria punctiformă la PAGINA DE ACASĂ
.