Introducerea sticlei Klein

Dacă vă place să beți, atunci o sticlă Klein nu este un recipient recomandat. Poate că seamănă vag cu o sticlă, dar nu înconjoară niciun volum, ceea ce înseamnă că nu poate conține efectiv niciun lichid. Tot ceea ce turnați „înăuntru” va ieși din nou.

Cum se construiește un lucru atât de ciudat și de ce ați vrea să-l construiți? Matematicianul Felix Klein, care a descoperit sticla în 1882, a descris-o ca pe o suprafață care „poate fi vizualizată prin răsturnarea unei bucăți de tub de cauciuc și lăsând-o să treacă prin ea însăși, astfel încât exteriorul și interiorul să se întâlnească”.

Your browser does not support the video tag.Direct link

Este evident că sticla Klein, la fel ca și mai cunoscuta sferă, este o suprafață închisă: este finită în sensul că o poți încadra într-o regiune finită a spațiului, dar o furnică s-ar putea plimba pe ea la nesfârșit fără să întâlnească vreodată o limită sau să cadă peste o margine. Spre deosebire de sferă, care are un interior și un exterior, sticla Klein este unilaterală: plimbându-se, furnica noastră ar putea ajunge la ambele părți ale fiecărui punct al suprafeței. Acesta este motivul pentru care sticla nu închide niciun volum și răspunde, de asemenea, la întrebarea „de ce”: sticla Klein este interesantă pentru că nu întâlnim multe forme unilaterale în natură. (Vedeți aici o altă imagine foarte frumoasă a unei sticle Klein.)

Fâșia lui Möbius este unilaterală – vedeți versiunea animată. (Imagine și animație de Konrad Polthier.)

Dacă acest lucru este puțin confuz, gândiți-vă la un exemplu mai simplu de suprafață unilaterală: faimoasa bandă Möbius. Puteți realiza una luând două capete ale unei benzi de hârtie, dându-i o răsucire și apoi lipind capetele împreună. Dacă folosiți o bandă de hârtie ale cărei două fețe au culori diferite, de exemplu verde și portocaliu, este ușor să vă convingeți că banda Möbius rezultată este unilaterală. După ce ați răsucit și lipit, veți descoperi că puteți ajunge la fiecare punct portocaliu din fiecare punct verde fără a fi nevoie să străpungeți hârtia sau să vă cățărați pe marginea ei.

În ciuda sticlei Klein, banda Möbius are o limită – aceasta este formată din cele două margini nelipite ale benzii originale. Dar există o legătură între cele două. Dacă luați două benzi Möbius și creați o formă închisă prin unirea limitelor lor folosind o bandă obișnuită cu două fețe, așa cum se arată mai jos, ceea ce obțineți este exact sticla Klein.

Your browser does not support the video tag.Legătură directă

Acest fapt l-a inspirat pe matematicianul Leo Moser să compună un limerick:

Un matematician pe nume KleinCredea că banda lui Möbius este divină.Spunea el: „Dacă lipești marginile a două,Vei obține o sticlă ciudată ca a mea.”

Câțiva matematicieni chiar au multiple talente!

O altă trăsătură curioasă a sticlei lui Klein este că se intersectează pe ea însăși, ceea ce înseamnă că este greu să o faci dintr-un singur tub de cauciuc, așa cum a sugerat Klein. Strict vorbind, obiectul care se auto-intersectează descris mai sus nu este o sticlă Klein, ci (așa cum a indicat Klein) doar o vizualizare a uneia. Pentru a înțelege de ce, gândiți-vă mai întâi la mai cunoscuta gogoașă (cunoscută matematic sub numele de torus). Puteți realiza un torus dintr-o foaie pătrată de cauciuc lipind mai întâi două laturi opuse pentru a forma un cilindru, iar apoi lipind cele două componente limită ale acelui cilindru pentru a obține torusul.

Facerea unui torus: Mai întâi lipiți puncte opuse pe două laturi opuse ale pătratului pentru a obține un cilindru și apoi lipiți cele două cercuri de frontieră ale acelui cilindru (care corespund lipirii punctelor opuse de pe celelalte două laturi ale pătratului) pentru a forma un torus.

Dacă nu doriți să vă deranjați cu lipirea, vă puteți gândi pur și simplu la torus ca la un pătrat, ținând cont de faptul că punctele opuse de pe laturile opuse sunt considerate la fel. Astfel, atunci când glisați o formă desenată pe „pătrat” peste marginea de sus, aceasta va reapărea la marginea de jos, iar când o glisați peste marginea din dreapta va reapărea la marginea din stânga (și invers).

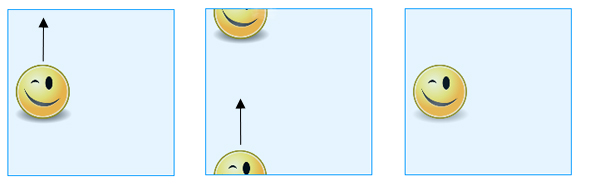Când glisați o formă desenată pe „pătrat” peste marginea de sus, aceasta va reapărea la marginea de jos.

Pentru a obține o adevărată sticlă Klein, începeți în același mod, identificând puncte opuse pe o pereche de laturi opuse ale unui pătrat. Pentru cealaltă pereche de laturi, însă, nu identificați puncte care sunt direct opuse, ci puncte care sunt opuse pe diagonală, așa cum se arată în imagine.

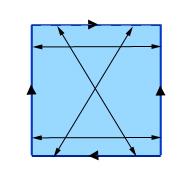
Facerea unei sticle Klein: identificați punctele opuse a două laturi opuse (cele verticale din această imagine) și apoi identificați punctele opuse în diagonală pe cele două laturi rămase. (Dacă etichetați punctele de pe laturile de sus și de jos, de la stânga la dreapta, cu numerele de la 0 la 1, atunci un punct cu eticheta x de pe latura de sus se identifică cu punctul cu eticheta 1-x de pe latura de jos.)

Obiectul rezultat este sticla Klein. Din nou, vă puteți gândi la ea ca la un pătrat, ținând cont de punctele de frontieră care sunt considerate identice. Dacă glisați o formă peste una dintre marginile pe care au fost identificate puncte opuse (verticală în imaginea noastră), aceasta reapare reapare pe partea opusă, ca mai înainte. Dacă, însă, o glisați peste una dintre marginile ale căror puncte au fost identificate pe diagonală (orizontală în imaginea noastră), ea apare pe partea opusă, dar deplasată și ca o imagine în oglindă a ei inițială.

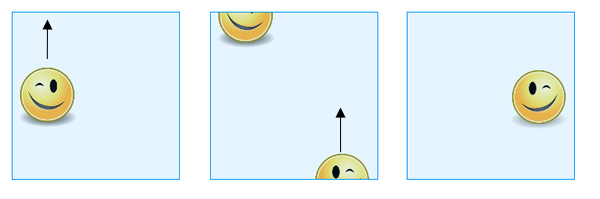
Dacă glisați o formă peste muchia de sus, ea apare peste muchia de jos, dar deplasată pe partea cealaltă și ca o imagine în oglindă a sinelui său original.

Singura modalitate de a construi această formă în spațiul tridimensional prin lipirea efectivă a punctelor este de a-i permite să se intersecteze pe sine. Acest lucru echivalează cu identificarea unor perechi de puncte în interiorul pătratului original, astfel încât, strict vorbind, forma rezultată nu este exact aceeași cu sticla Klein, care are doar punctele de frontieră identificate. Este doar o modalitate de reprezentare a sticlei în spațiul tridimensional (mai există și altele).

În mod curios, conceptele de „interior”, „exterior” și „unilateralitate” depind de spațiul ambiant în care se află un obiect. De exemplu, o buclă desenată pe o bucată de hârtie (în spațiul bidimensional) are un interior și un exterior bine definite, dar o buclă desenată în spațiul tridimensional nu are. Acesta este motivul pentru care nu putem vorbi despre unilateralitate decât dacă decidem mai întâi cum să încorporăm o suprafață în spațiul tridimensional. Cu toate acestea, există o proprietate strâns legată de aceasta, care este intrinsecă unei forme și nu depinde de spațiul înconjurător. O suprafață se numește orientabilă dacă nu se poate glisa o formă desenată pe ea în jurul și înapoi la locul de unde a pornit, astfel încât să arate ca propria imagine în oglindă. După cum puteți vedea în animația care însoțește imaginea din dreapta, banda lui Möbius nu este orientabilă. Și, după cum puteți vedea în imaginea cu fața zâmbitoare de mai sus, nici sticla Klein nu este. pentru a-i da o descriere matematică completă, sticla Klein este o suprafață închisă, neorientabilă. Pentru a afla mai multe despre ea, consultați articolul Inside the Klein bottle.

Despre autor

Marianne Freiberger este redactor al revistei Plus.

.