Înainte de a începe, trebuie să facem câteva presupuneri.
În primul rând, lucrăm cu fluide newtoniene. Acesta este cel mai simplu mod matematic de a lua în considerare vâscozitatea într-un fluid. Nu există fluide reale care să se încadreze perfect în această categorie, dar, în majoritatea cazurilor, aerul și apa pot fi tratate ca un fluid newtonian. Cealaltă ipoteză foarte importantă pe care o facem este că fluidul este incompresibil. Aceasta înseamnă că densitatea sa, rho, este o constantă.
Conservarea masei

Prima ecuație ne spune că masa fluidului pe care lucrăm se conservă. Fluidul își poate schimba forma, dar această ecuație ne spune că masa este aceeași de la început până la sfârșit.
Acum să vorbim despre matematică. Litera u reprezintă viteza fluidului și este un vector. Are trei componente, le putem numi u, v, w și ele reprezintă viteza fluidului în direcțiile x, y și z. Litera greacă nabla ∇ urmată de un punct reprezintă operatorul de divergență. Aceasta înseamnă că trebuie să diferențiem componentele sale în fiecare direcție (în acest caz x, y, z).

Prima derivată ne spune cum se modifică componenta x a vitezei pe măsură ce ne deplasăm pe direcția x. Același lucru este valabil și pentru celelalte două derivate. Deoarece această ecuație este egală cu zero, ea ne arată că masa este conservată.
Conservarea impulsului

Cea de-a doua ecuație este de fapt un set de trei ecuații diferențiale. Aceasta este cea care poate fi descrisă ca a doua lege a lui Newton pentru fluide. Dacă extindem expresia obținem un sistem complex.
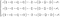
Din moment ce este mult mai simplu de înțeles, ne vom concentra pe conservarea impulsului neexpansat.
Când lucrăm cu fluide putem spune că masa și densitatea sunt aceleași lucruri (atâta timp cât volumul lor este același). Dacă avem în vedere două fluide, putem spune că cel mai dens este cel mai „greu” (de exemplu, mercurul și apa). În acest caz, litera greacă ρ (rho) reprezintă densitatea fluidului.
Avem masa, acum, pentru a ne întoarce la a doua lege a lui Newton, avem nevoie de accelerație. Aceasta este exact rezultatul derivatei în timp a vectorului viteză.

Acum, tot ce ne-a mai rămas sunt termenii din partea dreaptă a semnului egal, iar aceștia reprezintă toate forțele care sunt aplicate fluidului.
Primul termen ∇p este gradientul presiunii. Acesta reprezintă diferența de presiune în spațiul în care este conținut fluidul. De exemplu, dacă există o zonă cu presiune scăzută și o alta cu o presiune mai mare, fluidul se va deplasa din secțiunea cu presiune ridicată în cea cu presiune mai scăzută. Gradientul lui p spune toate acestea.
Cel de-al doilea termen descrie vâscozitatea fluidului. Gândiți-vă la două lichide diferite, cum ar fi apa și mierea. Când turnați un pahar cu apă, aceasta cade rapid și ușor. Când faceți același lucru cu mierea, aceasta este lipicioasă și se toarnă foarte încet. Aceasta este ceea ce spune această expresie.
Ultimul termen, F, este cel mai ușor, deoarece reprezintă toate forțele externe care pot fi aplicate acelui fluid. De obicei, forța pe care o luăm în considerare aici este gravitația.
Aceasta este, toate acele simboluri și litere fanteziste înseamnă doar forță = masă x accelerație.
Utilizarea ecuațiilor Navier-Stokes
Din moment ce rezolvarea acestor ecuații este atât de complicată, pentru a le folosi trebuie să facem o mulțime de aproximări. Câteva exemple sunt curgerea Poiseuille și Couette. Cu o mulțime de ipoteze, acești doi oameni de știință au reușit să găsească o soluție la ecuațiile Navier-Stokes pentru o aplicație foarte specifică. Cu toate acestea, dacă vrem să le folosim pentru o sarcină mai complicată, cum ar fi previziunile meteo, trebuie să facem altceva.
Cel mai comun mod de a folosi aceste ecuații este prin transformarea lor, cu media Reynolds. Acesta este un proces matematic avansat, iar rezultatele sunt ecuațiile Reynolds. Acestea se numesc de obicei ecuații RANS (care înseamnă ecuații Navier-Stokes cu media Reynolds).
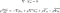
Aceste ecuații sunt utilizate atunci când fluidul se află într-un flux turbulent. Ele arată aproape exact ca ecuațiile Navier-Stokes, cu excepția ultimului termen. Acesta se numește tensorul de tensiune Reynolds. Este cantitatea care ne permite să ținem cont de turbulența din fluid.
În ecuațiile RANS, cantitățile pe care le folosim sunt mediate pe un interval de timp. Acest interval trebuie să fie suficient de mic pentru a permite observarea fenomenului pe care îl studiem. În același timp, trebuie să fie suficient de mare pentru a face ca efectul turbulenței să-și piardă din importanță.
Cu ipotezele corecte, aceste ecuații funcționează. Știm cum să le folosim pentru a face mașinile de Formula 1 mai rapide, pentru a face o navă spațială să ajungă la ISS și pentru a face prognoza meteo. Așa că poate vă întrebați de ce dovada acestor ecuații valorează un milion de dolari?
Un premiu de un milion de dolari
Din punct de vedere al fizicii, aceste ecuații sunt doar a doua lege a lui Newton care funcționează cu fluide. Atunci când facem unele presupuneri și unele simplificări, putem face lucruri uimitoare cu ele.
Reala problemă este aceasta. Rezolvarea acestor ecuații fără aproximări este pur și simplu îngrozitor de complicată. Este atât de dificil încât nu s-a dovedit că soluțiile există cu adevărat. Și aici intervine Premiul Mileniului.
Declarația oficială a problemei (o găsiți aici) este:
Probați sau dați un contra-exemplu al următoarei afirmații: în trei dimensiuni spațiale și în timp, dat fiind un câmp de viteză inițial, există un câmp vectorial de viteză și un câmp scalar de presiune, care sunt ambele netede și definite global, care rezolvă ecuațiile Navier-Stokes.
Ce înseamnă că pentru a câștiga premiul trebuie să faceți trei lucruri:
- Demonstrați că există o soluție
- Soluția trebuie să existe în fiecare punct din spațiu
- Soluția trebuie să fie netedă. Aceasta înseamnă că o mică schimbare a condițiilor inițiale produce doar o mică variație a rezultatului.
Pentru un inginer este de obicei suficient să știe că aceste ecuații funcționează, chiar dacă doar la un anumit nivel de aproximare. Cu toate acestea, pentru un matematician este foarte important să știe dacă soluțiile există și cum se comportă.
Poate că acum vă gândiți că, dacă ele funcționează așa cum sunt, cheltuirea de timp și energie în căutarea unei demonstrații este o pierdere totală de timp. Ei bine, la fel ca multe progrese tehnologice din istoria omenirii, rezultatul poate să nu pară foarte important. Ceea ce este important este calea pentru a ajunge acolo, care poate aduce noi cunoștințe și îmbunătățiri în viața noastră.
Gândiți-vă la misiunile spațiale. Dacă oamenii nu ar fi decis niciodată să meargă și să pășească pe Lună, nu am fi avut multe obiecte care sunt folosite pentru a ne îmbunătăți viața. Aparatele RMN și stimulatoarele cardiace provin din tehnologii dezvoltate pentru explorarea spațială. Astăzi, medicii din întreaga lume le folosesc în fiecare zi pentru a salva vieți. Același lucru se aplică și aici. Calea spre descoperirea soluției ecuațiilor Navier-Stokes ne va ajuta să ne îmbunătățim înțelegerea fluidelor și nu numai. Ne poate conduce la noi descoperiri și va necesita, probabil, inventarea de noi calcule matematice. Aceasta poate fi apoi folosită pentru a răspunde la multe alte probleme, pentru a inventa noi tehnologii care să ne îmbunătățească viața și să ne facă mai buni.
.