Construirea triunghiului echilateral – MathBitsNotebook (Geo

Triunghiul echilateral MathBitsNotebook.com Schemă tematică | Schemă de geometrie | Resurse pentru profesori MathBits’ Teacher Resources Condiții de utilizare Persoană de contact: Donna Roberts

Utilizați doar compasul și muchia dreaptă atunci când desenați o construcție. Nu desenați cu mâna liberă!

Vom face TREI construcții ale unui triunghi echilateral. Prima va consta în construirea unui triunghi echilateral dată fiind lungimea unei laturi, iar celelalte două vor consta în construirea unui triunghi echilateral înscris într-un cerc.

Dată: lungimea unei laturi a triunghiului Constituie: un triunghi echilateral

ETAPE:
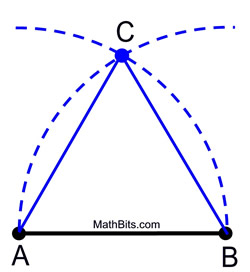
1. Așezați punctul de compas pe A și măsurați distanța până la punctul B. Învârtiți un arc de această mărime deasupra (sau sub) segmentului.
2. Fără a schimba intervalul pe compas, așezați punctul de compas pe B și învârtiți același arc, care se intersectează cu primul arc.
3. Etichetați punctul de intersecție ca fiind al treilea vârf al triunghiului echilateral.

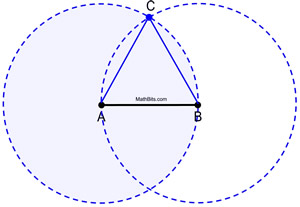
Vedeți cercurile pline la lucru.

Demonstrație de construcție: Cercul A este congruent cu cercul B, deoarece fiecare dintre ele a fost format folosind aceeași lungime a razei, AB. Deoarece AB și AC sunt lungimi ale razelor cercului A, ele sunt egale între ele. În mod similar, AB și BC sunt raze ale cercului B și sunt egale între ele. Prin urmare, AB = AC = BC prin substituție (sau proprietate tranzitivă). Deoarece segmentele congruente au lungimi egale, și ΔABC este echilateral (având trei laturi congruente).

ETAPE:
1. Așezați punctul de compas pe hârtie și desenați un cerc. (Păstrați această întindere a compasului!)
2. Așezați un punct, etichetat A, oriunde pe circumferința cercului pentru a acționa ca punct de plecare.
3. Fără a schimba întinderea pe compas, plasați punctul de compas pe A și învârtiți un arc mic care traversează circumferința cercului.
4. Fără a schimba întinderea pe compas, mutați punctul de compas la intersecția arcului anterior cu circumferința și faceți un alt arc mic pe circumferința cercului.
5. Continuați să repetați acest proces de „pășire” în jurul cercului până când vă întoarceți la punctul A.
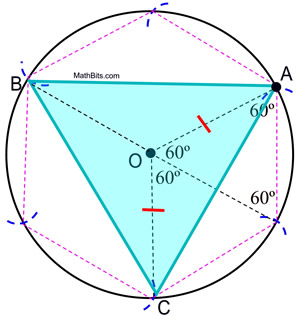
6. Pornind de la A, conectați fiecare alt arc de cerc pentru a forma triunghiul echilateral.

Referiți-vă la demonstrația unui hexagon regulat înscris pentru mai multe informații referitoare la demonstrația acestei construcții.

Demonstrația construcției: Demonstrația hexagonului regulat înscris arată că unghiurile centrale ale unui hexagon regulat conțin 60º. Unghiurile centrale ale triunghiului înscris în acest cerc conțin 120º. Deoarece ΔAOC este isoscel (OA și OC sunt lungimile razelor), m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC ΔCOB ΔBOA prin SAS. Prin CPCTC, ∠OCB ∠OCA și m∠OCB = 30º prin substituție și m∠BCA = 60º. În mod similar, avem m∠ACB = m∠CBA = m∠CBA = m∠BAC = 60º și echilateral ΔABC.

ETAPE:
1. Așezați vârful compasului pe hârtie și desenați un cerc, O. (Păstrați această întindere a compasului!)
2. Folosind o rigla, desenați un diametru al cercului, etichetând punctele de capăt P și B.
3. Fără a schimba întinderea compasului, așezați vârful compasului pe P și desenați un cerc întreg.
4. Etichetați punctele de intersecție ale celor două circumferințe ale cercului cu A și C.
5. Desenați segmente de la A la B, B la C și C la A, pentru a forma triunghiul echilateral.

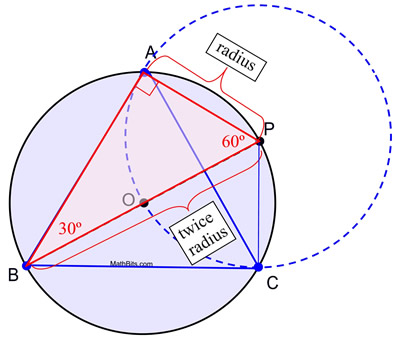
Dovada construcției: Această construcție se folosește de faptul că un unghi înscris într-un semicerc este un unghi drept și că într-un triunghi de 30º-60º-90º, lungimea piciorului scurt este jumătate din lungimea ipotenuzei. În această construcție, cercul O și cercul P sunt congruente, deoarece au aceeași lungime a razei. AP este o lungime de rază a cercului P, iar razele AP = OP. OP este, de asemenea, o lungime de rază a cercului O (împreună cu OB) și diametrul BP = BO + OP = 2 OP. Prin substituție, BP = 2 AP, creând condițiile necesare pentru m∠ABP = 30º. În consecință, m∠APB = 60º. Un argument similar poate fi folosit pentru a stabili că pentru ΔPBC, m∠PBC = 30º și m∠BPC = 60º, ceea ce face ca ΔPBC să fie ΔPBA prin ASA (cu latura comună de la B la P).
Acum, deoarece acestea sunt laturile corespunzătoare ale celor două triunghiuri congruente, ceea ce face ca ΔABC să fie isoscel. ∠BAC ∠BCA, deoarece unghiurile de bază ale unui triunghi isoscel sunt congruente.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º prin postulatul adunării unghiurilor și prin substituție. m∠BAC + m∠BCA + m∠ABC + m∠ABC = 180º deoarece suma măsurilor unghiurilor dintr-un triunghi este 180º. Deoarece m∠BAC + m∠BAC + 60º = 180º prin substituție, știm că 2m∠BAC = 120º și m∠BAC = 60º. În consecință, m∠BCA este de asemenea egal cu 60º prin substituție, ceea ce face ca ΔABC să fie echilateral.