Introducere
Imaginați-vă acest lucru – Vi s-a încredințat sarcina de a prognoza prețul următorului iPhone și ați primit date istorice. Acestea includ caracteristici precum vânzările trimestriale, cheltuielile de la o lună la alta și o serie întreagă de lucruri care vin cu bilanțul Apple. În calitate de cercetător de date, la ce tip de problemă ați clasifica acest lucru? Modelarea seriilor temporale, bineînțeles.
De la prezicerea vânzărilor unui produs până la estimarea consumului de energie electrică al gospodăriilor, prognoza seriilor temporale este una dintre competențele de bază pe care orice om de știință de date trebuie să le cunoască, dacă nu chiar să le stăpânească. Există o multitudine de tehnici diferite pe care le puteți utiliza, iar în acest articol vom aborda una dintre cele mai eficiente, numită Auto ARIMA.

Primul lucru pe care îl vom înțelege este conceptul de ARIMA, care ne va conduce la subiectul nostru principal – Auto ARIMA. Pentru a ne consolida conceptele, vom prelua un set de date și îl vom implementa atât în Python, cât și în R.
Tabel de conținut
- Ce este o serie de timp?
- Metode de prognoză a seriilor de timp
- Introducere la ARIMA
- Pași pentru implementarea ARIMA
- De ce avem nevoie de AutoARIMA?
- Implementarea Auto ARIMA (pe setul de date privind pasagerii aerieni)
- Cum selectează parametrii Auto ARIMA?
Dacă sunteți familiarizați cu seriile de timp și cu tehnicile sale (cum ar fi media mobilă, netezirea exponențială și ARIMA), puteți sări direct la secțiunea 4. Pentru începători, începeți de la secțiunea de mai jos, care este o scurtă introducere în seriile de timp și în diverse tehnici de prognoză.
Ce este o serie de timp?
Înainte de a învăța despre tehnicile de lucru cu date din serii de timp, trebuie să înțelegem mai întâi ce este de fapt o serie de timp și cum se deosebește aceasta de orice alt tip de date. Iată definiția formală a seriilor de timp – Este o serie de puncte de date măsurate la intervale de timp consistente. Acest lucru înseamnă pur și simplu că anumite valori sunt înregistrate la un interval constant care poate fi orar, zilnic, săptămânal, la fiecare 10 zile și așa mai departe. Ceea ce face ca seriile de timp să fie diferite este faptul că fiecare punct de date din serie este dependent de punctele de date anterioare. Să înțelegem mai bine diferența prin câteva exemple.
Exemplul 1:
Să presupunem că aveți un set de date de persoane care au luat un împrumut de la o anumită companie (așa cum se arată în tabelul de mai jos). Credeți că fiecare rând va fi legat de rândurile anterioare? Cu siguranță că nu! Împrumutul luat de o persoană se va baza pe condițiile și nevoile sale financiare (ar putea exista și alți factori, cum ar fi mărimea familiei etc., dar pentru simplificare luăm în considerare doar venitul și tipul de împrumut) . De asemenea, datele nu au fost colectate la un anumit interval de timp. Depinde de momentul în care compania a primit o cerere de împrumut.

Exemplu 2:
Să luăm un alt exemplu. Să presupunem că aveți un set de date care conține nivelul de CO2 din aer pe zi (captura de ecran de mai jos). Veți putea să preziceți cantitatea aproximativă de CO2 pentru ziua următoare uitându-vă la valorile din ultimele câteva zile? Bineînțeles că da. Dacă observați, datele au fost înregistrate zilnic, adică intervalul de timp este constant (24 de ore).

În acest moment trebuie să fi intuit acest lucru – primul caz este o problemă de regresie simplă, iar cel de-al doilea este o problemă de serie temporală. Deși puzzle-ul seriei temporale de aici poate fi rezolvat și cu ajutorul regresiei liniare, dar aceasta nu este chiar cea mai bună abordare, deoarece neglijează relația valorilor cu toate valorile relative din trecut. Să analizăm acum câteva dintre tehnicile comune utilizate pentru rezolvarea problemelor de serii de timp.
Metode de prognoză a seriilor de timp
Există o serie de metode de prognoză a seriilor de timp și le vom aborda pe scurt în această secțiune. Explicația detaliată și codurile python pentru toate tehnicile menționate mai jos pot fi găsite în acest articol: 7 tehnici de prognoză a seriilor de timp (cu coduri python).
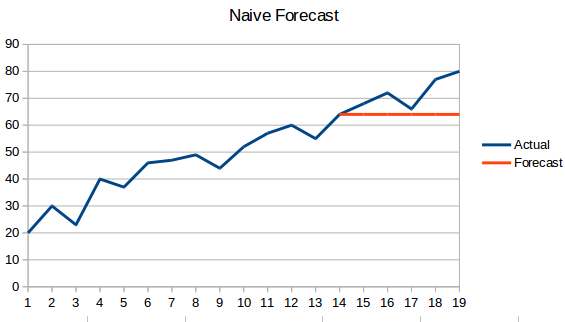
- Naive Approach: În această tehnică de prognoză, se prezice că valoarea noului punct de date este egală cu cea a punctului de date anterior. Rezultatul ar fi o linie plată, deoarece toate valorile noi preiau valorile anterioare.
- Media simplă: Următoarea valoare este luată ca medie a tuturor valorilor anterioare. Predicțiile de aici sunt mai bune decât „Abordarea naivă”, deoarece nu rezultă o linie plată, dar aici sunt luate în considerare toate valorile anterioare, ceea ce ar putea să nu fie întotdeauna util. De exemplu, atunci când vi se cere să preziceți temperatura de astăzi, veți lua în considerare temperatura din ultimele 7 zile, mai degrabă decât temperatura de acum o lună.

- Media mobilă : Aceasta este o îmbunătățire față de tehnica anterioară. În loc să se ia media tuturor punctelor anterioare, se ia media a „n” puncte anterioare pentru a fi valoarea prognozată.

- Medie mobilă ponderată : O medie mobilă ponderată este o medie mobilă în care cele „n” valori anterioare au ponderi diferite.

- Netezire exponențială simplă: În această tehnică, se atribuie ponderi mai mari observațiilor mai recente decât observațiilor din trecutul îndepărtat.

- Modelul de tendință liniară al lui Holt: Această metodă ia în considerare tendința setului de date. Prin tendință, se înțelege natura crescătoare sau descrescătoare a seriei. Să presupunem că numărul de rezervări la un hotel crește în fiecare an, atunci putem spune că numărul de rezervări prezintă o tendință de creștere. Funcția de prognoză în această metodă este o funcție de nivel și tendință.

- Metoda Holt Winters: Acest algoritm ia în considerare atât tendința, cât și sezonalitatea seriei. De exemplu – numărul de rezervări într-un hotel este ridicat în weekend & scăzut în zilele lucrătoare și crește în fiecare an; există o sezonalitate săptămânală și o tendință de creștere.

- ARIMA: ARIMA este o tehnică foarte populară pentru modelarea seriilor temporale. Ea descrie corelația dintre punctele de date și ia în considerare diferența dintre valori. O îmbunătățire față de ARIMA este SARIMA (sau ARIMA sezonier). Vom analiza ARIMA puțin mai detaliat în secțiunea următoare.
Introducere la ARIMA
În această secțiune vom face o introducere rapidă în ARIMA, care va fi utilă pentru a înțelege Auto Arima. O explicație detaliată a Arima, a parametrilor (p,q,d), a graficelor (ACF PACF) și a implementării este inclusă în acest articol : Complete tutorial to Time Series.
ARIMA este o metodă statistică foarte populară pentru prognoza seriilor temporale. ARIMA înseamnă Auto-Regressive Integrated Moving Averages (medii mobile integrate autoregresive). Modelele ARIMA funcționează pe baza următoarelor ipoteze –
- Seria de date este staționară, ceea ce înseamnă că media și varianța nu trebuie să varieze în timp. O serie poate fi făcută staționară prin utilizarea transformării logaritmice sau prin diferențierea seriei.
- Datele furnizate ca intrare trebuie să fie o serie univariată, deoarece arima utilizează valorile trecute pentru a prezice valorile viitoare.
ARIMA are trei componente – AR (termen autoregresiv), I (termen de diferențiere) și MA (termen de medie mobilă). Să înțelegem fiecare dintre aceste componente –
- Termenul AR se referă la valorile trecute utilizate pentru a prognoza următoarea valoare. Termenul AR este definit de parametrul „p” din arima. Valoarea lui ‘p’ este determinată cu ajutorul graficului PACF.
- Termenul MA este utilizat pentru a defini numărul de erori de prognoză din trecut utilizate pentru a prezice valorile viitoare. Parametrul „q” din arima reprezintă termenul MA. Graficul ACF este utilizat pentru a identifica valoarea corectă a lui ‘q’.
- Ordinea de diferențiere specifică numărul de ori de câte ori se efectuează operația de diferențiere asupra seriei pentru a o face staționară. Teste precum ADF și KPSS pot fi utilizate pentru a determina dacă seria este staționară și ajută la identificarea valorii d.
Pași pentru implementarea ARIMA
Pașii generali pentru implementarea unui model ARIMA sunt –
- Încărcați datele: Primul pas pentru construirea modelului este, bineînțeles, încărcarea setului de date
- Preprocesare: În funcție de setul de date, se vor defini etapele de preprocesare. Aceasta va include crearea de marcaje temporale, conversia dtipului coloanei dată/timp, transformarea seriilor în serii univariate, etc.
- Make series stationary: Pentru a satisface ipoteza, este necesar să se facă seria staționară. Aceasta ar include verificarea staționarității seriei și efectuarea transformărilor necesare
- Determinarea valorii lui d: Pentru a face seria staționară, numărul de ori de câte ori a fost efectuată operația de diferență va fi luat ca valoare d
- Crearea graficelor ACF și PACF: Acesta este cel mai important pas în implementarea ARIMA. Diagramele ACF PACF sunt utilizate pentru a determina parametrii de intrare pentru modelul nostru ARIMA
- Determinarea valorilor p și q: Citiți valorile lui p și q din graficele din etapa anterioară
- Adaptați modelul ARIMA: Utilizând datele procesate și valorile parametrilor pe care le-am calculat la etapele anterioare, ajustați modelul ARIMA
- Predict values on validation set: Prevedeți valorile viitoare
- Calculați RMSE: Pentru a verifica performanța modelului, verificați valoarea RMSE folosind predicțiile și valorile reale din setul de validare
De ce avem nevoie de Auto ARIMA?
Deși ARIMA este un model foarte puternic pentru prognozarea seriilor de date temporale, procesele de pregătire a datelor și de reglare a parametrilor sfârșesc prin a consuma foarte mult timp. Înainte de a implementa ARIMA, trebuie să faceți seria staționară și să determinați valorile lui p și q cu ajutorul graficelor pe care le-am discutat mai sus. Auto ARIMA ne simplifică foarte mult această sarcină, deoarece elimină pașii de la 3 la 6 pe care i-am văzut în secțiunea anterioară. Mai jos sunt pașii pe care trebuie să-i urmați pentru implementarea auto ARIMA:
- Încărcați datele: Acest pas va fi același. Încărcați datele în notebook-ul dumneavoastră
- Prelucrarea datelor: Datele de intrare trebuie să fie univariate, prin urmare renunțați la celelalte coloane
- Fit Auto ARIMA: Fit the model on the univariate series
- Predict values on validation set: Efectuați predicții pe setul de validare
- Calculați RMSE: Verificați performanța modelului folosind valorile prezise față de valorile reale
Am ocolit complet selecția caracteristicilor p și q, după cum puteți vedea. Ce ușurare! În secțiunea următoare, vom implementa auto ARIMA folosind un set de date de jucărie.
Implementare în Python și R
Vom folosi setul de date International-Air-Passenger. Acest set de date conține totalul lunar al numărului de pasageri (în mii). Acesta are două coloane – luna și numărul de pasageri. Puteți descărca setul de date de la acest link.
#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)
output -76.51355764316357
Mai jos este codul R pentru aceeași problemă:
# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)
Cum selectează Auto Arima cei mai buni parametri
În codul de mai sus, am folosit pur și simplu .fit() pentru a ajusta modelul fără a fi nevoie să selectăm combinația de p, q, d. Dar cum și-a dat seama modelul care este cea mai bună combinație a acestor parametri? Auto ARIMA ia în considerare valorile AIC și BIC generate (după cum puteți vedea în cod) pentru a determina cea mai bună combinație de parametri. Valorile AIC (Akaike Information Criterion) și BIC (Bayesian Information Criterion) sunt estimatori pentru a compara modelele. Cu cât aceste valori sunt mai mici, cu atât modelul este mai bun.
Consultați aceste linkuri dacă vă interesează matematica din spatele AIC și BIC.
Note de final și lecturi suplimentare
Am constatat că auto ARIMA este cea mai simplă tehnică pentru realizarea previziunilor seriilor temporale. Cunoașterea unei scurtături este bună, dar să fii familiarizat cu matematica din spatele ei este, de asemenea, important. În acest articol am trecut în revistă detaliile despre cum funcționează ARIMA, dar asigurați-vă că parcurgeți linkurile furnizate în articol. Pentru o referință ușoară, iată din nou link-urile:
- Un ghid complet pentru începători pentru prognoza seriilor temporale în Python
- Tutorial complet pentru serii temporale în R
- 7 tehnici de prognoză a seriilor temporale (cu coduri python)
Vă sugerez să exersați ceea ce am învățat aici pe această problemă practică: Time Series Practice Problem. Puteți, de asemenea, să urmați cursul nostru de instruire creat pe aceeași problemă practică, Time series forecasting, pentru a vă oferi un avans.
.