Vom descrie trei exemple din domeniul științelor vieții: unul din fizică, unul legat de genetică și unul dintr-un experiment cu șoareci. Acestea sunt foarte diferite, însă vom ajunge să folosim aceeași tehnică statistică: ajustarea modelelor liniare. Modelele liniare sunt de obicei predate și descrise în limbajul algebrei matriciale.
Exemple motivante
Obiecte în cădere
Imaginați-vă că sunteți Galileo în secolul al XVI-lea, încercând să descrieți viteza unui obiect în cădere. Un asistent urcă pe Turnul din Pisa și lasă să cadă o bilă, în timp ce alți câțiva asistenți înregistrează poziția la momente diferite. Să simulăm niște date folosind ecuațiile pe care le cunoaștem astăzi și adăugând unele erori de măsurare:
set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##metersAsistenții îi înmânează datele lui Galileo și iată ce vede el:
mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")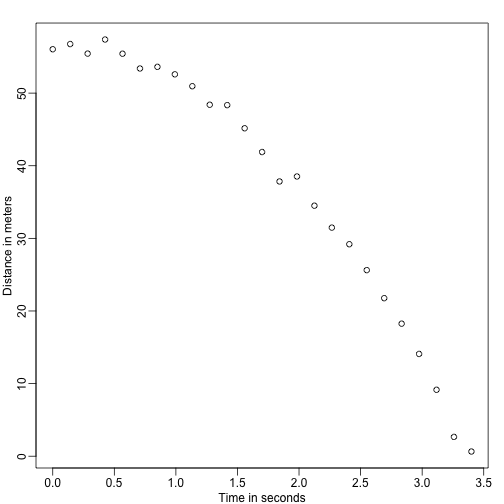
Nu cunoaște ecuația exactă, dar uitându-se la graficul de mai sus, deduce că poziția ar trebui să urmeze o parabolă. Astfel, el modelează datele cu:
Cu reprezentând locația, reprezentând timpul și ținând cont de eroarea de măsurare. Acesta este un model liniar deoarece este o combinație liniară a unor cantități cunoscute (th s) denumite predictori sau covariate și a unor parametri necunoscuți (the s).
Tatăl &înălțimea fiului
Imaginați-vă acum că sunteți Francis Galton în secolul al XIX-lea și colectați date de înălțime împerecheate de la tați și fii. Bănuiți că înălțimea se moștenește. Datele dvs.:
library(UsingR)x=father.son$fheighty=father.son$sheightaspectul este următorul:
plot(x,y,xlab="Father's height",ylab="Son's height")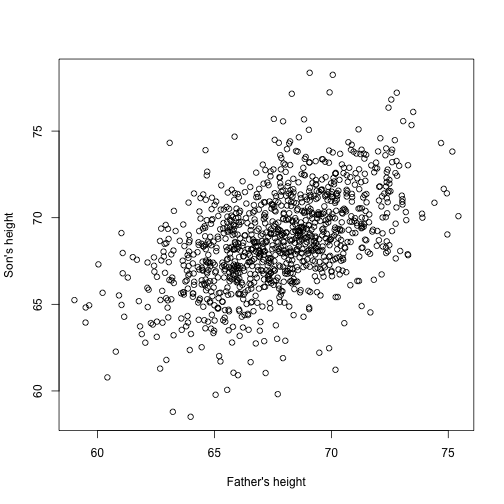
Înălțimea fiilor pare să crească liniar cu înălțimea taților. În acest caz, un model care descrie datele este următorul:
Acesta este, de asemenea, un model liniar cu și , înălțimile tatălui și, respectiv, a fiului, pentru a -lea pereche și un termen care să țină cont de variabilitatea suplimentară. Aici ne gândim la înălțimea taților ca predictor și ca fiind fixă (nu aleatorie), așa că folosim litere mici. Eroarea de măsurare singură nu poate explica toată variabilitatea observată în . Acest lucru are sens deoarece există și alte variabile care nu se regăsesc în model, de exemplu, înălțimile mamelor, hazardul genetic și factorii de mediu.
Eșantioane aleatorii din mai multe populații
Aici citim date privind greutatea corporală a șoarecilor care au fost hrăniți cu două diete diferite: cu conținut ridicat de grăsimi și de control (chow). Avem un eșantion aleatoriu de 12 șoareci pentru fiecare. Suntem interesați să determinăm dacă dieta are un efect asupra greutății. Iată datele:
dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")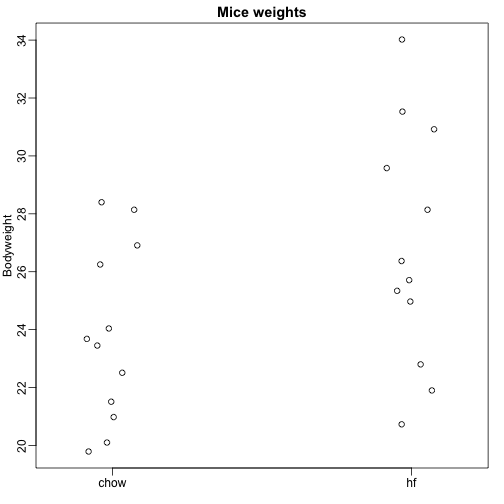
Vrem să estimăm diferența de greutate medie între populații. Am demonstrat cum să facem acest lucru folosind teste t și intervale de încredere, pe baza diferenței dintre mediile eșantioanelor. Putem obține exact aceleași rezultate folosind un model liniar:
cu greutatea medie din dieta chow, diferența dintre medii, când șoarecele primește dieta bogată în grăsimi (hf), când primește dieta chow și explică diferențele dintre șoarecii din aceeași populație.
Modele liniare în general
Am văzut trei exemple foarte diferite în care se pot folosi modele liniare. Un model general care înglobează toate exemplele de mai sus este următorul:
Rețineți că avem un număr general de predictori . Algebra matricială oferă un limbaj compact și un cadru matematic pentru a calcula și a face derivări cu orice model liniar care se încadrează în cadrul de mai sus.
Stimarea parametrilor
Pentru ca modelele de mai sus să fie utile trebuie să estimăm necunoscutele s. În primul exemplu, dorim să descriem un proces fizic pentru care nu putem avea parametri necunoscuți. În al doilea exemplu, înțelegem mai bine moștenirea prin estimarea cât de mult, în medie, înălțimea tatălui afectează înălțimea fiului. În exemplul final, dorim să determinăm dacă există, de fapt, o diferență: dacă .
Abordarea standard în știință este de a găsi valorile care minimizează distanța dintre modelul ajustat și date. Ceea ce urmează se numește ecuația celor mai mici pătrate (LS) și o vom vedea adesea în acest capitol:
După ce găsim minimul, vom numi valorile estimările celor mai mici pătrate (LSE) și le vom nota cu . Cantitatea obținută atunci când se evaluează ecuația celor mai mici pătrate la estimări se numește sumă reziduală a pătratelor (RSS). Deoarece toate aceste cantități depind de , ele sunt variabile aleatoare. S sunt variabile aleatoare și, în cele din urmă, vom efectua inferențe asupra lor.
Exemplu de obiect în cădere revizuit
Grație profesorului meu de fizică din liceu, știu că ecuația traiectoriei unui obiect în cădere este:
cu și înălțimea și, respectiv, viteza de pornire. Datele pe care le-am simulat mai sus au urmat această ecuație și au adăugat eroarea de măsurare pentru a simula n observațiile pentru aruncarea mingii din turnul din Pisa . Acesta este motivul pentru care am folosit acest cod pentru a simula datele:
g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)Iată cum arată datele cu linia continuă reprezentând traiectoria adevărată:
plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)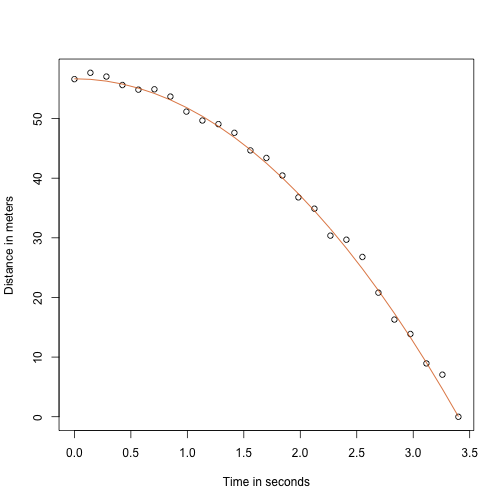
Dar ne-am prefăcut că suntem Galileo și deci nu cunoaștem parametrii din model. Datele sugerează că este o parabolă, așa că o modelăm ca atare:
Cum găsim LSE?
Funcția lm
În R putem ajusta acest model prin simpla utilizare a funcției lm. Vom descrie această funcție în detaliu mai târziu, dar iată o previzualizare:
tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17Ne oferă LSE, precum și erori standard și valori p.
O parte din ceea ce facem în această secțiune este să explicăm matematica din spatele acestei funcții.
Stimarea celor mai mici pătrate (LSE)
Să scriem o funcție care calculează RSS pentru orice vector :
rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}Acum, pentru orice vector tridimensional, obținem un RSS. Iată o reprezentare grafică a RSS în funcție de momentul în care le menținem fixe pe celelalte două:
Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)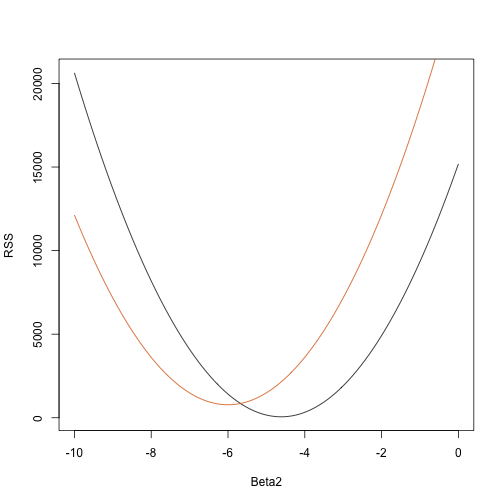
Încercarea și eroarea aici nu va funcționa. În schimb, putem folosi calculul: să luăm derivatele parțiale, să le fixăm la 0 și să rezolvăm. Desigur, dacă avem mulți parametri, aceste ecuații pot deveni destul de complexe. Algebra liniară oferă o modalitate compactă și generală de rezolvare a acestei probleme.
Mai multe despre Galton (Avansat)
Când a studiat datele tată-fiu, Galton a făcut o descoperire fascinantă folosind analiza exploratorie.
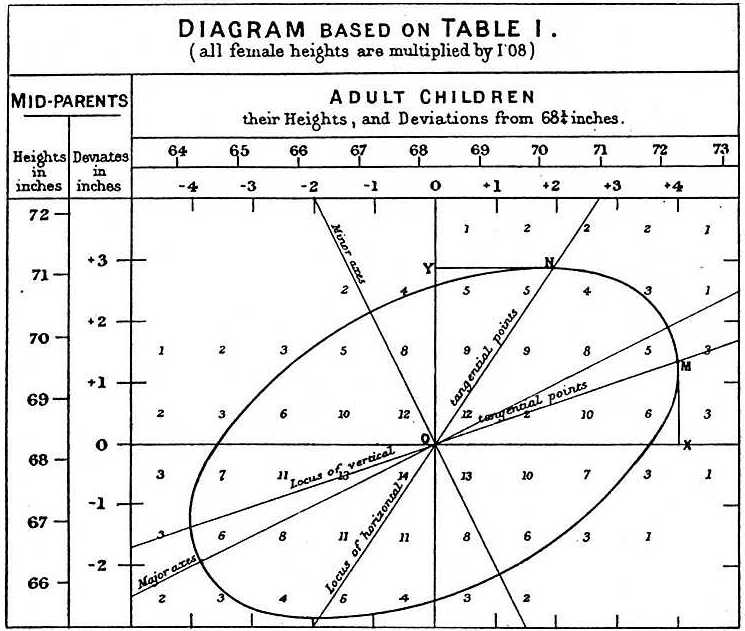
El a observat că, dacă a tabelat numărul de perechi de înălțime tată-fiu și a urmărit toate valorile x,y care au aceleași totaluri în tabel, acestea formează o elipsă. În graficul de mai sus, realizat de Galton, se vede elipsa formată de perechile care au 3 cazuri. Acest lucru a dus apoi la modelarea acestor date ca o normală bivariată corelată pe care am descris-o mai devreme:
Am descris cum putem folosi matematica pentru a arăta că dacă se menține fixă (condiția să fie ) distribuția lui este distribuită normal cu media: și abaterea standard . Observați că este corelația dintre și , ceea ce implică faptul că dacă fixăm , urmează de fapt un model liniar. Parametrii și din modelul nostru liniar simplu pot fi exprimați în termeni de , și .
.