Existe simetria do ponto quando a figura é desenhada em torno de um único ponto.

Este ponto é chamado de centro da figura ou o centro da simetria. Na figura adjacente, observamos que correspondente ao ponto X da figura, existe um ponto X’ do outro lado do centro que é diretamente oposto a X e está sobre a figura. Dizemos que a figura é simetria sobre o centro.
Nota:
Quando giramos uma figura cerca de 180° e ela recupera sua forma original,então dizemos que existe simetria de pontos na figura.
Exemplos das figuras exibindo simetria de pontos:
● Todas as letras do alfabeto inglês.
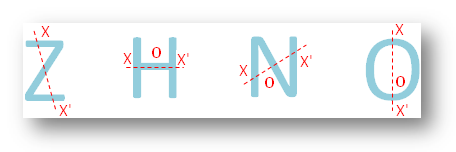
● Diferentes figuras geométricas.
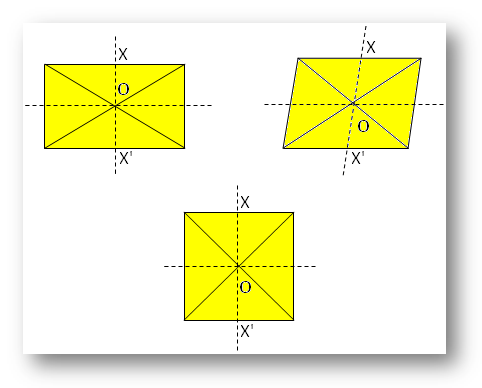
Nota:
Aqui, O é o centro de simetria.
Com respeito a X existe X’, de tal forma que X’ é directamente oposto a X do outro lado de O.
Quais são as condições que uma forma ou figura satisfaz para a simetria de pontos?
As condições que uma forma ou figura satisfaz para a simetria de pontos, ou seja, cada parte deve ter uma parte correspondente
– a distância deve ser igual ao ponto central
– mas deve estar na direcção oposta.
● Conceitos Relacionados
● Simetria Linear
● Linhas de Simetria
● Simetria Rotacional
● Ordem da Simetria Rotacional
● Tipos de Simetria
● Reflexão
● Reflexão de um Ponto em x-eixo
● Reflexão de um Ponto em y-eixo
>
● Reflexão de um ponto na origem
● Rotação
● 90 Graus Rotação no sentido horário
● 90 Graus Rotação no sentido anti-horário
● 180 Graus Rotação
>Problemas Matemáticos do 7º Grau
Prática Matemática do 8º Grau
Da Simetria Pontual à PÁGINA INICIAL