Qual é a permeabilidade da membrana celular?
Modo Leitor
Uma das características da assinatura de todos os organismos vivos é que eles contêm uma mistura distinta de iões e pequenas moléculas. A composição não só difere do ambiente, mas também pode variar dentro da célula. Por exemplo, a concentração de íons hidrogênio em alguns compartimentos celulares pode ser 104 vezes maior do que em outros (as mitocôndrias atingindo um pH tão alto quanto 8; os lisossomos com um pH tão baixo quanto 4, BNID 107521, 106074). A razão das concentrações de íons Ca2+ nos compartimentos de fluido extra e intracelular pode ser novamente 104 vezes maior (BNID 104083). Esta diferença de concentração é tão grande que o transporte de um íon Ca2+ através da membrana, do compartimento intra e extracelular, requer a energia de mais de um próton ou íon de sódio fluindo pelo gradiente de força próton-motiva. Para ver isso, o leitor deve se lembrar da regra geral dos nossos truques da lista de comércio que para estabelecer uma ordem de magnitude de diferença potencial requer 6 kJ/mol (≈2 kBT). Esta energia pode ser obtida, por exemplo, pelo transporte de uma carga elétrica através de uma diferença de potencial de 60 mV. Para alcançar quatro ordens de magnitude de concentração seria então necessária uma carga para percorrer cerca de 240 mV de força motriz dos elétrons (na verdade ainda mais devido à dupla carga do íon de cálcio). Isto está muito próximo da tensão de ruptura da membrana, conforme discutido na vinheta “Qual é a diferença de potencial elétrico entre as membranas? De fato, a alta taxa de concentração de Ca2+ é geralmente obtida através do acoplamento ao transporte de três íons sódio ou à hidrólise de ATP, o que ajuda a alcançar a diferença de densidade necessária sem energizar perigosamente a membrana.
A segunda lei da termodinâmica nos ensina que, em geral, a presença de gradientes de concentração acabará sendo sangrada por processos de transporte de massa, que conduzem os sistemas a um estado de equilíbrio. Entretanto, embora a segunda lei da termodinâmica nos diga a natureza do estado final de um sistema (por exemplo, concentrações uniformes), ela não nos diz quanto tempo levará para atingir esse estado. As membranas evoluíram para formar uma barreira muito eficaz para a transferência espontânea de muitas espécies iônicas e moleculares. Para estimar a escala de tempo para equalizar concentrações, precisamos conhecer as taxas de transporte de massa, que dependem de propriedades chave dos materiais como constantes de difusão e permeabilidade.
Uma classe de “leis” de grande sucesso, que descrevem o comportamento de sistemas que sofreram algum pequeno desvio do equilíbrio, são as leis de transporte linear. Estas leis apresentam uma relação linear simples entre a taxa de transporte de alguma quantidade de interesse e a força motriz associada. Para o transporte de massa, existe uma relação linear entre o fluxo (isto é, o número de moléculas que atravessam área unitária por unidade de tempo) e a diferença de concentração (que serve como a força motriz relevante). Para o transporte através das membranas, estas ideias foram codificadas na equação simples (para soluto neutro) j= – p-(cin-cout), onde j é o fluxo líquido para a célula, cin e cout referem-se às concentrações no interior e exterior da região ligada à membrana, e p é um parâmetro material conhecido como a permeabilidade. As unidades de p podem ser deduzidas observando-se que o fluxo tem unidades de número/(área x tempo) e a concentração tem unidades de número/volume, o que implica que as unidades de p em si são comprimento/tempo. Como muitas quantidades de transporte (por exemplo, condutividades elétricas de materiais que abrangem mais de 30 ordens de magnitude), a permeabilidade tem uma faixa dinâmica muito grande, como ilustrado na Figura 1. Como visto na figura, as camadas lipídicas têm uma gama de permeabilidades de quase 1010 vezes.
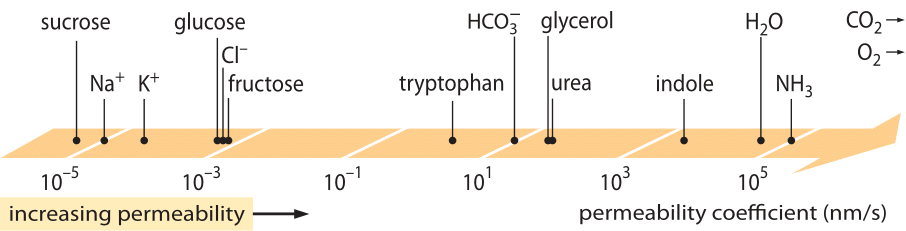
Figure 1: A ampla gama de permeabilidades das membranas de diferentes compostos na célula. As membranas são mais permeáveis a compostos não carregados e menos permeáveis a íons carregados. Note que a existência de canais de íons fará com que a permeabilidade aparente quando eles são abertos várias ordens de magnitude seja maior. As unidades são escolhidas como nm/s e vários nm é a largura característica da membrana. Figura adaptada de R. N. Robertson, The Lively Membranes, Cambridge University Press, 1983. O valor para glicose é menor do que em Robertson baseado em várias fontes como BNID 110830, 110807. Outras fontes de dados: BNID 110729, 110731, 110816, 110824, 110806.
Que parâmetros físico-químicos guiam a localização de um composto nesta escala de permeabilidades? Uma regra geral é que moléculas pequenas têm permeabilidades maiores do que moléculas maiores. Outra regra geral é que compostos neutros podem atravessar a membrana muitas ordens de magnitude mais rapidamente do que compostos carregados similares. Entre os compostos carregados, os compostos negativos (aniônicos) tendem a ter permeabilidades muito mais altas do que os compostos positivos (catiônicos). A chamada regra Overton afirma que a permeabilidade da membrana aumenta com a hidrofobicidade, onde a hidrofobicidade é a tendência de um composto a preferir um solvente não polar a um solvente polar (aquoso). A regra Overton prevê que moléculas carregadas (não hidrofóbicas), tais como íons, tenderão a ter baixa permeabilidade, pois incorrerão em uma penalidade energética associada à penetração da membrana, enquanto gases dissolvidos, tais como O2 e CO2, que são hidrofóbicos (pois são descarregados e simétricos), terão alta permeabilidade. De fato, a permeabilidade das membranas de bílis lipídicos ao CO2 dão valores que são 0,01-1 cm/s (sim, as medidas de permeabilidade têm incertezas muito altas entre diferentes laboratórios, BNID 110004, 110617, 102624), maiores que todos os outros valores mostrados na Figura 1. Este valor mostra que a barreira criada pela membrana celular é na verdade menos um obstáculo do que a barreira causada pela camada não agitada de água que envolve a membrana celular do exterior. Tal inferência pode ser derivada pela equação do coeficiente de permeabilidade de um obstáculo, dado por p=K x D/l onde l é a largura, D o coeficiente de difusão e K o coeficiente de partição entre o meio e o material do obstáculo. Isto também é conhecido como o modelo de “solubilidade-difusão” para permeabilidade onde estes denotam os efeitos K e D que são dois passos que afectam a permeabilidade. Para uma camada não agitada de água K=1 por ser muito semelhante ao meio, mas para uma membrana o valor para todos, excepto o material mais hidrofóbico, é geralmente várias ordens de magnitude inferior a 1. Esta dependência de K está no centro da regra Overton acima mencionada. A alta permeabilidade ao CO2 também sugere que canais como aquaporinas que foram sugeridos para servir para o transporte de gás para a célula não são necessários, já que a membrana é suficientemente permeável. Para ver como as propriedades das membranas afetam a composição química dos metabólitos, vamos recorrer ao cálculo do tempo de vazamento para diferentes compostos
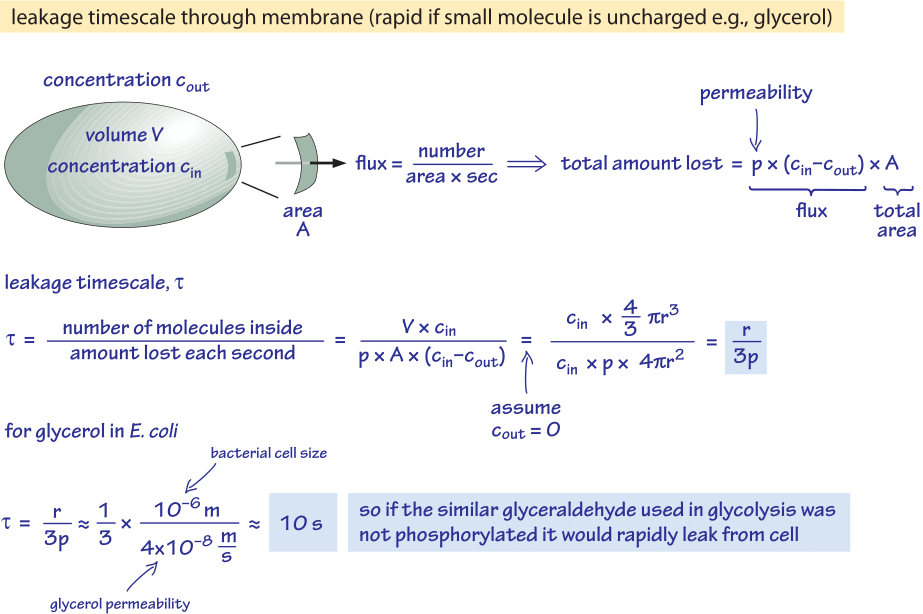
Figure 2: Cálculo da parte de trás do envelope do tempo para a molécula de glicose não-fosforilada se difundir passivamente para fora de uma célula bacteriana. As implicações funcionais são então consideradas para células de crescimento rápido onde o efeito é insignificante e para células em estado estacionário onde pode causar uma fuga apreciável de recursos.
Consideramos o glicerol, por exemplo. A análise mostrada na Figura 2 dá uma estimativa para o tempo do seu vazamento para fora da célula se a molécula não for fosforilada ou convertida em uma forma mais hidrofílica. A permeabilidade da membrana celular ao glicerol é p≈10-100 nm/s (BNID 110824), como pode ser lido na Figura 1. A escala de tempo para uma molécula de glicerol dentro da célula escapar de volta para o meio circundante, assumindo que não há fluxo de retorno para a célula (cout=0), pode ser crudamente estimada observando-se que o efluxo da célula é p-A-cin onde A é a área de superfície da célula. A escala de tempo é encontrada tomando a quantidade total na célula, V-cin (onde V é o volume da célula ou mais precisamente o volume de água da célula), e dividindo por este fluxo resultante para uma célula bacteriana (r≈1 μm) numa escala de tempo:
t =V-cin/p-A-cin =(4πr2/3)/(4πr2-3×10-6 cm/s) ≈ 10 s.
Esta é uma estimativa grosseira porque não contabilizamos a diminuição da concentração de cin com o tempo que dará um fator de correção de 1/ln(2), ou seja, menos de 2 dobras de aumento. O que aprendemos com essas estimativas é que se os intermediários glicolíticos glicolíticos gliceraldeído ou diidroxiacetona, que são muito semelhantes à glicerol, não fossem fosforilados, resultando na adição de uma carga, eles seriam perdidos para o meio por difusão através da membrana celular. Em meios de laboratório, onde uma fonte de carbono é fornecida em abundância, esta não é uma questão importante, mas em um ambiente natural onde as células estão frequentemente esperando em fase estacionária por uma pulsação de nutrientes (E. acredita-se que a coli passa por meses sem crescimento após sua excreção do corpo antes de encontrar um novo hospedeiro), a célula pode conter suas perdas, certificando-se de que os intermediários metabólicos sejam marcados com uma carga que os impeça de recrutar a barreira apresentada pelo bocal lipídico.




