Se você gosta de uma bebida, então uma garrafa de Klein não é um recipiente recomendado. Pode parecer-se vagamente com uma garrafa, mas não encerra nenhum volume, o que significa que não pode realmente segurar nenhum líquido. O que quer que você despeje “dentro” vai voltar a sair.
Como você constrói uma coisa tão estranha e por que você iria querer construí-la? O matemático Felix Klein, que descobriu a garrafa em 1882, descreveu-a como uma superfície que “pode ser visualizada invertendo um pedaço de um tubo de borracha e deixando-a passar por si mesma para que o exterior e o interior se encontrem”.
O seu navegador não suporta a etiqueta de vídeo.link directo
É óbvio que a garrafa Klein, tal como a esfera mais familiar, é uma superfície fechada: é finita no sentido em que se pode encaixar numa região finita do espaço, mas uma formiga pode andar sobre ela para sempre sem nunca encontrar um limite ou cair sobre uma borda. Ao contrário da esfera, que tem um interior e um exterior, a garrafa de Klein é unilateral: andando em volta, a nossa formiga poderia alcançar ambos os lados de cada ponto da superfície. É por isso que a garrafa não tem volume, e também responde à pergunta “porquê”: a garrafa de Klein é interessante porque não encontramos muitas formas unilaterais na natureza. (Veja aqui outra imagem muito bonita de uma garrafa de Klein.)

A tira Möbius é unilateral – veja a versão animada. (Imagem e animação de Konrad Polthier.)
Se isto é um pouco confuso, pense num exemplo mais simples de uma superfície unilateral: a famosa tira de Möbius. Você pode fazer uma pegando duas pontas de uma tira de papel, dando um giro à tira, e depois colando as pontas juntas. Usando uma tira de papel cujos dois lados têm cores diferentes, digamos verde e laranja, é fácil convencer-se de que a tira Möbius resultante é unilateral. Uma vez que você tenha torcido e colado, você verá que pode alcançar cada ponto laranja de cada ponto verde sem ter que furar o papel ou subir por cima da borda.
Não como a garrafa Klein, a tira Möbius tem um limite – ela é feita das duas bordas não coladas da tira original. Mas há uma ligação entre as duas. Se você pegar duas tiras de Möbius e criar uma forma fechada unindo seus limites usando uma tira de duas faces comum, como mostrado abaixo, o que você obtém é exatamente a garrafa de Klein.
Seu navegador não suporta a etiqueta de vídeo.link direto
banda cujos lados anterior e posterior são coloridos de branco e azul respectivamente. Animação de Konrad Polthier.
Este facto inspirou o matemático Leo Moser a compor um limerick:
Um matemático chamado KleinThought the Möbius band was divine.Said he: “Se colares as bordas de dois, vais ter uma garrafa estranha como a minha.”
Alguns matemáticos são mesmo multi-talentosos!
Outra característica curiosa da garrafa de Klein é que se intercepta a si própria, o que significa que é difícil de fazer a partir de um único tubo de borracha como Klein sugeriu. A rigor, o objecto auto-intersectante descrito acima não é uma garrafa de Klein, mas (como Klein indicou) apenas a visualização de uma. Para entender porquê, pense primeiro no donut mais familiar (conhecido matematicamente como um toro). Você pode fazer um toro a partir de uma folha quadrada de borracha, primeiro colando dois lados opostos para formar um cilindro, e depois colando os dois componentes de contorno desse cilindro para obter o toro.

Fazer um toro: Primeiro colar pontos opostos em dois lados opostos do quadrado para fazer um cilindro e depois colar os dois círculos de delimitação desse cilindro (correspondendo à colagem de pontos opostos nos dois lados restantes do quadrado) para formar um toro.
Se não se quiser incomodar com a colagem, basta pensar no toro como um quadrado, tendo em conta que pontos opostos em lados opostos são considerados iguais. Assim, quando você desliza uma forma desenhada no “quadrado” através da borda superior, ele irá reaparecer na borda inferior e quando você deslizá-lo sobre a borda direita ele irá reaparecer na borda esquerda (e vice-versa).
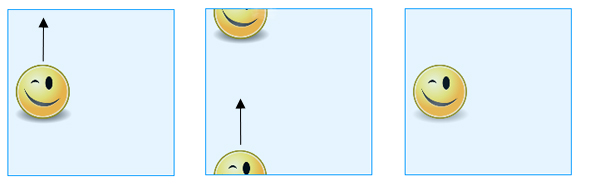
Quando você desliza uma forma desenhada no “quadrado” através da borda superior, ela irá reaparecer na borda inferior.
Para obter uma verdadeira garrafa de Klein, comece da mesma forma, identificando pontos opostos em um par de lados opostos de um quadrado. Para o outro par de lados, porém, não identifique pontos que são diretamente opostos, mas pontos que são diagonalmente opostos, como mostrado na figura.
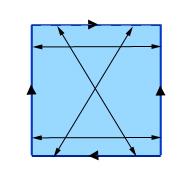
Fazer uma garrafa de Klein: identifique pontos opostos de dois lados opostos (os verticais nesta figura) e depois identifique pontos diagonalmente opostos nos dois lados restantes. (Se você rotular pontos nos lados superior e inferior da esquerda para a direita pelos números 0 a 1, então um ponto com rótulo x no lado superior é identificado com o ponto com rótulo 1-x no lado inferior.)
O objeto resultante é a garrafa de Klein. Novamente, você pode pensar nele como um quadrado, tendo em mente quais pontos de limite são considerados iguais. Se você deslizar uma forma sobre uma das bordas que tinha pontos opostos identificados (vertical em nossa figura), ela reaparece no lado oposto, como antes. Se, no entanto, deslizarmos sobre uma das arestas cujos pontos foram identificados na diagonal (horizontal na nossa imagem), ela aparece no lado oposto, mas deslocada e como uma imagem espelho do seu eu original.
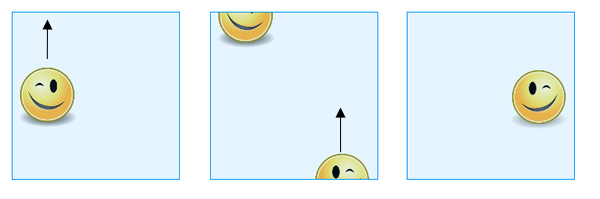
Se você deslizar uma forma sobre a borda superior, ela aparece sobre a borda inferior, mas sobre o outro lado e como uma imagem espelho do seu eu original.
A única maneira de construir esta forma no espaço tridimensional, realmente colando pontos juntos, é permitir que ela se intercepte. Isto equivale a identificar pares de pontos no interior do quadrado original, pelo que, a rigor, a forma resultante não é exactamente a mesma que a garrafa de Klein, que apenas tem pontos de contorno identificados. É apenas uma forma de representar a garrafa no espaço tridimensional (existem outras também).
O seu browser não suporta a etiqueta de vídeo. Link directo
Mirror image and orientability. Animação de Konrad Polthier.
Curiamente, os conceitos de “dentro”, “fora” e “unilateralidade” dependem do espaço ambiente em que um objeto está sentado. Por exemplo, um laço desenhado num pedaço de papel (no espaço bidimensional) tem um bem definido dentro e fora, mas um laço desenhado no espaço tridimensional não tem. É por isso que não podemos falar de unilateralidade, a menos que primeiro decidamos como incorporar uma superfície no espaço tridimensional. Existe, contudo, uma propriedade intimamente relacionada que é intrínseca a uma forma e não depende do espaço circundante. Uma superfície é chamada orientável se você não puder deslizar uma forma desenhada sobre ela e voltar para onde ela começou, de modo que ela se pareça com sua própria imagem espelhada. Como você pode ver na animação que acompanha a imagem à direita, a faixa Möbius não é orientável. E como você pode ver na imagem com a cara sorridente acima, a garrafa de Klein também não é. Para dar-lhe a sua descrição matemática completa, a garrafa de Klein é uma superfície fechada e não orientável. Para saber mais sobre ela, veja o artigo Dentro da garrafa de Klein.
Sobre o autor
Marianne Freiberger é editora da Plus.