Construir Triângulo Equilateral – MathBitsNotebook (Geo

Utilizar apenas a bússola e a borda reta ao desenhar uma construção. Sem desenho à mão livre!

Faremos TRÊS construções de um triângulo equilátero. A primeira será construir um triângulo equilátero dado o comprimento de um lado, e as outras duas serão construir um triângulo equilátero inscrito em um círculo.

Dado: o comprimento de um lado do triângulo Construir: um triângulo equilátero

STEPS:
1. Coloque o ponto da bússola em A e meça a distância ao ponto B. Balance um arco deste tamanho acima (ou abaixo) do segmento.
2. Sem alterar o vão na bússola, coloque o ponto da bússola em B e balance o mesmo arco, intersectando com o primeiro arco.
3. Marcar o ponto de intersecção como o terceiro vértice do triângulo equilátero.

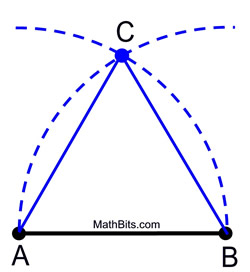>	Ver os círculos completos em trabalho.

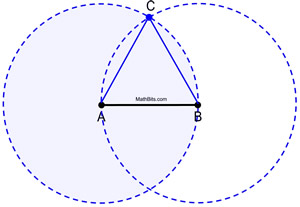Comprovante de Construção: O círculo A é congruente ao círculo B, já que cada um deles foi formado usando o mesmo comprimento de raio, AB. Como AB e AC são comprimentos de raios do círculo A, eles são iguais um ao outro. Da mesma forma, AB e BC são raios do círculo B, e são iguais um ao outro. Portanto, AB = AC = BC por substituição (ou propriedade transitiva). Como segmentos congruentes têm comprimentos iguais, e ΔABC é equilátero (tendo três lados congruentes).

STEPS:
1. Coloque o seu ponto de bússola no papel e desenhe um círculo. (Mantenha este intervalo de bússola!)
2. Coloque um ponto, rotulado como A, em qualquer parte da circunferência do círculo para agir como um ponto de partida.
3. Sem alterar o vão da bússola, coloque o ponto da bússola em A e balance um pequeno arco atravessando a circunferência da circunferência.
4. Sem alterar o vão da bússola, mova o ponto da bússola para a intersecção do arco anterior com a circunferência e faça outro pequeno arco na circunferência da circunferência.
5. Continue repetindo este processo de “passo” ao redor da circunferência até retornar ao ponto A.
6. Começando em A, conecte todos os outros arcos da circunferência para formar o triângulo equilátero.

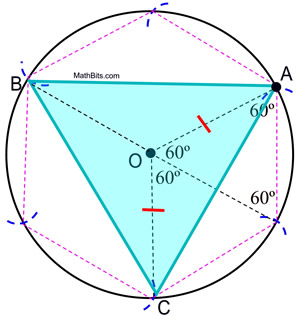Consulte a prova de um hexágono regular inscrito para mais informações relativas à prova desta construção.

Prova de construção: A prova do hexágono regular inscrito mostra que os ângulos centrais de um hexágono regular contêm 60º. Os ângulos centrais do triângulo inscrito neste círculo contêm 120º. Como ΔAOC é isósceles (OA e OC são comprimentos de raios), m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC ΔCOB ΔBOA por SAS. Por CPCTC, ∠OCB ∠OCA e m∠OCB = 30º por substituição e m∠BCA = 60º. De forma semelhante, temos m∠ACB = m∠CBA = m∠BAC = 60º e equilátero ΔABC.

PASSOS:
1. Coloque o ponto da bússola no papel e desenhe um círculo, O. (Mantenha este vão da bússola!)
2. Usando uma reta, desenhe um diâmetro do círculo, etiquetando os pontos finais P e B.
3. Sem mudar o vão da bússola, coloque o ponto da bússola em P e desenhe um círculo completo.
4. Etiquete os pontos de intersecção das duas circunferências circulares com A e C.
5. Desenhar segmentos de A a B, B a C e C a A, para formar o triângulo equilátero.

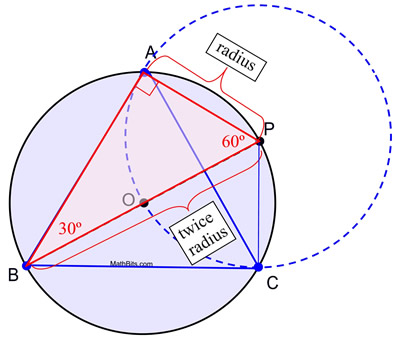
Prova de Construção: Esta construção usa o facto de que um ângulo inscrito num semicírculo é um ângulo recto, e que num triângulo de 30º-60º-90º, o comprimento da perna curta é metade do comprimento da hipotenusa. Nesta construção, o círculo O e o círculo P são congruentes uma vez que têm o mesmo comprimento de raio. AP é um raio de comprimento do círculo P e raios AP = OP. OP é também um raio de comprimento do círculo O (juntamente com OB) e diâmetro BP = BO + OP = 2 OP. Por substituição, BP = 2 AP, criando as condições necessárias para m∠ABP = 30º. Consequentemente, m∠APB = 60º. Um argumento semelhante pode ser usado para estabelecer que para ΔPBC, m∠PBC = 30º e m∠BPC = 60º fazendo ΔPBC ΔPBA por ASA (com lado compartilhado de B a P).
Agora, já que são os lados correspondentes dos dois triângulos congruentes, fazendo ΔABC isósceles. ∠BAC ∠BCA já que os ângulos de base de um triângulo isósceles são congruentes.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º por Angle Addition Postulate e substituição. m∠BAC + m∠BCA + m∠ABC = 180º porque a soma dos ângulos medidos em um triângulo é de 180º. Como m∠BAC + m∠BAC + 60º = 180º por substituição, sabemos 2m∠BAC = 120º e m∠BAC = 60º. Consequentemente m∠BCA também é igual a 60º por substituição, fazendo ΔABC equilateral.