Antes de começarmos temos de fazer algumas suposições.
Primeiro, estamos a trabalhar com fluidos Newtonianos. Esta é a forma matemática mais simples de contabilizar a viscosidade de um fluido. Não há fluidos reais que se enquadram perfeitamente nesta categoria, mas na maioria dos casos, ar e água podem ser tratados como um fluido newtoniano. A outra hipótese muito importante que estamos a fazer é que o fluido é incompressível. Isto significa que sua densidade, rho, é uma constante.
Conservação de massa
A primeira equação nos diz que a massa do fluido em que estamos trabalhando é conservada. O fluido pode mudar a sua forma mas esta equação diz-nos que a massa é a mesma forma que começa a terminar.
Agora vamos falar de matemática. A letra u representa a velocidade do fluido e é um vector. Tem três componentes, podemos chamar-lhes u, v, w e representam a velocidade do fluido no sentido x, y, e z. A letra grega nabla ∇ seguida de um ponto é o operador de divergência. Isto significa que temos de diferenciar os seus componentes em todas as direcções (neste caso x, y, z).

A primeira derivada está a dizer-nos como o componente x da velocidade está a mudar à medida que nos deslocamos no sentido x. O mesmo é válido para as outras duas derivadas. Como esta equação é igual a zero, ela está nos mostrando que a massa é conservada.
Conservação do momento

A segunda equação é na verdade um conjunto de três equações diferenciais. Esta é a que pode ser descrita como a segunda lei de Newton para os fluidos. Se expandirmos a expressão obtemos um sistema complexo.
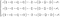
Desde que é muito mais simples de compreender, vamos concentrar-nos na conservação do momento não expandido.
Quando trabalhamos com fluidos podemos dizer que massa e densidade são as mesmas coisas (desde que o seu volume seja o mesmo). Se estamos considerando dois fluidos, podemos dizer que o mais denso é o mais “pesado” (por exemplo, mercúrio e água). Neste caso, a letra grega ρ (rho) é a densidade do fluido.
Temos a massa, agora para voltarmos à segunda lei de Newton precisamos da aceleração. Isso é exactamente o resultado da derivada do tempo do vector de velocidade.

Agora, tudo o que nos resta são os termos do lado direito do sinal de igual, e esses representam todas as forças que são aplicadas ao fluido.
O primeiro termo ∇p é o gradiente da pressão. Ele representa a diferença de pressão no espaço onde o fluido é contido. Por exemplo, se houver uma zona com baixa pressão e outra com pressão mais alta, o fluido se moverá da seção de alta pressão para a de baixa pressão. O gradiente de p está dizendo tudo isso.
O segundo termo descreve a viscosidade do fluido. Pense em dois líquidos diferentes, como a água e o mel. Quando você derrama um copo de água ele cai rápida e facilmente. Quando você faz a mesma coisa com o mel, ele fica pegajoso e derrama muito lentamente. Isto é o que essa expressão está dizendo.
O último termo, F, é o mais fácil porque representa todas as forças externas que podem ser aplicadas a esse fluido. Normalmente, a força que consideramos aqui é a gravidade.
É isto, todos aqueles símbolos extravagantes e letra média é apenas força = massa x aceleração.
Uso das equações Navier-Stokes
Desde que a resolução destas equações é tão complicada, para as usar temos de fazer muitas aproximações. Alguns exemplos são o fluxo Poiseuille e Couette. Com muitas suposições, estes dois cientistas foram capazes de encontrar uma solução para as equações de Navier-Stokes para uma aplicação muito específica. Entretanto, se quisermos usá-las para uma tarefa mais complicada, como as previsões meteorológicas, precisamos fazer algo mais.
A forma mais comum de usar essas equações é transformando-as, com a média de Reynolds. Este é um processo matemático avançado e os resultados são as equações de Reynolds. Elas são normalmente chamadas de equações RANS (que significa a média de Reynolds de Navier-Stokes).
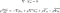
Estas equações são usadas quando o fluido está em um fluxo turbulento. Elas se parecem quase exatamente com as equações de Navier-Stokes, exceto pelo último termo. Isto é chamado de tensor de tensão Reynolds. É a quantidade que nos permite contabilizar a turbulência no fluido.
Nas equações RANS, as quantidades que utilizamos são calculadas como média num intervalo de tempo. Este intervalo tem de ser suficientemente pequeno para permitir a observação do fenómeno que estamos a estudar. Ao mesmo tempo, ele tem que ser grande o suficiente para fazer o efeito da turbulência perder importância.
Com as suposições certas, estas equações funcionam. Sabemos como usá-las para fazer os carros F1 mais rápidos, para fazer uma nave espacial ir para o ISS, e para fazer a previsão do tempo. Então você pode estar se perguntando porque a prova destas equações vale um milhão de dólares?
Um prêmio de um milhão de dólares
Do ponto de vista da física, estas equações são apenas a segunda lei de Newton que funciona com fluidos. Quando fazemos algumas suposições e algumas simplificações, podemos fazer coisas incríveis com elas.
O verdadeiro problema é este. Resolver estas equações sem aproximações é simplesmente terrivelmente complicado. É tão difícil que ainda não foi provado que as soluções realmente existem. E é aqui que entra o Prémio Millennium.
A afirmação oficial do problema (encontre-a aqui) é:
Prove ou dê um contra-exemplo da seguinte afirmação: em três dimensões espaciais e tempo, dado um campo de velocidade inicial, existe uma velocidade vectorial e um campo de pressão escalar, que são simultaneamente suaves e globalmente definidos, que resolvem as equações Navier-Stokes.
O que isto significa é que para ganhar o prémio tem de fazer três coisas:
- Provar que existe uma solução
- A solução tem de existir em cada ponto do espaço
- A solução tem de ser suave. Isto significa que uma pequena mudança nas condições iniciais produz apenas uma pequena variação do resultado.
Para um engenheiro é normalmente suficiente para saber que estas equações funcionam, mesmo que apenas a algum nível de aproximação. No entanto, para um matemático é muito importante saber se as soluções existem e como se comportam.
Você pode agora estar pensando que se elas funcionam como estão, gastar tempo e energia procurando uma prova é uma total perda de tempo. Bem, como muitos avanços tecnológicos na história da humanidade, o resultado pode não parecer muito importante. O importante é o caminho para chegar lá, que pode trazer novos conhecimentos e melhorias para a nossa vida.
Pense em missões espaciais. Se os humanos nunca decidissem ir e andar na lua não teríamos muitos objectos que são usados para melhorar a nossa vida. Máquinas de ressonância magnética e marcapassos vêm de tecnologias desenvolvidas para exploração espacial. Hoje os médicos de todo o mundo utilizam-nas todos os dias para salvar vidas. A mesma coisa se aplica aqui. O caminho para descobrir a solução para as equações Navier-Stokes irá ajudar-nos a melhorar a nossa compreensão dos fluidos e muito mais. Pode levar-nos a novas descobertas e provavelmente irá requerer a invenção de novas matemáticas. Isto pode então ser usado para responder a muitos outros problemas, para inventar novas tecnologias para melhorar as nossas vidas e tornar-nos melhores.