Podemos usar Gibbs-Helmholtz para obter a dependência da temperatura de \\(K\)
}{∂T} \Certo)_P = {-Δ_rH^o}{T^2}]
Em equilíbrio, podemos equacionar { Δ_rG^o} a {RTln K}} para obter:
>15}{∂T} \Certo)_P = |dfrac{Δ_rH^o}{RT^2}
Vemos que o aumento ou diminuição da temperatura está ligado ao facto de a entalpia da reacção ser positiva ou negativa. Se a temperatura mudar pouco o suficiente para que a \\(Δ_rH^o\) possa ser considerada constante, podemos traduzir um valor a uma temperatura para outra integrando a expressão acima, obtemos uma derivação semelhante à da depressão do ponto de fusão:
Se for necessária mais precisão, podemos corrigir as mudanças de temperatura de ΔrHo usando os dados da capacidade térmica.
Como \(K\) aumenta ou diminui com a temperatura está ligado ao facto de a entalpia de reacção ser positiva ou negativa.
A expressão para \(K\) é uma função bastante sensível da temperatura dada a sua dependência exponencial da diferença dos coeficientes estequiométricos Uma forma de ver a dependência sensível da temperatura das constantes de equilíbrio é lembrar que
No entanto, já que sob pressão e temperatura constantes
Equação \\\(\ref{18}}) torna-se
>
Tomando o log natural de ambos os lados, obtemos uma relação linear entre \(n K\ K\) e as entalpias e entropia padrão:
que é conhecida como a equação de Van’t Hoff. Ela mostra que uma trama de {\i1}(n K\i} vs. {\i}(1/T\i}) deve ser uma linha com declive {\i}(-Delta_r{H^o}/R\i} e interceptar {\i}(Delta_r{S^o}/R\i}.
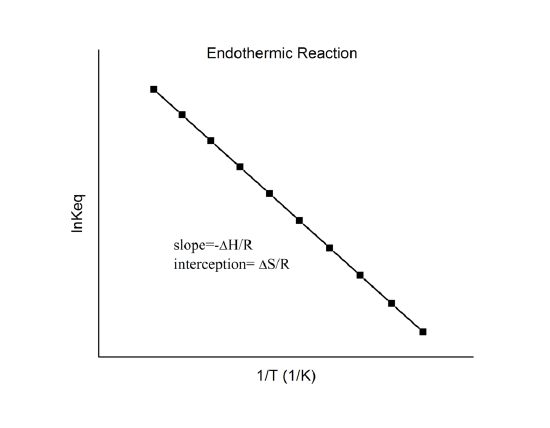
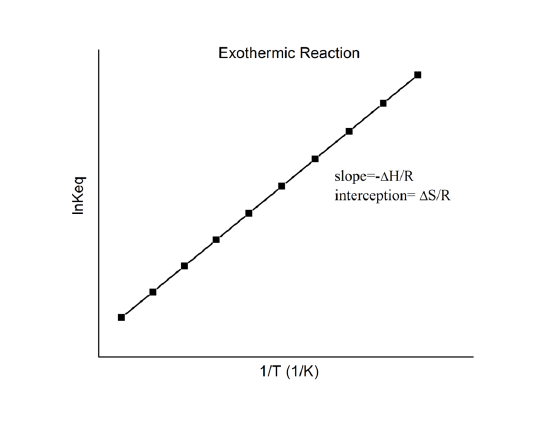
Hence, estas quantidades podem ser determinadas a partir dos dados {\ K} vs. 1/T sem fazer calorimetria. Naturalmente, a principal suposição aqui é que o Delta_r{H^o} e o Delta_r{S^o} são apenas muito fracamente dependentes do T, que é normalmente válido.