Álgebra Matrix

Descreveremos três exemplos das ciências da vida: um da física, um relacionado à genética, e um de um experimento com o mouse. Eles são muito diferentes, mas acabamos usando a mesma técnica estatística: modelos lineares adequados. Os modelos lineares são tipicamente ensinados e descritos na linguagem da álgebra matricial.

Exemplos de motivação

Queda de objetos

Imagine que você é Galileu no século 16 tentando descrever a velocidade de um objeto em queda. Um assistente sobe a Torre de Pisa e deixa cair uma bola, enquanto vários outros assistentes registam a posição em alturas diferentes. Vamos simular alguns dados usando as equações que conhecemos hoje e adicionando algum erro de medida:

set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##meters

Os assistentes entregam os dados a Galileu e é isto que ele vê:

mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")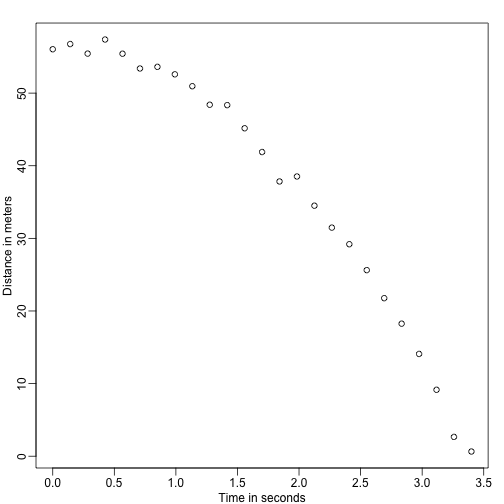

Ele não sabe a equação exacta, mas ao olhar para o gráfico acima ele deduz que a posição deve seguir uma parábola. Então ele modela os dados com:

Com a representação da localização, representando o tempo, e contabilizando o erro de medida. Este é um modelo linear porque é uma combinação linear de quantidades conhecidas (th s) referidas como preditores ou covariáveis e parâmetros desconhecidos (os s).

Pai &altura dos filhos

Agora imagine que você é Francis Galton no século 19 e você coleta dados de altura pareados de pais e filhos. Você suspeita que a altura é herdada. Os seus dados:

library(UsingR)x=father.son$fheighty=father.son$sheight

>

>

>

>

>

>

>

>

As alturas dos filhos parecem aumentar linearmente com as alturas dos pais. Neste caso, um modelo que descreve os dados é o seguinte:

Este também é um modelo linear com e , as alturas do pai e do filho respectivamente, para o -ésimo par e um termo para explicar a variabilidade extra. Aqui pensamos nas alturas do pai como o preditor e sendo fixo (não aleatório), por isso usamos letras minúsculas. O erro de medida por si só não pode explicar toda a variabilidade vista em . Isto faz sentido pois existem outras variáveis não no modelo, por exemplo, as alturas das mães, aleatoriedade genética e fatores ambientais.

Amostras aleatórias de múltiplas populações

Aqui lemos dados de peso corporal de ratos que foram alimentados com duas dietas diferentes: gordura alta e controle (chow). Temos uma amostra aleatória de 12 ratos para cada um. Estamos interessados em determinar se a dieta tem um efeito sobre o peso. Aqui estão os dados:

dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")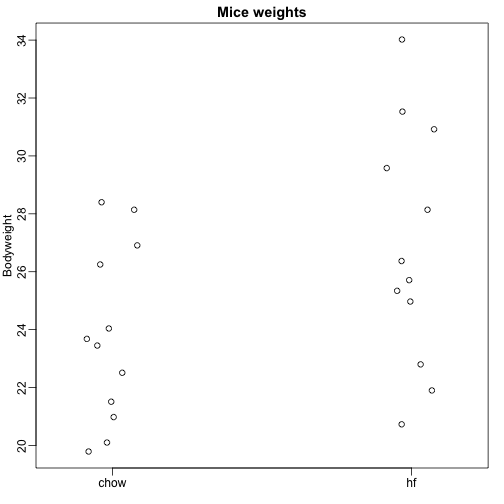

Queremos estimar a diferença de peso médio entre as populações. Nós demonstramos como fazer isso usando testes t e intervalos de confiança, com base na diferença nas médias das amostras. Podemos obter os mesmos resultados exatos usando um modelo linear:

com o peso médio da dieta da vaca, a diferença entre as médias, quando o mouse recebe a dieta de gordura alta (hf), quando recebe a dieta da vaca, e explica as diferenças entre ratos da mesma população.

Modelos lineares em geral

Vimos três exemplos muito diferentes nos quais os modelos lineares podem ser usados. Um modelo geral que engloba todos os exemplos acima é o seguinte:

Nota que temos um número geral de preditores . A álgebra matricial fornece uma linguagem compacta e uma estrutura matemática para computar e fazer derivações com qualquer modelo linear que se encaixe na estrutura acima.

Parâmetros de estimulação

Para que os modelos acima sejam úteis, temos que estimar os s desconhecidos. No segundo exemplo, entendemos melhor a herança, estimando o quanto, em média, a altura do pai afeta a altura do filho. No exemplo final, queremos determinar se existe de fato uma diferença: se .

A abordagem padrão em ciência é encontrar os valores que minimizem a distância do modelo ajustado aos dados. O seguinte é chamado de equação dos mínimos quadrados (LS) e vamos vê-la frequentemente neste capítulo:

Após encontrarmos o mínimo, vamos chamar aos valores os mínimos quadrados estimados (LSE) e denotá-los com . A quantidade obtida ao avaliar a equação dos mínimos quadrados nas estimativas é chamada de soma residual dos quadrados (RSS). Como todas estas quantidades dependem de , são variáveis aleatórias. As s são variáveis aleatórias e eventualmente faremos inferências sobre elas.

Exemplo de objeto em queda revisitado

Pois do meu professor de física do ensino médio, sei que a equação para a trajetória de um objeto em queda é:

com e a altura e a velocidade inicial respectivamente. Os dados que simulamos acima seguiram esta equação e adicionaram erro de medida para simular n observações para a queda da bola da torre de Pisa . Por isso utilizamos este código para simular dados:

g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)

Aqui está o aspecto dos dados com a linha sólida representando a verdadeira trajetória:

plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)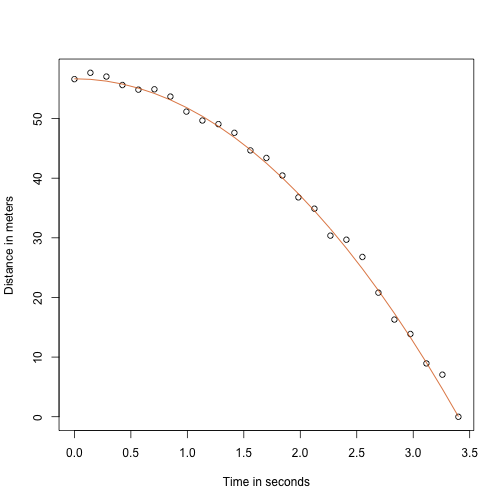

Mas estávamos fingindo ser Galileu e por isso não conhecemos os parâmetros do modelo. Os dados sugerem que é uma parábola, então nós a modelamos como tal:

Como encontramos o LSE?

A função lm

Em R podemos encaixar este modelo simplesmente usando a função lm. Descreveremos esta função em detalhe mais tarde, mas aqui está uma pré-visualização:

tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef

## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17

Dispõe-nos o LSE, bem como os erros padrão e os valores p.

Parte do que fazemos nesta secção é explicar a matemática por detrás desta função.

A estimativa dos mínimos quadrados (LSE)

Vamos escrever uma função que computa o RSS para qualquer vector :

rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}

Então, para qualquer vector tridimensional, obtemos um RSS. Aqui está um gráfico do RSS em função de quando mantemos os outros dois fixos:

Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)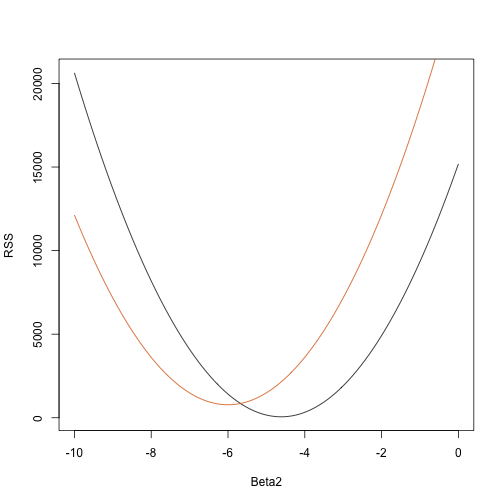

Trial e o erro aqui não vai funcionar. Em vez disso, podemos usar o cálculo: pegue as derivadas parciais, coloque-as em 0 e resolva. Claro que, se tivermos muitos parâmetros, estas equações podem ficar bastante complexas. Álgebra linear fornece uma forma compacta e geral de resolver este problema.

Mais sobre Galton (Avançado)

Ao estudar os dados pai-filho, Galton fez uma descoberta fascinante usando análise exploratória.

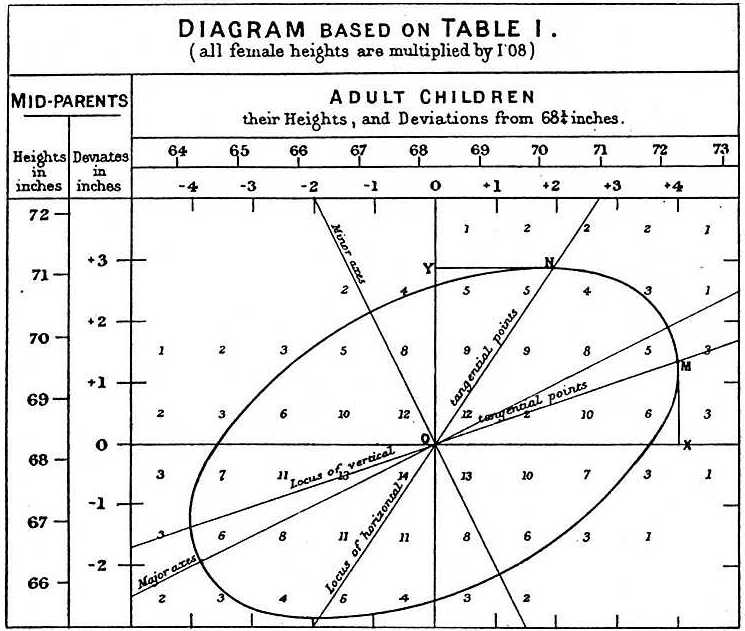
Ele notou que se ele tabulou o número de pares de altura pai-filho e seguiu todos os valores x,y tendo os mesmos totais na tabela, eles formaram uma elipse. No gráfico acima, feito por Galton, você vê a elipse formada pelos pares que têm 3 caixas. Isto levou então a modelar estes dados como normal bivariada correlacionada que descrevemos anteriormente:

Descrevemos como podemos usar a matemática para mostrar que se você mantém fixa (condição a ser ) a distribuição de é normalmente distribuída com média: e desvio padrão . Note que esta é a correlação entre e , o que implica que se fixarmos , de facto segue um modelo linear. Os e parâmetros do nosso modelo linear simples podem ser expressos em termos de , e .