Wprowadzenie do butelki Kleina

Jeśli lubisz pić, to butelka Kleina nie jest zalecanym naczyniem. Może i wygląda jak butelka, ale nie zamyka w sobie żadnej objętości, co oznacza, że nie może pomieścić żadnego płynu. Cokolwiek wlejesz „do środka” po prostu wypłynie z powrotem.

Jak skonstruować taką dziwną rzecz i dlaczego chciałbyś ją skonstruować? Matematyk Felix Klein, który odkrył butelkę w 1882 roku, opisał ją jako powierzchnię, która „może być zwizualizowana poprzez odwrócenie kawałka gumowej rurki i przepuszczenie jej przez siebie tak, że zewnętrzna i wewnętrzna część spotykają się”.

Twoja przeglądarka nie obsługuje tagu video.Link bezpośredni

Jest oczywiste, że butelka Kleina, podobnie jak bardziej znana kula, jest powierzchnią zamkniętą: jest skończona w tym sensie, że można ją zmieścić w skończonym obszarze przestrzeni, ale mrówka mogłaby chodzić po niej w nieskończoność, nigdy nie napotykając granicy ani nie wypadając poza krawędź. W przeciwieństwie do kuli, która ma wnętrze i zewnętrze, butelka Kleina jest jednostronna: chodząc dookoła, nasza mrówka mogłaby dotrzeć do obu stron każdego punktu powierzchni. To właśnie dlatego butelka nie zawiera żadnej objętości, a także odpowiada na pytanie „dlaczego”: butelka Kleina jest interesująca, ponieważ w przyrodzie nie spotykamy wielu jednostronnych kształtów. (Zobacz tutaj inny bardzo ładny obrazek butelki Kleina.)

Pasek Möbiusa jest jednostronny – zobacz wersję animowaną. (Obraz i animacja autorstwa Konrada Polthiera.)

Jeśli to jest trochę mylące, pomyśl o prostszym przykładzie jednostronnej powierzchni: słynnym pasku Möbiusa. Można go zrobić, biorąc dwa końce paska papieru, skręcając go, a następnie sklejając końce razem. Używając paska papieru, którego dwie strony mają różne kolory, na przykład zielony i pomarańczowy, łatwo przekonać się, że powstały w ten sposób pasek Möbiusa jest jednostronny. Kiedy już skręcisz i skleisz, przekonasz się, że możesz dotrzeć do każdego pomarańczowego punktu z każdego zielonego punktu bez konieczności przebijania się przez papier lub wspinania się po jego krawędzi.

W przeciwieństwie do butelki Kleina, pasek Möbiusa ma granicę – składa się ona z dwóch nieprzyklejonych krawędzi oryginalnego paska. Ale istnieje związek między nimi. Jeśli weźmiemy dwa paski Möbiusa i stworzymy zamknięty kształt poprzez połączenie ich granic za pomocą zwykłego paska dwustronnego, jak pokazano poniżej, to otrzymamy dokładnie butelkę Kleina.

Twoja przeglądarka nie obsługuje znacznika video.Link bezpośredni

Fakt ten zainspirował matematyka Leo Mosera do skomponowania limeryku:

Matematyk o nazwisku KleinMyślał, że wstęga Möbiusa jest boska.Powiedział: „If you glueThe edges of two,You’ll get a weird bottle like mine.”

Niektórzy matematycy naprawdę są wszechstronnie utalentowani!

Inną ciekawą cechą butelki Kleina jest to, że przecina ona samą siebie, co oznacza, że trudno ją zrobić z pojedynczej rurki gumy, jak sugerował Klein. Ściśle mówiąc, samo przecinający się obiekt przedstawiony powyżej nie jest butelką Kleina, ale (jak wskazał Klein) jedynie wizualizacją butelki. Aby zrozumieć dlaczego, pomyślmy najpierw o bardziej znanym pączku (znanym matematycznie jako torus). Możesz zrobić torus z kwadratowego arkusza gumy, najpierw sklejając dwa przeciwległe boki, aby utworzyć cylinder, a następnie sklejając dwa elementy brzegowe tego cylindra, aby uzyskać torus.

Robiąc torus: Najpierw sklej przeciwległe punkty na dwóch przeciwległych bokach kwadratu, aby utworzyć walec, a następnie sklej dwa okręgi graniczne tego walca (odpowiadające sklejeniu przeciwległych punktów na pozostałych dwóch bokach kwadratu), aby utworzyć torus.

Jeśli nie chcesz zawracać sobie głowy sklejaniem, możesz po prostu myśleć o torusie jak o kwadracie, pamiętając, że przeciwległe punkty na przeciwległych bokach są uważane za takie same. Więc kiedy przesuniesz kształt narysowany na „kwadracie” przez górną krawędź, pojawi się on ponownie na dolnej krawędzi, a kiedy przesuniesz go przez prawą krawędź, pojawi się on ponownie na lewej krawędzi (i vice versa).

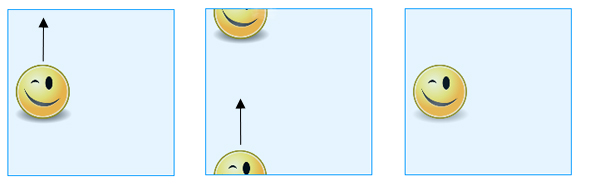
Gdy przesuniesz kształt narysowany na „kwadracie” przez górną krawędź, pojawi się on ponownie na dolnej krawędzi.

Aby otrzymać prawdziwą butelkę Kleina, zacznij w ten sam sposób, identyfikując przeciwległe punkty na parze przeciwległych boków kwadratu. Dla drugiej pary boków, jednak, nie zidentyfikować punkty, które są bezpośrednio przeciwległe, ale punkty, które są ukośnie przeciwległe, jak pokazano na rysunku.

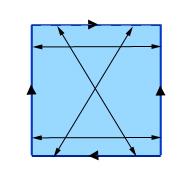
Robiąc butelkę Kleina: zidentyfikuj przeciwległe punkty dwóch przeciwległych boków (pionowe na tym rysunku), a następnie zidentyfikuj punkty ukośnie przeciwległe na pozostałych dwóch bokach. (Jeśli oznaczymy punkty na górnej i dolnej stronie od lewej do prawej przez liczby od 0 do 1, to punkt z etykietą x na górnej stronie jest identyfikowany z punktem z etykietą 1-x na dolnej stronie.)

Powstały obiekt to butelka Kleina. Ponownie, możesz myśleć o niej jak o kwadracie, pamiętając, które punkty graniczne są uważane za takie same. Jeśli przesuniesz kształt nad jedną z krawędzi, która miała zidentyfikowane przeciwległe punkty (pionowe na naszym obrazku), pojawia się on ponownie po przeciwnej stronie, tak jak poprzednio. Jeśli jednak przesuniemy go po jednej z krawędzi, której punkty zostały zidentyfikowane po przekątnej (poziomo na naszym rysunku), pojawia się po przeciwnej stronie, ale przesunięty i jako lustrzane odbicie swojego pierwotnego ja.

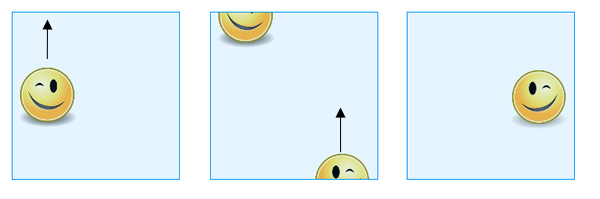
Jeśli przesuniesz kształt przez górną krawędź, pojawia się on w poprzek dolnej krawędzi, ale na drugą stronę i jako lustrzane odbicie swojego pierwotnego ja.

Jedynym sposobem na zbudowanie tego kształtu w przestrzeni trójwymiarowej poprzez rzeczywiste sklejenie punktów jest pozwolenie mu na przecięcie się. To sprowadza się do identyfikacji par punktów we wnętrzu oryginalnego kwadratu, więc ściśle mówiąc, wynikowy kształt nie jest dokładnie taki sam jak butelka Kleina, która ma tylko zidentyfikowane punkty graniczne. Jest to tylko jeden ze sposobów reprezentowania butelki w przestrzeni trójwymiarowej (są też inne).

Zaskakujące jest to, że pojęcia „wewnątrz”, „na zewnątrz” i „jednostronności” zależą od przestrzeni otoczenia, w której znajduje się obiekt. Na przykład pętla narysowana na kartce papieru (w przestrzeni dwuwymiarowej) ma dobrze zdefiniowane wnętrze i zewnętrze, ale pętla narysowana w przestrzeni trójwymiarowej już nie. Dlatego nie możemy mówić o jednostronności, jeśli najpierw nie zdecydujemy, jak osadzić powierzchnię w przestrzeni trójwymiarowej. Istnieje jednak pewna ściśle związana z tym własność, która jest nieodłączną cechą kształtu i nie zależy od otaczającej go przestrzeni. Powierzchnię nazywamy orientowalną, jeśli nie można przesunąć narysowanego na niej kształtu dookoła i z powrotem do miejsca, w którym się zaczął, tak że wygląda jak swoje lustrzane odbicie. Jak widać na animacji towarzyszącej obrazkowi po prawej stronie, pasek Möbiusa nie jest orientowalny. I jak widać na obrazku z uśmiechniętą buźką powyżej, butelka Kleina też nie jest. Aby dać jej pełny matematyczny opis, butelka Kleina jest zamkniętą, nieorientowalną powierzchnią. Aby dowiedzieć się więcej na ten temat zobacz artykuł Wewnątrz butelki Kleina.

O autorce

Marianne Freiberger jest redaktorką czasopisma Plus.

.